А.Ш. Кажикенова, Д.Б. Алибиев, Шегирова Д.К., А.Б.Сейтимбетова

Карагандинский государственный университет им. Е.А. Букетова

Вязкость германия на основе кластерно-ассоциатной модели

Многие авторы при изучении жидкого металлического состояния среди большого разнообразия моделей жидкости отдают предпочтение тем, которые опираются на концепцию квазикристаллического описания. Такой подход базируется на единстве конденсированного состояния вещества, единстве сил межчастичного притяжения по обе стороны интервала плавления.

Методы расчета вязкости жидких металлов, основанные на модельных теориях, псевдопотенциальной теории, на дифракционных исследованиях, статистической геометрии многогранников Вороного, позволили накопить огромный экспериментальных материал по свойствам и структуре жидких металлов. Однако все эти модели также допускают часто необоснованные приближения, работают в узком диапазоне температур. Данные по вязкости, полученные различными исследованиями или расчетом по различным теориям, порой отличаются на несколько порядков. Все это указывает на необходимость дополнительных разработок на основе альтернативных подходов к пониманию вязкости.

Как уже ранее отмечалось, сотрудники Химико-металлургического института им. Ж. Абишева (г.Караганда) разработали новую концепцию хаотизированных частиц [1], основанный на распределении Больцмана. Согласно концепции, три агрегатных состояния вещества рассматриваются с единой точки зрения по его бесструктурной составляющей. По концепции хаотизированных частиц в каждом из трех агрегатных состояний присутствуют кристаллоподвижные, жидкоподвижные и пароподвижные частицы.

Авторами [1] на основе концепции хаотизированных частиц были предложены три модели вязкости жидких металлов:

- с учетом только кристаллоподвижных частиц

n , (1)

- с учетом кристаллоподвижных и жидкоподвижных частиц

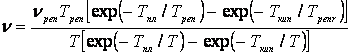, (2)

- с учетом всех трех видов частиц

n 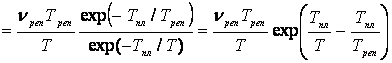, (3)

где n_реп и T_реп – соответственно кинематическая вязкость и абсолютная температура для некоторой реперной точки (наиболее надежное экспериментальное значение); T_пл и T_кип – соответственно температура плавления и кипения.

Применение предложенных моделей затруднено тем, что необходимо проверять каждую модель и затем выбирать из них наиболее адекватную. В ходе проверки было установлено, что на сильную зависимость вязкости от температуры большое влияние оказывает образование ассоциированных кластеров, разрушение которых с повышением температуры происходит параллельно с разрушением элементарных кластеров. Поэтому мы считаем, что в модели (1) надо усилить фрагмент путем возведения его в степень, равную числу соударяющихся кластеров

(4)

где показатель a - степень ассоциации`п-частичных кластеров.

Полученное среднее значение мы проверили на представительность по критерию однородности множества и затем использовали в уравнении (4) для получения расчетных значений и сравнения с экспериментальными по коэффициенту корреляции.

Покажем применимость предлагаемых моделей на примере расчета вязкости германия. Для германия в справочнике [2] приводятся T_пл = 1211,41 К, T_кип = 3120 К, а также данные по кинематической вязкости. Эти данные сравнили с рассчитанными по моделям (1)-(4). Результаты сравнения приведены в таблице и на рисунке. За реперную взяли точку близкую к точке плавления T_реп = 1218 К и n_реп = 1,35×10^-7 м²/с.

Таблица – Сопоставление экспериментальных [2] и рассчитанных по моделям (1)-(4) данных по кинематической вязкости германия, n ×10⁷, м²/с

T	ν(эксп)	ν(1)	ν(2)	ν(3)	a	ν(4)
Tпл=1211,41	-	1,36	1,36	1,36	-	1,37
1218	1,35	1,35	1,35	1,35	-	1,35
1233	1,31	1,33	1,32	1,32	2,46	1,30
1243	1,24	1,32	1,31	1,30	4,18	1,28
1251	1,22	1,31	1,29	1,28	3,79	1,25
1268	1,19	1,30	1,27	1,25	3,14	1,21
1283	1,16	1,28	1,25	1,22	2,92	1,17
1363	1,06	1,21	1,14	1,09	2,15	0,98
1403	1,01	1,17	1,09	1,03	2,05	0,91
1458	0,98	1,13	1,04	0,96	1,78	0,81
Tкип =3120	-	0,53	0,50	0,29	-	0,10

Как видно из таблицы и рисунка, более точными по описанию температурной зависимости являются модели (3) и (4). Коэффициенты корреляции для модели (3) и обобщенной (4) приблизительно равны, поэтому достаточно для расчета вязкости применить модель более общего вида.

Среднее значение ā = 2,81. Однородность полученного множества для а по критерию Налимова соблюдается: S(x) = 0,858; = 1,714 < r_cr = 2,073. С учетом степени ассоциированности кластеров в качестве обобщенной модели вязкости расплавов в полном диапазоне температур можно использовать модель (4) по кинематической вязкости германия с нахождением доверительного интервала и с округлением

м²/с.

T_m

4

3

2

1

T, K

n×10⁷, м²/с

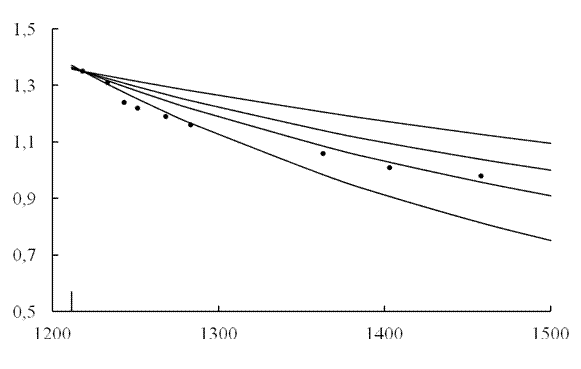
n - кинематическая вязкость, Т – температура.

Точки – экспериментальные данные [2], 1 – по модели (1),

2 – по (2), 3 – по (3), 4 – по (4)

Рисунок – Зависимость кинематической вязкости германия от температуры

Предлагаемая кластерно-ассоциатная модель была проверена на 28 металлах, для которых имеются справочные данные по вязкости. В большинстве случаев модель (4) была наиболее адекватной в сравнении с моделями (1)-(3).

Литература

1. Малышев В.П., Турдукожаева А.М., Кажикенова А.Ш. Вязкость расплавов металлов по концепции хаотизированных частиц // Тяжелое машиностроение. – 2009. – № 6. – С. 37-39.

2. Свойства элементов: Справ. изд. – В 2 кн. Кн. 1 // Под ред. Дрица М. Е. – 3-е изд., перераб. и доп. – М.: Изд. дом «Руда и Металлы», 2003. –448 с.