Физика /1.Теоретическая физика
К.п.н. Мищик С.А.
Государственный морской университет имени
адмирала Ф.Ф.Ушакова ,
Россия
Системные волновые задачи
прикладной физики морского флота
Системные волновые задачи прикладной
физики морского флота отражают целостно-системное моделирование основных
элементов транспортных объектов. При этом возникает ориентация на единство
базисных характеристик предметных и исполнительных условий относительно
предмета содержания и способа его реализации. Рассматриваются: кинематические и динамические параметры волновых
процессов морских волн, морских плавсредств и их элементов при морском волнении и изменяющейся внешней среды с расчётами амплитудных,
временных, динамических и кинематических параметров составляющих элементов
транспортных морских систем, отражающих
функциональную пространственно-временную зависимость управления на морском флоте.
В процессе решения системных волновых
задач прикладной физики морского флота необходимо применять основные положения
теории деятельности, системного анализа и теории формирования интеллекта.
Системный анализ предполагает
выполнение последовательности системных аналитических действий: выделить объект
анализа – волновую задачу прикладной физики морского флота (ВЗПФМФ) как
систему; установить порождающую среду ВЗПФМФ; определить уровни анализа ВЗПФМФ;
представить целостные свойства ВЗПФМФ относительно пространственных, и временных
характеристик и их комбинаций; выделить структуру уровня анализа ВЗПФМФ;
установить структурные элементы уровня анализа ВЗПФМФ; определить
системообразующие связи данного уровня анализа ВЗПФМФ; представить межуровневые
связи анализа ВЗПФМФ; выделить форму организации ВЗПФМФ; установить системные
свойства и поведение ВЗПФМФ.
Задача 1
В океанах длина волны достигает 300 метров, а период волны
13,5 секунд. Определить скорость распространения океанских волн.
Ответ: υ = 22,2 м/с .
Задача 2
Ял-6 качается на морских волнах, распространяющихся со
скоростью υ = 2,5 м/с. Расстояние между двумя ближайшими гребнями морских
волн 8 метров. Определить период колебания Яла-6.
Ответ: Т=3,2 с .
Задача 3
Вахтенный штурман во время стоянки определил, что
расстояние между следующими друг за другом гребнями морских волн равно 8 метров
и за 60 секунд мимо него прошло 23 волновых гребня. Определить скорость
распространения морской волны.
Ответ: υ = 2,9 м/с .
Задача 4
Расстояние между гребнями волн на море 5 метров. При
встречном движении катера волна за одну секунду ударяется о корпус катера 4
раза, а при попутном – 2 раза. Определить скорости морской волны и катера, если
скорость катера больше скорости морской волны.
Ответ: υк = 15 м/с ; υв
= 5 м/с .
Задача 5
При сбрасывании с судна шлюпки в морском заливе в
безветренную погоду от места бросания пошли волны. Матрос, стоящий на берегу,
заметил, что волна дошла до него через 50 секунд, расстояние между соседними
горбами морских волн 0,5 метра и за 5 секунд было 20 всплесков о берег.
Определить расстояние между судном и берегом.
Ответ: S=100 метров.
Задача 6
Морской спасатель определил, что за 10 секунд
спасательный плот совершил на волнах 20 колебаний, а расстояние между соседними
гребнями морских волн равно 1,2 метра. Рассчитать скорость распространения морских
волн.
Ответ:
υ = 2,4 м/с .
Задача 7
Узкий пучок ультразвуковых волн частотой vo=50 кГц
направлен от неподвижного локатора к приближающейся подводной лодке. Определить
скорость U подводной лодки, если частота v1 биений
(разность частот колебаний источника и сигнала, отраженного от лодки) равна 250
Гц. Скорость υ ультразвука
в морской воде принять равной 1,5 км/с.
Ответ: U = 3,74 м/с .
Задача 8
Найти уравнение стоячей волны и спектр собственных
частот в натянутом швартовном тросе длиной ℓ, один из концов которого закреплен на причальной
тумбе, а второй – на морском судне. Плотность швартовного троса ρ,
модуль Юнга Е .
Ответ:
![]() ;
;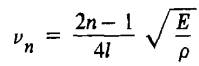 .
.
Задача 9
Найти энергию упругой стоячей волны в натянутом
швартовном тросе массой m, один
из концов которого закреплен на причальной тумбе, если на втором конце – на
морском судне созданы колебания с собственной частотой vn
и амплитудой а .
Ответ:
![]() .
.
Задача 10
Плоская морская волна ξ
= a·cos(ωt - kz)
распространяется в прибрежной среде плотностью ρ. Определить средний за период колебаний поток энергии
плоской волны действующей на часть поверхности в форме полусферы, задаваемой
уравнением z = ![]() , отшвартованного морского судна.
, отшвартованного морского судна.
Ответ:
<Ф>
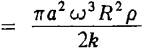 .
.
Задача 11
В натянутом швартовном тросе длиной ℓ и
массой m установилась стоячая волна вида ξ = a·cos(kх)·cos(ωt). Определить энергию упругих колебаний, заключенную
между соседними узлами смещения в натянутом швартовном тросе.
Ответ:
![]() .
.
Задача 12
От носа морского судна, идущего по тихой воде моря со
скоростью V = 20 узлов (1 узел равен 0,5 м/с), бежит волна, образующая угол φ =
20° с направлением движения морского судна. С какой скоростью υ распространяется
морская волна?
Ответ:
υ = 3,42 м/с .
Задача 13
Концы морской судовой антенны в виде длинного провода,
натянуты силой F = 400 Н, закреплены между мачтами на расстоянии ℓ = 20 м друг
от друга. Поперечное возмущение ветровой нагрузки распространяется от одного
закрепленного конца морской судовой антенны до другого за время t =
0,5 с. Определить полную массу m морской судовой антенны.
Ответ:
m = 5 кг.
Задача 14
Плоская волна уравнения вида ξ = a·sin(ωt - kх) распространяется в морской среде с плотностью ρ
со скоростью V. Определить изменение давления ΔР в морской среде как функцию координаты х и
времени t.
Ответ: ΔР = ρ V a·cos(ωt - kх).
Задача 15
Швартовный трос свешивается вертикально с борта
морского судна и натянут собственным весом. Определите скорость поперечных волн
в швартовном тросе как функцию расстояния У от его нижнего конца.
Ответ: ![]() .
.
Задача 16
Судовой грузовой трос массы m закреплён на палубе с обоих сторон. Под действием ветра в тросе возникают
колебания с круговой частотой ω и максимальной амплитудой смещения aмакс .
Определить максимальную
кинетическую энергию и среднюю кинетическую энергию за период колебаний судового
грузового троса.
Ответ: Екмакс = m ω2 aмакс2/4; <Екмакс> = m ω2 aмакс2/8 .
Задача 17
В натянутом швартовном тросе плотностью ρ
установилась стоячая волна вида ξ =
a·cos(kх)·cos(ωt).
Определить в натянутом швартовном тросе выражения для объёмной плотности
потенциальной и кинетической энергии.
Ответ:
ωp = (ρω2a2/2) sin2(kх)·cos2(ωt); ωк = (ρω2a2/2)
cos2(kх)·sin2(ωt)
Задача 18
В натянутом швартовном тросе плотностью ρ и площадью поперечного сечения S установилась стоячая волна вида ξ = a·sin(kх)·cos(ωt). Определить в натянутом швартовном тросе полную
механическую энергию, заключённую между сечениями швартовного троса, которые
проходят через соседние узлы смещения.
Ответ: Емех = πρSω2a2/4k .
Задача 19
В морской среде распространяется незатухающая плоская
гармоническая волна. Определить среднюю объёмную плотность полной энергии
колебаний морской волны <ω>,
если через одну шестую периода
колебаний после прохождения максимума смещения морской поверхности в любой
точке морской среды объёмная плотность энергии равна ω0.
Ответ: <ω>=2/3
ω0 .
Задача 20
Морское судно движется движется против волны длиной λ = 100
метров с курсовым углом φ=150
и скоростью υs=17 узлов (1 узел равен 0,5 м/с). Определить кажущийся
период волнения.
Ответ:
τ0 = 4,8 с .
Задача 21
Морское судно движется движется по волнению, длина
волны которого λ = 149
метров, с курсовым углом φ=700.
Период бортовой качки τб =
16 секунд. Определить скорость движения судна, при которой возможен резонанс бортовой
качки.
Ответ: υ = 33,9 узла (1
узел равен 0,514 м/с).
Задача 22
Определить значение курсового угла к волне φ морского судна, идущего при осадке Т=3,76
метра со скоростью υ = 15 узлов
(1 узел равен 0,514 м/с), при котором морское судно будет испытывать
резонансную килевую качку на волнах длиной λ
= 80 метров.
Ответ: φ=460
.
Задача 23
При каких значениям длины морской волны λ волнение вызовет резонансную бортовую качку морского
судна, идущего против волны со скоростью υ = 9 узлов (1
узел равен 0,514 м/с), при курсовом угле φ=1500?
Судно имеет ширину B=10 метров, поперечную метацентрическую высоту h=0,48 метра. Коэффициент класса морского судна равен C=0,77.
Ответ: λ
= 188 метров.
Задача 24
Какие курсовые углы φ благоприятны
для танкера шириной B=44 метра,
идущего со скоростью υ = 15,5 узлов
(1 узел равен 0,514 м/с), при осадке Т=17 метров и поперечной метацентрической
высоте h=0,48 метров на волнах длиной λ = 160
метров? Коэффициент класса морского судна равен C=0,82.
Ответ: против
волны φ=640… 780
; по волне φ=00… 350
.
Задача 25
Морское судно идёт курсовым углом к волнам зыби φ=1620, длина морской волны λ = 50
метров. При какой скорости морского судна качка прекратится из-за бесконечно
большого значения кажущегося периода волны τ0 .
Ответ: υ = 18,5 узла (1 узел равен 0,514 м/с).
Задача 26
Определить, при какой длине морской волны λ, морское судно может безопасно лечь в дрейф, если ширина
судна B=14 метров и поперечная метацентрическая высота h=0,96 метра.
Ответ: λ
< 122 метра.
Задача 27
Определить дополнительный изгибающий момент в районе
миделя судна на вершине и подошве волны, если длина судна L = 50 метров, ширина судна B=5 метров,
высота волны h=0,17 L0,75 метра,
плотность воды ρ=1025 кг/м3,
коэффициент полноты ватерлинии α = 0,8 .
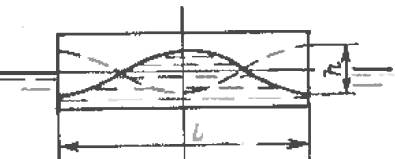
Ответ: δМв=5,6 кН·м;
δМп= - 6,45 кН·м.
Задача 28
Во сколько раз увеличится дополнительный изгибающий
момент от действия волны на миделе морского судна длиной L(метров),
если при постоянном водоизмещении увеличить длину судна в 1,2 раза и уменьшить
ширину в 1,2 раза. Коэффициент полноты ватерлинии α остаётся без
изменения. Высота волны h=0,17 L0,75 метра.
Ответ: в 1,376
раза.
Задача 29
При волнении моря 5 баллов промысловое судно массой Δо=2800 тонн на скорости υ = 0,5 м/с швартуется
к борту промысловой базы массой Δс=12000 тонн, имеющей кранцевую защиту. Определить
кинетическую энергию соударяемых судов, энергоёмкость одного кранца и значение
контактного давления.
Ответ: Ек = 383 кДж; А = 292 кДж; Рк = 1,97 кПа .
Задача 30
Определить высоту морской волны, при которой возможна
безопасная буксировка стальным буксирным тросом длиной L=600 метров, диаметром d=52 мм, если горизонтальная составляющая силы
натяжения Fг=98 кН, сила разрыва Рразр = 880 кН. Расстояние между судами на спокойной воде АВ = 595,2 метра, При этом Fг = То . Расстояние между судами при рывке А*В*
= 599,8 метра, и То = 0,5 Рразр .
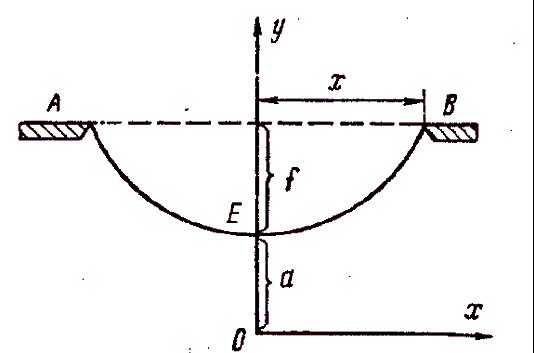
Ответ: h= 6,7 метра.
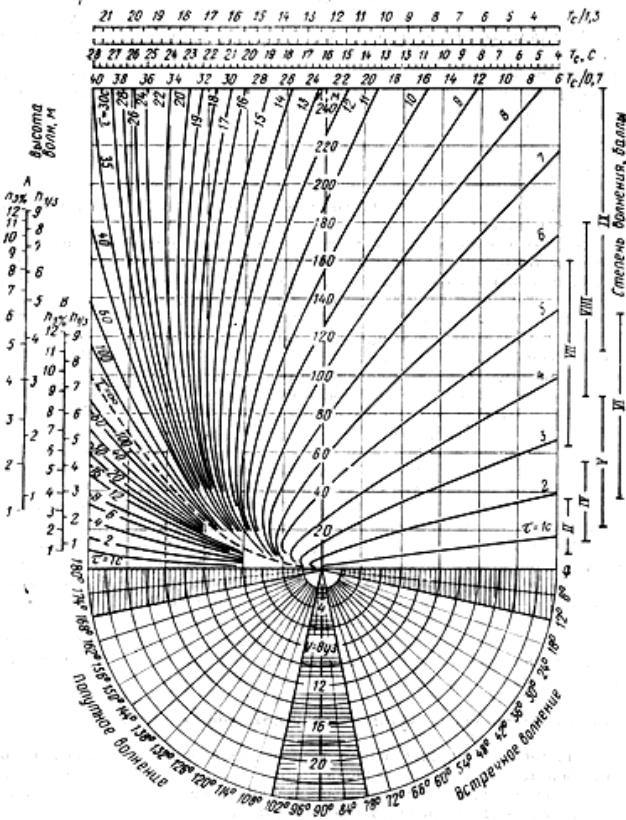
Штормовая
диаграмма Ю.В.Ремеза