К.т.н. Шмидт И.В., д.т.н. Дьяконов А.А.

ФГБОУ ВПО «ЮУрГУ» (НИУ), г. Челябинск, Россия

Математическая постановка задачи
напряженно-деформированного состояния
конструкционной композитной слоистой
системы при механической обработке резанием

Слоистые системы или детали с модифицированными слоями широко используются в машиностроении при обеспечении бесперебойной работы деталей и узлов, работающих в условиях повышенного износа и агрессивных средах. Принципиальным отличием слоистых систем от монолитных деталей является наличие слоев из различных материалов, нанесенных на основной материал конструкции. В последнее время находят широкое применение слоистые системы с полимерно-композитными материалами (ПКМ), при изготовлении которых применяются традиционные методы механической обработки – точение, шлифование.

Как известно из практики, нередко в процессе обработки слоистой системы при интенсивных режимах резания образуются дефекты типа отслоения или разрушения слоя [1]. Здесь сказывается различие свойств материалов, входящих в слоистую систему. Прочностные свойства ПКМ на порядок ниже, чем у традиционных конструкционных материалов [2]. Кроме того, существуют предельные силы сцепления между слоями. Каждый материал любого из слоев имеет свой максимально допустимый предел прочности (например, предел прочности на отрыв от стали слоя из ПКМ составляет 5…50 МПа), который будет влиять на назначение режимов резания при обработке слоистой системы.

Кроме того, деформационные свойства ПКМ значительно отличаются от свойств металлов. Такое различие предопределяет сложный характер напряженного состояния, возникающего от действия сил резания. Следовательно, актуальна задача анализа напряженного состояния системы в целом под действием сил резания.

Напряженное состояние слоистой системы с рабочим слоем из стали и средним слоем из ПКМ, нанесенных на основной элемент конструкции – вал, при круглом шлифовании с радиальной подачей рассматривалось в работе
В.А. Пашнева [3]. Для этого ставилась плоская двумерная контактная задача теории упругости для системы трех тел при внешней нагрузке. Такая постановка не учитывает схему закрепления детали на станке и осевую подачу.

В данной работе ставится общая задача моделирования напряженного состояния слоистой системы, состоящей из n слоев из различных материалов, схемы закрепления, уровня и схемы приложения нагрузок, соответствующих точению и шлифованию.

Как правило, слоистой системой представлена не вся деталь, а только ее часть, где необходимо получить свойства рабочей поверхности, отличающиеся от свойств материала основной конструкции. Поэтому, для упрощения расчетов рассматривается только часть конструкции – слоистая система из n слоев, а ее закрепление осуществляется по торцу основного элемента конструкции – вала (рис.1), имитирующей установку в патроне и по двум торцам основного элемента конструкции – вала, имитирующей установку в центрах. Действующие при обработке на слоистую систему силы прикладываются следующим образом: при точении (P_x, P_y, P_z) – точечно (рис. 1а); при шлифовании (P_y, P_z) – распределено по пятну контакта инструмента с заготовкой (рис. 1б).

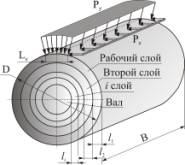
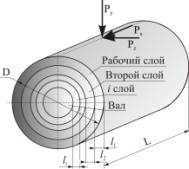
а) б)

Рис. 1. Схема нагружения слоистой системы:

а) при круглом врезном шлифовании; б) при продольном точении

Математическую постановку задачи теории упругости для схемы (рис. 1) целесообразнее производить в цилиндрических координатах, для этого используем расчетную схему (рис. 2).

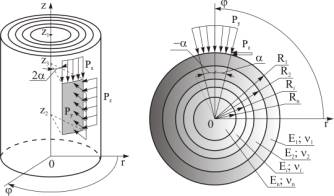
Рис. 2. Расчетная схема в цилиндрических координатах

Тогда уравнение равновесия в перемещениях при отсутствии массовых сил в цилиндрических координатах для расчетной схемы (рис. 2) примет вид:

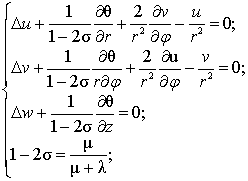
где Δ – оператор Лапласа; u, v, w – перемещения по направлениям r, φ, z соответственно; µ и λ – коэффициенты Ламе.

Закон Гука в цилиндрических координатах выглядит:

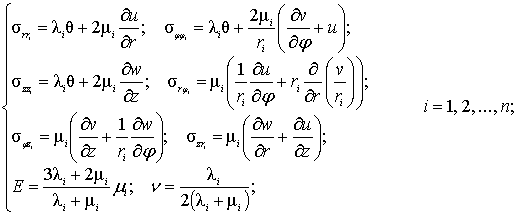
где Е – модуль Юнга; ν – коэффициент Пуассона.

Границы контактирующих тел описываются следующим образом: первое тело (рабочий слой системы) (i=1); n-ое тело (n-ый слой системы – вал) (i=n)

Граничные условия отражают приложенную нагрузку, условия контакта тел и условия закрепления.

Описание приложенной нагрузки сводится к заданию напряжений на внешней границе:

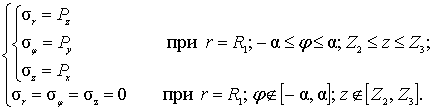
Условия сопряжения контактирующих тел задается в виде ограничения на перемещения:

контакт между первым и вторым телом (слоем)

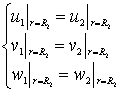i=1, 2, …, n;

контакт между (i-1)-ым и i-ым телом (слоем)

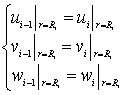i=1, 2, …, n.

Условие закрепления системы тел: .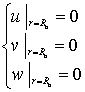

Литература:

1. Кошин, А.А. Технологические проблемы обработки полимерно-композитных материалов / А.А. Кошин // Технологические методы повышения качества продукции в машиностроении (ТМ-2010): сб. тр. Международной научно-технической конференции. Воронеж. – Издательский центр ВГТУ, 2010. – С. 107-111.

2. Кручинин, С.В. Металлополимерные композиционные материалы для ремонтно-восстановительных работ технологического оборудования / С.В. Кручинин, А.В. Липатов, Л.В. Овчаренко, М.М. Феткулин // Ремонт, восстановление, модернизация. – 2002. – № 1. – С. 37–41.

3. Пашнев, В.А. Повышение эффективности шлифования трехслойных металл-композитных систем: дис. … канд. техн. наук / В.А Пашнев. – Челябинск: ЮУрГУ, 2005. – 291 с.