УДК 519.24.001:512,643,5        

ИНФОРМАЦИОННО-ЭНТРОПИЙНЫЙ ПОДХОД К ОЦЕНКЕ КОЛИЧЕСТВА ИНФОРМАЦИИ, КОТОРУЮ ПЕРЕРАБАТЫВАЕТ ЛЁТЧИК В ПРОЦЕССЕ ПИЛОТИРОВАНИЯ

Овчаров Всеволод Ефимович, ОАО«НИИ авиационного оборудования», Россия, 140185, Московская обл., г. Жуковский, ул. Туполева, д.18, главный научный сотрудник, д.т.н. профессор, e-mail orap@list.ru тел. +7.903 550 6290

Курганов Александр Васильевич, ОАО «НИИ авиационного оборудования», Россия, 140185, Московская обл., г. Жуковский, ул. Туполева, д.18, зам. начальника отделения,  к.т.н., доцент, е-mail kurganov@niiao.com, тел.

+7 910 437 35 86

Авакян Александр Анушаванович, ОАО «НИИ авиационного оборудования», Россия, 140185, Московская обл., г. Жуковский, ул. Туполева, д.18,  главный научный сотрудник, д.т.н., профессор, е-mail avakyan@niiao.com, тел.         +7 910 403 74 07.  

Аннотация

Статистика летных происшествий показывает, что существенная доля катастроф происходит по причине человеческого фактора. Летный экипаж, особенно пилоты, за время развития катастрофической ситуации не успевают её парировать (или неправильно парируют), что является причиной возникновения катастроф.

Современные бортовые автоматы полностью автоматизировали функции штурмана, бортинженера и бортрадиста. Реализованная в автоматах авионики воздушных судов гражданской авиации функция автоматического полета автоматизирует этапы горизонтального полета по маршруту и посадку самолета. Летчики выполняют взлет, контролируют полет и парируют нештатные состояния. Однако, наличие человеческого фактора во многих авариях и катастрофах делает актуальным задачу внедрение в автоматы полета процедур парирования критических ситуаций.  

Таким образом, крайне актуальна задача определения количества информации, которую может переработать член летного экипажа или автомат за время развития катастрофической ситуации. Эта задача имеет два аспекта. Первый аспект психологический, т.е. психологические возможности членов экипажа перерабатывать определенное количество информации за определенное время. Относительно этого аспекта в статье приводится только закон Хика, который  определяет зависимость между количеством информации, перерабатываемой оператором при выборе из N однородных  вариантов варианта с заданными характеристиками, и запаздыванием его реакции.  При этом показывается, что информация, перерабатываемая летным экипажем или автоматом, не является набором одинаковых вариантов, а имеет более сложную структуру. Второй аспект проблемы человеческого фактора связан с определением характера и количества информации, которую должен переработать летчик или автомат при штатном пилотировании и парировании критических ситуаций. Именно этому аспекту посвящена настоящая статья.

Показано, что количество информации, перерабатываемой лётчиком при пилотировании, определяется информацией, возникающей при отклонении органов управления и, возникающими при этом, изменениями фазовых координат движения летательного аппарата. В статье рассмотрен один из подходов создания математического аппарата, позволяющего оценить количество этой информации. Подход основан на определении разности между величиной энтропии до начала управления и после того, как управление выполнено. Используя тот факт, что параметры органов управления и фазовые координаты стохастичны и распределены по нормальному закону, а динамическая модель взаимосвязей этих параметров является системой дифференциальных уравнений, было получено выражение для оценки количества информации, вносимой лётчиком в контур управления, а также выражение для временной плотности количества информации. Предложен комплекс работ по реализации полученных результатов.

 

 

Ключевые слова: КОЛИЧЕСТВО ИНФОРМАЦИИ, ЛЕТЧИК, ПИЛОТИРОВАНИЕ, ОРГАНЫ УПРАВЛЕНИЯ, ФАЗОВЫЕ КОРДИНАТЫ, НОРМАЛЬНЫЙ ЗАКОН, ДИНАМИЧЕСКАЯ МОДЕЛЬ, СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, ПЛОТНОСТЬ.

      

Психофизиологические реакция лётчика зависит от ряда факторов, и в том числе, от количества информации, которую лётчик перерабатывает в процессе пилотирования. В психологии известен закон Хика [5], который устанавливает зависимость времени реакции оператора tр на выбор варианта из  «n» одинаковых, равновероятных вариантов. Эмпирическая формула закона Хика имеет следующий вид.

                                                                             (1)

Коэффициенты а и b зависят от профессиональных навыков оператора.         Р. Хартли [5] предложил для оценки количества информации определить логарифм при основании 2 от числа равновероятных вариантов выбора, т. е. количество бит, возникающих при выборе. Как видно из (1), относительно количества информации в битах (по определению Р. Хартли) время реакции имеет линейную зависимость от количества информации.

В практической деятельности лётного экипажа, информация, которую перерабатывают лётчики, представляет собой достаточно сложный набор пилотажной, навигационной информации и информации о состоянии самолетных систем. Вся эта информация представляет многомерную случайную функцию, изменяющуюся в реальном времени. Данная статья посвящена разработке функционалов, с помощью которых можно оценить количества только пилотажной информации перерабатываемой лётчиком в процессе пилотировании летательного аппарата.

Для разработки таких функционалов используется динамическая модель движения самолета. Чтобы не загромождать статью общей динамической системой движения самолета связь параметров управляющих воздействий с фазовыми координатами покажем на примере бокового движения самолета. При этом, управляющим воздействием u(t) будем считать отклонение руля, а выходными величинами модели – фазовые координаты движения летательного аппарата. В статье рассматривается только боковое движение, при котором в результате управляющего воздействия на штурвал u(t) возникает угловое отклонение элеронов dэ(t).

Введем обозначения:

х1 = u – управляющее воздействие, вызывающее отклонение элеронов dэ,

x2 – угловая скорость кренения ωх,

х3 – угол крена g,

х4 – угол курса f,

х5 – линейное боковое уклонение z.

Эти фазовые координаты и угол отклонения элеронов, как известно, в линеаризованной модели [7, Стр. 38] связаны следующими уравнениями:

,

,

(2)
 
,

 ,                                  

 

Кроме того, обозначим

(3)
 
 

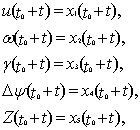
где t0 – момент начала движения, а t – текущее время.

Покажем, что процесс изменения фазовых координат в полете является слу чайным и Гауссовым. Пилот или автомат, управляя полетом самолета, стремятся выполнить полет по некоторой заданной траектории. При полете самолета на его конструкцию, обладающую определенными аэродинамическими характеристиками, влияют множество внутренних и внешних случайных факторов. В текущий момент полета каждый из этих факторов случайным образом либо воздействует на конструкцию, либо не воздействует на неё, т. е. имеет место бинарный закон распределения этих случайных величин.

Реакцией пилота или автомата управляющего полетом, является отклонения управляющего органа (в частности элеронов) на некоторую сумму случайных бинарных величин с целью сохранения полета по заданной траектории. Случайная величина, являющаяся суммой бинарных воздействий, и адекватная ей случайная величина отклонения органов управления, распределены по биноминальному закону. Согласно центральной предельной теореме множество этих случайных отклонений в пределе сходится к нормальному закону распределения. Следовательно, случайный процесс отклонения органов управления относительно некоторого среднего значения, связанного с заданной траекторией, является нормальным (Гауссовым).

При возникновении критических ситуаций (катастрофических, аварийных) случайный процесс изменения фазовых координат остается также нормальным. Меняются параметры нормального процесса, - функция регрессии, остаточная дисперсия. Эти параметры также отражаются в случайной функции плотности распределения параметров и изменяют количество информации перерабатываемой летчиком или автоматом.

Математические выражения перехода бинарного распределения в биноминальный закон и интегральная (центральная) предельная теорема Муавра – Лапласа, доказывающая сходимость биноминального закона распределения к нормальному закону приведены в [6].

Случайный процесс изменения фазовых координат также является нормальным процессом, поскольку он возникает в результате преобразования отклонения органов управления детерминированной динамической системой. Эти предположения подтверждаются анализом случайных процессов изменения фазовых координат фиксируемых бортовыми регистраторами.

Выведем общую формулу количества информации, возникающей в контуре управления при изменении управляющего воздействия (изменении параметра u), т.е. информацию о параметрах пространственного движения самолета. Отображенные на многофункциональных индикаторах параметры движения самолета являются информацией перерабатываемой летчиком.  Для случая, когда известно стохастическое распределение значения параметров до получения информации и после её получения в [2, стр.485] выведена следующая формула количества информации:

 

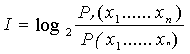                                                                           (4)

 

где:

-     - плотность распределения вероятности параметров до полу                                                                                         чения информации;

-     - плотность распределения вероятности параметров после получения информации

Следовательно, в любой момент времени значения параметров (3) являются случайными числами, а информация о параметрах может рассматриваться как энтропия, т. е. мера неопределенности. Учитывая изложенное и введенные нами обозначения, выражение  (4) может быть преобразовано следующим образом:

     (5)

где:

-     H(t0)-энтропия параметров в момент t0;

-     Hy(t0+t)-энтропия параметров в момент t0+t.

Поскольку распределение полётных параметров является гауссовым, то многомерная функция плотности распределения в момент t0 для «n» параметров будет иметь следующий вид [3, стр. 104]:

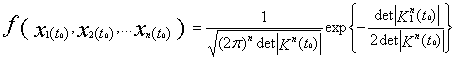                   (6)

Где:

-    

Ковариационная матрица

параметров порядка «n».

 
                                                             (7);

 

 

-    

Ковариационная матрица параметров порядка «n», обрамленная параметрами.

 
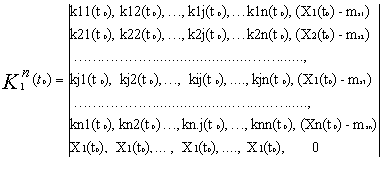                                             (8);

 

-     det(t0)- определитель матрицы (t0) [4];

 

-     det(t0)- определитель матрицы (t0);

 

Ковариационный момент в матрицах (7) и (8) для момента  t0 равен:

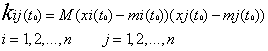
Ковариационный момент в матрицах (7) и (8) для момента  (t0 +t) равен:

 

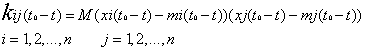
Где M – оператор вычисления математического ожидания.

Для получения выражения количество информации для случая, когда плотность распределения значений параметров подчинено нормальному закону подставим выражение (6) в (5).

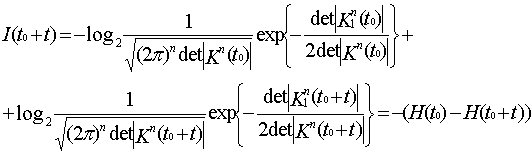     (9)

Учитывая то, что первое слагаемое в выражении (9) относительно текущего времени является постоянной величиной, выражение (9) перепишем следующим образом:

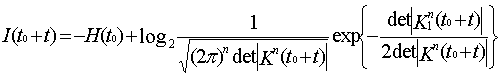              (10)

Поскольку значения параметров динамической системы полета самолета являются случайными, то ковариационные матрицы, входящие в выражение (9) будут случайными функциями. Следовательно, количество информации в зависимости от текущего времени (t) будет также случайной функцией.

Определим усредненное значение количества информации перерабатываемой летчиком за отрезок времени (t-t0), при условии, что динамическая система состоит из «n» параметров. Усредненным значением количества информации, при данном условии будет математическое ожидание от выражения (10) т. е.:

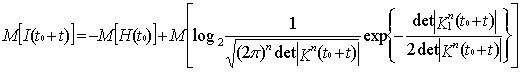 (11)

Поскольку H(t0) не зависит от текущего времени (t), то. Найдем математическое ожидание от второго слагаемого выражения (11).

 

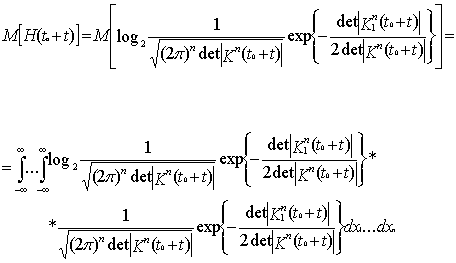                     (12)

В [2, стр.489] показано, что:

                                                                (13)

Таким образом, усредненное количество информации перерабатываемой летчиком за отрезок времени (t-t0), при условии, что динамическая система состоит из «n» параметров равно:

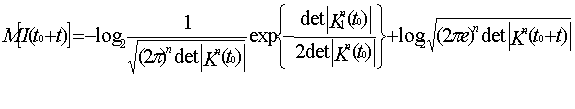      (14)

Усредненное количество информации перерабатываемой летчиком при функционировании динамической системы (2)

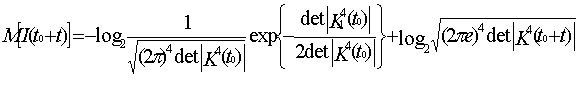       (15)

Кроме усредненной за промежуток времени, в ряде случаев, возникает необходимость определения количества информации за конкретный отрезок времени. Например, представляет интерес расчет количества информации перерабатываемой летчиком при парировании катастрофической ситуации, которая может развивается за секунду. Количество перерабатываемой летчиком информации за любой отрезок времени «Т» можно рассчитать, используя формулу (10), по следующей формуле:

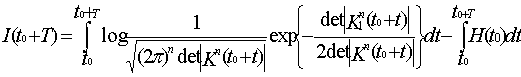                 (16)    

Вывод: полученные в статье результаты могут лечь в основу следующих работ:

1.   Анализ влияния человеческого фактора на развитие катастрофической ситуации при полете летательных аппаратов. Работы должны быть направлены на проведение экспериментов по определению:

-     коэффициентов «а» и «b» формулы (1) для персонального летчика и усредненного летчика,

-     порога нормальной переработки информации летчиком;

-     разработке эффективных тренажерных программ.

2.   Подтверждение гипотез выдвинутых в данной статье о законах распределения параметров полета.

 

 

 

 

 

Литература:

1.   Б.Ф Ломов. «Человек и техника (очерки инженерной психологии)»,            г. Москва,  изд. «Радио», 1966 г.

2.   А.А. Красовский, Г.С.Поспелов. «Основы автоматики и технической кибернетики», г. Москва, г. Ленинград, «Госэнергоиздат», 1962 г.

3.   В.С.Пугачёв. «Теория случайных функций», г. Москва, «Физматгиз»,    1960 г.

4.     Закон Хика, http://usabilist.com.ua/2009/02/zakon-xika/

5.     Количество информации.

Формулы Хартли и Шенона http://marknet.narod.ru/spr/list5.htm.

6.   А.А. Авакян, А.В. Курганов « Физическая модель и закон распределения отказов элементов и систем электроники». Электронный журнал «Труды МАИ», Москва, 2013, выпуск № 71.

7.   В.А.Болдырев, М.С.Козлов «Стабилизация летательных аппаратов и автопилоты», г. Москва, «Оборонгиз», 1961 .

 

 

Авторы:

                               Овчаров В.Е.              Курганов А.В                 Авакян А.А.