Сельское хозяйство/ 2. Механизация сельского хозяйства

д.т.н. Мухин В.А., к.т.н. Дусенов М.К., Сапаргалиев А.С.

Западно-Казахстанский аграрно-технический университет, Казахстан

Определение конструктивно-режимных параметров устройства для очистки картофеля

Во всех известных устройствах для очистки картофеля центробежного типа используются горизонтальные дисковые рабочие органы, с вертикальной осью вращения. Для этой цели в горизонтальных дисках используется крыльчатки различной конфигурации: прямые радиальные и криволинейные с вогнутой и выпуклой формой исполнения [1]. Однако наличие специальных крыльчаток усложняет конструкцию горизонтального диска, снижает ее производительность, не всегда обеспечивает высокое качество очистки картофеля.

Нами была поставлена задача, создать более эффективную конструкцию рабочего органа устройства, в котором для осуществления процесса продвижения картофеля по каналу очистки образованным диском, крыльчаткой и щеткой, наиболее полно использовалось их физические свойства.

Для определения конструктивно-режимных параметров рассмотрим действия сил на картофель при движении по диску (рис. 1) [2]. Горизонтальный диск радиусом R, с криволинейными крыльчатками вращается с частотой ω около вертикальной оси. Криволинейная крыльчатка способствует скольжению продукта, обеспечивает плавное нарастание крутящего момента и сохраняя постоянным угол трения между касательной, и направлением движения.

Движение картофеля массой m происходит вдоль по днищу диска и боковой поверхности криволинейной крыльчатки. При этом сама крыльчатка с днищем установлена под углом α_лд к основанию диска. Угол наклона α_лд днища диска выбран из условия уменьшения угла φ_к защемления картофеля, который по теоретическим данным [3] составляет в среднем φ_к= 12–24⁰. Крыльчатка расположена наклонно против вращения диска. При вращении диска картофель движется вдоль жесткой крыльчатки до периферии. Принимаем, что сопротивление ее движению постоянно от сил трения по диску, крыльчатке и щетки.

В общем случае результирующая сила F_р= m∂²L_л/∂t_л² определяется выражением [4]:

, (1)

где F_цсτ=F_цсcosα_лд – проекция составляющей центробежной силы F_цс на днище крыльчатки (обусловливает движение картофеля вдоль крыльчатки), Н; F_цс= F_цсоsψ – проекция центробежной силы F_ц = mrω² на вертикальную ось, в которой расположена стенка крыльчатки, Н (здесь r – текущее удаление картофеля от оси диска, м; ω – угловая скорость диска, рад/с; ψ – угол между радиальным направлением и направлением крыльчатки, град); G_τ =Gsinα_лд – cоставляющая силы тяжести картофеля, действующая вдоль днища крыльчатки и тормозящее движение картофеля, Н; G_n=Gcosα_лд – составляющая силы тяжести картофеля, действующая по нормали к днищу крыльчатки, Н; F_цсп= F_цсsinα_лд – проекция составляющей центробежной силы F_цс на нормаль к днищу крыльчатки, Н; F_цпс= F_цsinψ – составляющей центробежной силы, действующая по нормали к стенке крыльчатки, Н; F_к = 2mω cosα_лд dL_л/dt_л– сила Кориолиса, направленная перпендикулярно к вектору скорости и действующая в направлении, противоположном направлению вращения диска (L_л и t_л – путь (м) и время (с) движения картофельа вдоль крыльчатки), Н; f₃ – коэффициент трения картофеля по ворсу; φ– угол откоса картофеля, град.

Подставив значения сил в уравнение (1), после элементарных преобразований получим зависимость :

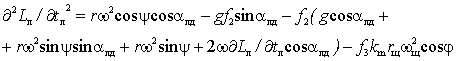, (2)

где k_m – коэффициент учитывающий отношение массы и формы картофеля со щеткой.

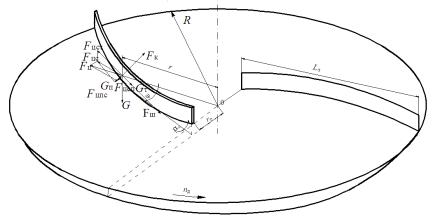
Рисунок 1 – Схема к определению конструктивно-режимных параметров диска

В процессе движения картофеля по крыльчатке радиус изменяется от r_o до R, а угол ψ остается постоянным. Из анализа скольжения картофеля по крыльчатке (рис. 1) вытекает, что r=r_ое^αtgε, L_л²=r_о²+r²–2rr_оcosα, 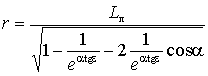, где r_о– начальное удаление картофеля от оси диска и расстояние от оси до крыльчатки.

С учетом этого можно записать уравнение (2) в виде линейного уравнения второго порядка с постоянными коэффициентами. Так как картофель поступают на крыльчатку потоком то их движение вдоль крыльчатки можно принять безотрывным от ее поверхности с начальной скоростью и тогда уравнение (2) будет иметь следующий вид:

, (3)

где λ₁, λ₂,– корни характеристического уравнения; Θ, С₁ и С₂ – постоянные интегрирования.

Относительная скорость v_o движения картофеля вдоль крыльчатки получим путем дифференцирования уравнения (3), после элементарных преобразований получим:

. (4)

Из общей системы уравнений (3–4) можно найти частные решения с учетом формы выполнения диска. Подставляя известные данные в формулу (3-4) получим необходимую длину крыльчатки и скорость движения картофеля в данный момент времени. При известных данных (f₂= 0,6, f₃= 0,3, α_лд= 15⁰, ψ = 30⁰, ω = 1.41 с^-1, k_m = 2, с₁ = 0,8, t = 4,5 с) скорость движения картофеля составит v_ос = 0,66 м/с, необходимую длина крыльчатки составила L_л= 0,371 м, что удовлетворяет конструктивным требованиям очистительных машин [5].

Также можно добавить, что увеличение радиуса диска сопряжено с быстрым увеличением металлоемкости устройства, но зато при малом радиусе диска требуется более точное изготовление устройства в соответствии с выбранной формой крыльчатки и основными параметрами диска.

Литература:

1. Теория, конструкция и расчет сельскохозяйственных машин: учебник для вузов сельскохозяйственного машиностроения / Е. С. Босой [и др.] ; под ред. Е. С. Босого. – 2 изд., перераб. и доп. – М. : Машиностроение, 1977. – 567 с.

2. Дусенов, М. К. Обоснование движения корнеплода по криволинейной поверхности / М.К. Дусенов, Н.Р. Джапаров // Вестник Саратовского госагроуниверситета им. Н. И. Вавилова. – 2007. – № 3. – С. 33–35.

3. Горячкин, В.П. Качение-скольжение по наклонной плоскости / В.П. Горячкин // Собр. соч.: в 3 т. – М.: Колос, 1965. –Т.2.–720 с.

4. Сабликов, М. В. Сельскохозяйственные машины / М. В. Сабликов. – М.: Колос, 1968. –296 с.

5. Дусенов, М. К. Теоретическое определение параметра качества очистки роторно-щеточного очистителя / В. А. Мухин, М.К. Дусенов // Научное обозрение.– 2010.–№6.– С.53-56.