География и геология / 3.Гидрология и водные ресурсы.

К.ф.-м.н. Саноцкая Н.А.

Российский государственный гидрометеорологический университет, Санкт-Петербург, Россия

Предельные распределения максимальных и минимальных расходов воды

В гидрологии широко рассматривается проблема расчетов экстремальных характеристик стока рек. В помощь для разрешения данного вопроса приходит теория порядковых статистик из математики. В данной статье приводятся возможные варианты распределения максимальных и минимальных расходов воды.

Пусть – независимые одинаково распределенные случайные величины с функцией распределения .

Введем следующие обозначения для максимального и минимального значения стока воды , с функциями распределения , .

Задача состоит в том, чтобы найти условия, которые нужно наложить на , чтобы гарантировать существование последовательностей чисел и / или таких, что

Говорят, что последовательность случайных величин или их функций распределения сходится слабо, если существует для всех точек непрерывности предельной функции .

Следовательно, можно пределы представить в виде:

Введем дополнительные обозначения:

– нижняя крайняя точка функции распределения ,

– верхняя крайняя точка функции распределения .

Теорема 1. Предположим, что и существует число такое, что для любого выполняется условие

(*)

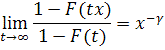
Тогда существует последовательность такая, что

где

Нормирующие константы могут быть выбраны следующим образом:

Теорема 2. Предположим, что и пусть удовлетворяет условию (*). Тогда можно выбрать такие последовательности чисел и , что

где

Центрирующие и нормирующие константы и можно определить следующим образом:

Теорема 3. Если при справедливо соотношение и для функция определена следующим образом . Предположим также, что для любого существует

Тогда существуют последовательности чисел и такие, что

где

Центрирующие и нормирующие константы и можно определить следующим образом:

Теорема 4. Если и существует число такое, что для любого справедливо равенство

(**)

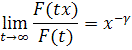
Тогда существует последовательность констант , для которых выполняется равенство

где

Нормирующие константы могут быть выбраны следующим образом:

Теорема 5. Предположим, что и пусть удовлетворяет условию (**). Тогда существуют последовательности чисел и такие, что

где

Центрирующие и нормирующие константы и можно определить следующим образом:

Теорема 6. Пусть при некотором конечном . Предположим, что есть для . Предположим также, что для любого существует

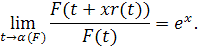
Тогда существуют последовательности чисел и такие, что

где

Центрирующие и нормирующие константы и можно определить следующим образом:

Доказательства теорем приведены в [1].

В гидрологии известно распределение подобного типа как закон распределения крайних членов выборки (распределение Гумбеля) [2].

Для обеспечения проектных работ надежными данными об экстремальных характеристиках стока воды необходимо продолжать внедрять математические методы в гидрологию.

Литература:

1. Галамбош Я. Асимптотическая теория экстремальных порядковых статистик. – М., Наука, 1984. – 304 с.

2. Сикан А.В. Методы статистической обработки гидрометеорологической информации. – СПб.: изд. РГГМУ, 2007. – 279 с.