Lvov A.A., Svetlov M.S., Martynov P.V.

Saratov State Technical University named of Gagarin Y.A., Russia

Evaluation of effectiveness of the non-binary codecs based on the dynamic memory device

At present, especially urgent task is to ensure a high level of the information reliability of digital information and measurement systems, information and control systems due to the constant tightening of requirements. For this purpose, the processing of the signal is carried out while preparing it for the transmission, generally using coding stages in a sequence (concatenated coding) by block codes and continuous error-correcting codes including coded modulation procedure. This allows providing the high rates of noise immunity systems for the transmission of information in channels with high level of noise. In this case, a significant gain is obtained by the use of non-binary codes. Implementing of a reliable synchronous synphased operation of all transmitter-receiver units of systems that use a synchronous serial interface is another task that is no less important in terms of ensuring high reliability of transmission.

Explorations [1] have shown that the use of codecs (encoding and decoding devices) on the basis of dynamic memory devices (DMD) allows successful problem solution of the growth of the information reliability of the digital data transmission systems in general. The peculiarity of these codecs is to represent each bit of the code stream transmitted by the pulse sequences - pulse code series. The pulse code series are formed in the form of tightly linked and fixed by the time intervals (delays) pulses that are multiples of the value Δt and are infinitely small in duration. The main blocks of the codecs generating pulse code series are distribution devices in the form of DMD. Distribution devices based on DMD are universal in the sense that they can be used in systems with code alphabets of any basis (valence).

This work is devoted to optimizing the choice of scheme realization of the algorithms of coding and decoding of non-binary codes using the n-position distribution devices based on DMD. Let q be the number of symbols in the working code alphabet (q≥3), and p - the number of bits required writing one q-ary symbol:  (rounded up to the nearest whole number).

The greatest interest among the developed by the authors variants of embodiments of codecs based on DMD [1] for q-ary codes is the analysis of the following variants:

- Implementation of codecs with two outputs and one DMD, a similar implementation of it for the binary code (variant 1);

- Implementation of codecs with two outputs and p DMD (variant 2);

- Implementation of codecs with 2p outputs and one DMD (variant 3).

 

Evaluating the effectiveness of the algorithms is carried out on the basis of the criterion proposed by the authors in [2]. In accordance with this criterion, coefficients of effectiveness  are calculated for each variant of the decoding algorithm:

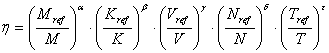,                                  (1)

where M - size of memory required for the implementation of the algorithm; K - the number of auxiliary variables in the structure of the algorithm; V - the number of branches in the structure of the algorithm; N - the number of actions performed in the course of the algorithm (algorithm complexity); T - algorithm execution time, Mref, Kref, Vref, Nref, Tref - reference (the minimum possible) values of the criterion parameters; α, β, γ, δ, ε - integer (for the convenience of calculations) positive weight coefficient that take into account the «weight» (the importance) of the each criterion parameter.

Conducting the analysis of the algorithms let’s consider the general case where the "weight" parameter in equation (1) is equal to unit:

.                                               (2)

The input sequence of characters of the m length can be represented by a polynomial form relative to fictitious variable x:

,                                        (3)

where a1, a2, ..., am - elements of the input sequence (the characters of the using alphabet).

To enable the implementation of polynomials of the form (3) on the element base aimed at work with binary codes, q-ary coefficients can be represented in binary form:

. (4)

For the convenience of the implementation of the q-ary codes polynomial (4) can be represented in the form of system of p polynomials:

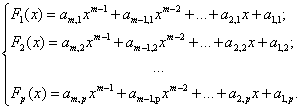                                          (5)

2p pulse code series described by polynomials of code series of binary codes are formed with the implementation of coding and decoding algorithms by the variant 1:

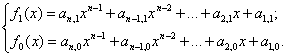                           (6)

The number of pulse code series transmitted to the channel increases in p times in comparison with variants of using binary codes.

It is necessary to use the methods of work with parallel data streams to implement the algorithm according to the variant 2: encoding and decoding devices include two outputs but codecs contain p DMD operate in parallel to each other.

In the implementing of variant 3 codecs contain one DMD with 2p outputs and form 2p pulse code series for each of the polynomials of the system (5):

 

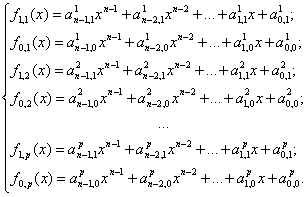                       (7)

 

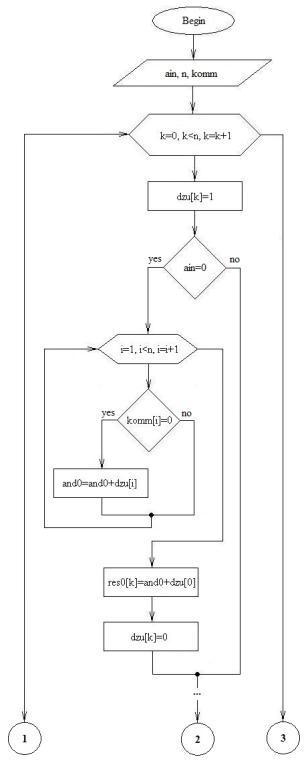
Fig. 1. Block-scheme of encoding device with p outputs on base of DMD for q-ary code

 

 

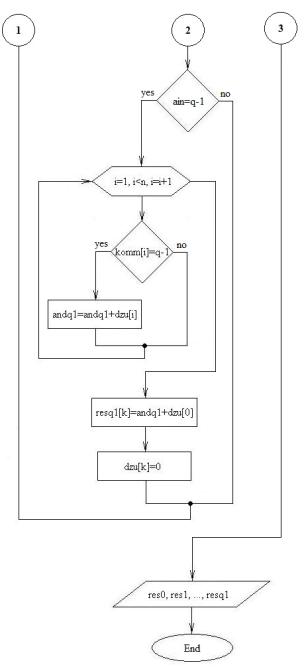
Fig. 2. Block-scheme of decoding device with p outputs on base of DMD for q-ary code

 

Block-schemes of encoding and decoding devices for general case are presented on Fig. 1 and 2. The quantity of branches of case operators in the body of generic algorithm is defined by quantity of symbols in the code alphabet (q). Definitions: ain - input signal, n – quantity of cells of DMD, komm – array which defines the commutation of DMD outputs, dzu – array with meanings of bytes in cells of DMD, and0, and1, …, andq1 – meanings on 0, 1, …, (q-1) output of DMD, res0, res1, …, resq1 – arrays of code series for “0”, “1”, … “q-1”, aout - output signal of decoding device.

Let’s consider the evaluation of the given methods of implementation of DMD for q-ary codes using the proposed criterion.

Size of memory is determined by the number of variables and dimensions of arrays involved in the implementation of the corresponding algorithm. From the analysis of the generic block-schemes of encoding and decoding devices (Fig. 1 and 2) it can be calculated as follows:

• Variant 1 - M1=p(4n+6+3n+4)=p(7n+10). For solving the evaluation task we can accept M1≈7np;

• Variant 2 - M2=7np;

• Variant 3 - M3=7n.

 

The analysis of the obtained expressions shows that the minimum size of memory is required to implement the algorithm by the variant 3. We take the given value of size of memory for reference value and introduce the notation: Mref =M3=7n. Thus, the values of the efficiency coefficients of the algorithms in terms of size of memory take the form:

The number of auxiliary variables required to implement each algorithm is defined as follows:

·           variant 1 – K1=p(2+n)≈np;

·           variant 2 – K2=p(2+n)≈np;

·           variant 3 – K3=Kref=n+5≈n.

 

The values of efficiency coefficients of the algorithms in the number of auxiliary variables take the form:

The number of branches from the analysis of the body of each algorithm can be calculated as follows:

·        variant 1 – V1=10np=Vref;

·        variant 2 – V2=10np=Vref;

·        variant 3 – V3=n2(1+q)+8n+2nq+1≈qn2+2nq+8n≈qn2.

 

Values of the effectiveness of the algorithms on the number of branches:

The number of operations performed in the algorithm:

·        variant 1 – N1=p(7n2+7n+17n+9)≈p(7n2+24n)≈7pn2;

·        variant 2 – N2=p(7n2+7n+17n+9)≈p(7n2+24n)≈7pn2;

·        variant 3 – N3=7n2+28n+nq≈7n2=Nref.

The values of efficiency coefficients of the algorithms on the complexity take the form of:

From the analysis of the structure and complexity of each algorithm it follows that the minimum time necessary for the performance of the algorithm for variant 2 with the use of parallelizing the operations of coding and decoding of each of the bits of the binary representation of q-ary code. We introduce the notation: T2 = Tref = t. Time of execution of the other algorithms can be defined as follows:

• Variant 1 - T1 = k1*t, where k1>0 - integer coefficient;

• Variant 2 - T2 = Tref =t;

• Variant 3 - T3 = k2*t, where k2>0 - integer coefficient. Due to the fact that the complexity of the algorithm is lower than complexity of the algorithm by variant 1, the correct relation is: k2 < k1.

 

The values of efficiency coefficients of the algorithms according to the execution time take the form :

The values of each criterion of efficiency of the each algorithm according to the formula (2):

The value of each of the coefficients belongs to the interval . If the value is closer to unity, the efficiency of the algorithm is higher. That’s why if you take the weight coefficient in the formulae equal to unity, then, based on selected criteria, the most effective is the algorithm in the variant 3 -implementation of q-ary codes based on one DMD with p outputs.

 

Literature

1. Martynov P.V. Increasing of noise immunity in communication data systems with radio channels / P.V. Martynov, M.S. Svetlov // Bulletin of the Saratov State Technical University ¹ 1 (64), issue 2, 2012. - P. 328-331.

2. Martynov P.V. The development of criteria of the effectiveness of the algorithms of digital information processing / N.A. Lvova, P.V. Martynov // Collection of scientific papers of the II International Conference "Problems of control, transmission and processing of information" (ATM-2011), Vol. 2, Section 2, 2012. - P. 72-74.