Математика/ 1. Диференціальні і інтегральні рівняння

К.ф.-м.н.  Казмерчук А.І.

Прикарпатський національний університет імені В.Стефаника

Гладкість компонент розв’язку системи квазілінійних диференціальних рівнянь першого порядку

При вирішенні питання розв’язності задач для систем квазілінійних рівнянь першого порядку, враховуючи наявність у розв’язках розривів навіть при досить гладких даних задачі, важливим виявляється аналіз умов, які забезпечують гладкість окремих компонент розв’язків. При наявності розривів доцільним є вивчення систем, коефіцієнти яких на розривних розв’язках залишаються гладкими. Цим обумовлено вибір потокових функцій в системі квазілінійних рівнянь першого порядку.

Нехай система квазілінійних рівнянь першого порядку   має вигляд         

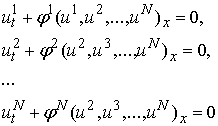(1)

де , , .

Шукаємо ентропійний розв’язок  задачі Коші для системи (1)  з початковою умовою

(2) де , . Надалі вважаємо, що система (1) гіперболічна та сильно нелінійна ([1]).

Означення Обмежена вимірна вектор-функція  називається узагальненим розв’язком задачі (1), (2), якщо система (1) розуміється у сенсі розподілів, виконується ентропійна умова ([2]) на розривах, та початкова умова (2) приймається у слабкому сенсі.

Теорема 1 Нехай  і . Тоді узагальнений розв’язок задачі (1), (2) існує, а за умови єдиний. Крім цього .

Цей результат випливає з методів роботи [2].

Отже, при розв’язок в загальному випадку не є гладкий.

Теорема 2 Нехай  . Тоді в смузі існує гладкий розв’язок задачі Коші для підсистеми (1) з .

За виконання умов, що гарантують принцип максимуму, з теореми 2 випливає існування узагальненого розв’язку задачі (1), (2), у якому всі компоненти окрім першої є гладкими функціями.

Зауважимо, що отримані результати можуть бути застосовані в газовій динаміці, механіці суцільних середовищ при моделюванні закону руху ідеального азу або рідини ([3]).

Література:

1. Lax P.D. Hyperbolic system of conservation laws.-Comm. Pure Appl.Math.-1957.-V.10.-p.537-566.

2. Казмерчук А.І. До обґрунтування наближених методів розв’язання квазілінійних законів збереження з негладкими даними задачі. - Вісник національного університету “Львівська політехніка”, Прикладна математика.-2000.-№411.-с.147-151

3. Рождественский Б. Л., Яненко Н. Н. Системы квазилинейніх уравнений и их приложения в газовой динамике.- М., Наука.- 1978