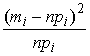КРИТЕРИИ СОГЛАСИЯ В АВТОСЕРВИСЕ

Критерии согласия в автосервисе

Ладин Р.А., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Установим согласованность «теоретического» нормального закона распределения со статистическим распределением люфта (случайной величины) в рулевом управлении. Для этого воспользуемся методами теории проверки статических гипотез. А именно, критериями согласия, с помощью которых определяют качество согласования гипотетического теоретического закона распределения случайной величины с экспериментальными данными (из расхождений между теоретическими вероятностями и наблюденными частотами ). В качестве меры расхождения между «теоретическим» и статистическим распределениями будем рассматривать случайную величину

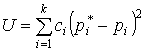Отклонения относятся к разным разрядам, поэтому по значимости они, в общем случае, не равноправны: одно и то же по абсолютной величине отклонение может быть малозначительным, если сама вероятность велика, и очень заметным, если она мала. Поэтому веса обычно принимаются пропорциональными вероятностям разрядов , то есть предполагается, что 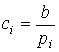. Возникает вопрос, как выбрать коэффициент пропорциональности . Известно, если число опытов , а 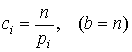, то закон распределения практически не зависит от функции распределения и от числа опытов , а зависит только от числа разрядов . А именно, закон распределения приближается к распределению с плотностью распределения

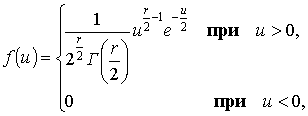
где гамма-функция 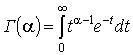. Как видим, распределение зависит от числа степеней свободы . Оно равно числу разрядов за исключением числа независимых условий (связей), наложенных на частоты :

, , ,

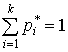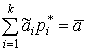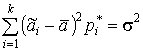так что .

При этом

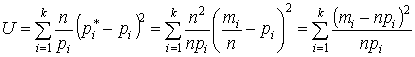Если величина действительно распределена по нормальному закону, то 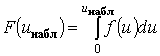характеризует вероятность того, что за счет чисто случайных причин мера расхождения теоретического нормального и статистического распределений не превосходит величину , то есть

Воспользуемся приведенной методикой для оценки нормальности распределения люфта (в градусах) в рулевом управлении. Статистический ряд, полученный по экспериментальным данным, приводится в таблице 1.

Таблица 1.

Интервал

4,28-4,38

4,38-4,48

4,48-4,58

4,58-4,68

4,68-4,78

4,78-4,88

4,88-4,98

Частота

Относительная частота

0,04

0,09

0,17

0,30

0,27

0,11

0,02

По приведенным выше формулам вычислим эмпирическое среднее 4,638, выборочное среднее квадратическое отклонение =0,133180,133, теоретические вероятности попадания значений в -й разряд (табл.2).

Таблица 2.

Интервал	Эмпирическая частота	Вероятность	Теоретическая частота
4,28-4,38	4	0,0233	2,33	2,7889	1,197
4,38-4,48	9	0,0930	9,30	0,009	0,0097
4,48-4,58	17	0,2123	21,23	17,8929	0,8428
4,58-4,68	30	0,2909	29,09	0,8281	0,0285
4,68-4,78	27	0,2324	23,24	14.1376	0,6083
4,78-4,88	11	0,1093	10,93	0,0289	0,0026
4,88-4,98	2	0,0301	3,01	1,0201	0,3389
		∑0,9913			=∑3,0278

Для выбранного уровня значимости при числе степеней свободы по таблице - распределения находим критическое значение . Так как , т.е. , то нет оснований отвергнуть гипотезу о нормальном распределении значений люфта.

Некоторые другие примеры использования критериев согласия рассматриваются в [1,2].

Литература

1. Данилов А.М.,Гарькина И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. - Пенза: ПГУАС, 2011. -296 с.

2. Данилов А.М., Гарькина И.А. Теория вероятностей и математическая статистика с инженерными приложениями. - Пенза: ПГУАС, 2010 г. - 228 с.