Некоторые Приложения Корреляционного анализа

Паршина К.С., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Условное математическое ожидание величины Y можно рассматривать как функцию от x (). Функция называется регрессией Y по X; уравнение - уравнением регрессии Y по X; линия, определяемая этим уравнением в плоскости XOY, называется линией регрессии Y по X (для дискретных величин “линия” будет состоять из изолированных точек плоскости). Аналогично определяются регрессия , уравнение регрессии и линия регрессии величины X по Y. Наиболее простым случаем является тот, когда обе функции регрессии

,

являются линейными и обе линии регрессии будут прямыми линиями. Эти прямые называются прямыми регрессии.

Уравнения прямых регрессии, получаемые по эмпирическим данным, имеют вид:

; ,

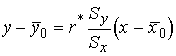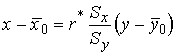где 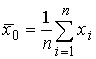, 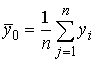- эмпирические (выборочные) средние; 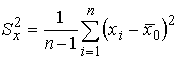, 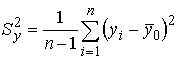- эмпирические (выборочные) дисперсии; 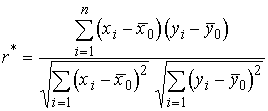- эмпирический (выборочный) коэффициент корреляции.

Теоретический коэффициент корреляции случайных величин X, Y определяется как отношение корреляционного момента

K_{x, y} = M [(X-M[X]) (Y - M[Y]]

к произведению средних квадратических отклонений этих величин:

.

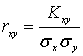Коэффициент корреляции по абсолютной величине не превышает 1 (½r_xy ½ £ 1), причём, чем ближе r_xy к 1, тем больше корреляционная зависимость между X и Y приближается к линейной, а при ½ r_xy ½ = 1; случайные величины связаны линейной функциональной зависимостью. Если r_xy = 0, то X и Y не связаны линейной корреляционной зависимостью, но могут быть связаны нелинейной корреляционной или даже функциональной зависимостью.

Воспользуемся приведенным выше для определения зависимости коэффициента теплопроводности l , Вт / (м² ×) жаростойкого бетона с заполнителем из магнезита от средней температуры нагрева по данным эксперимента:

	100	300	600	700	900	1100
l	5,90	5,35	4,78	4,20	3,60	3,00
m	2	3	3	4	4	2

С учетом оценок математических ожиданий ; для системы центрированных случайных величин и корреляционная таблица будет иметь вид:

							nt
	-1,41	-0,81	-0,21	0,37	0,94	1,49
-538,9						2	2
-338,9					3		3
-38,9				3			3
61,1			4				4
261,1		4					4
461,1	2						2
nl	2	4	4	3	3	2	18

Получим следующие оценки:

,; , ;;

(корреляционная зависимость между X и Y близка к линейной).

Эмпирические прямые регрессии имеют вид:

; .

Для оценки точности выборочного значения r^* используем функцию:

.

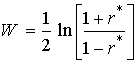Распределение случайной величины W можно аппроксимировать нормальным распределением со средним значением и дисперсией вида

, .

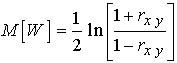На основе этих соотношений легко построить доверительные интервалы для r_xy по выборочной оценке r^*. Из-за выборочной изменчивости оценок корреляции обычно приходится проверять, свидетельствует ли ненулевое значение выборочного коэффициента корреляции о существовании статистически значимой корреляции между изучаемыми величинами. Сделать это можно, проверив гипотезу r_xy = 0, причём отклонение гипотезы будет говорить о значимости корреляции. При r_xy = 0 выборочное распределение W будет нормальным со средним M [ W ] = 0 и дисперсией . Поэтому область принятия гипотезы о нулевой корреляции будет иметь вид:

,

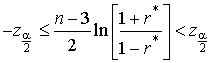где z - стандартная, нормально распределённая случайная величина. Если значение окажется вне этого интервала, то это будет признаком наличия статистической корреляции с уровнем значимости a. Для рассматриваемого случая 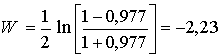; при этом .

Гипотеза r_xy должна быть отвергнута с уровнем значимости 5 % , поскольку не попадает в область принятия гипотезы, ограниченную величинами . Следовательно, есть основания считать, что между коэффициентом теплопроводности и средней t ^o нагрева существует значимая связь.

Для качественного анализа при исследовании зависимостей могут использоваться и более простые методы, в частности, методы ранговой корреляции [1].

Литература

1. Данилов А.М., Гарькина И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. - Пенза: ПГУАС, 2011. -296 с.