К.т.н. Круглова А.Н., к.п.н. Ячинова С.Н.

Пензенский государственный университет архитектуры и строительства, Россия

Определение фрактальной размерности изображений

К настоящему времени известны различные способы количественного определения соответствия изображений в серии испытаний. Многие из них сопоставляют растровому образу (изображению) некоторый скалярный параметр (интересующие исследователя характерные элементы изображения определяют способ вычисления). Вполне удовлетворительные результаты можно получить с использованием такого скалярного параметра, как фрактальная размерность. Строгое определение фрактальной размерности восходит к работам Г. Минковского и Ф. Хаусдорфа. Размерность Хаусдорфа может быть сравнительно просто вычислена только для самоподобных множеств – фракталов; в общем случае определение размерности Хаусдорфа весьма громоздко [1].

При определении фрактальной размерности изображения предпочтительным является отказ от использования глобального порога яркости; видоизменённый алгоритм анализа должен фиксировать локальные различия яркостного поля. Таким алгоритмом, в частности, является алгоритм двоичной декомпозиции изображения. Суть указанного алгоритма состоит в последовательном анализе изображения на различных масштабных уровнях. При переходе к каждому последующему уровню размер анализируемой области уменьшается в два раза. В алгоритме в качестве исследуемой области берется исходное изображение. Определяются минимальное и максимальное значения яркости в этой области. Если разность между максимальным и минимальным значением не превышает заданного порогового значения (порога разложения), то область рассматривается как лист двоичного дерева (листу сопоставляется среднее арифметическое минимального и максимального значений яркости – т.н. конечное значение яркости). В противном случае исследуемую область делится на две подобласти (в зависимости от размеров – вертикальной или горизонтальной прямой) и алгоритм рекурсивно применяется (со второго шага) для каждой подобласти. Так алгоритм представляется в виде древовидной структуры данных. Листы представляют участки изображения, в пределах которых яркость сохраняет приблизительно постоянное значение. Для данного порога разложения глубина двоичного дерева и зависимость числа листов от уровня определяются пространственным распределением яркости. Поэтому набор двоичных декомпозиций, выполненных для различных порогов разложения, исчерпывающим образом характеризует пространственное распределение яркости.

Информативность полученного описания определяется использованием большого числа доступных зависимостей и скалярных параметров: характеристики общей однородности (глубина двоичного дерева и ее зависимость от порога разложения); зависимость числа листов (логарифм) от уровня дерева (устанавливает характерный масштаб, на котором возникает пространственная неоднородность); построенные для каждого уровня дерева и для каждого порога разложения вариационные ряды; характеристика, связывающая пространственный масштаб и доминирующее значение яркости (зависимость среднего по уровню конечного значения от глубины дерева).

Исходной дискретной функции дерево двоичной декомпозиции сопоставляет две другие дискретные функции: функцию , совпадающую с конечным значением листа, покрывающего элемент в строке r и столбце c; а также функцию , значение которой связано с глубиной листа, покрывающего элемент в строке r и столбце c. Графические образы этих функций (матриц конечных значений и уровней) являются визуальными представлениями двоичной декомпозиции.

Конечной целью древовидной декомпозиции является получение некоторого количественного критерия (выражается одним числом). Так для каждого масштабного уровня деревьев двоичной декомпозиции можно использовать их заселённости:

,

где N_l – число листов двоичного дерева на уровне l. Отметим, что заселённость уровня можно трактовать как произведение фрактальной размерности на номер масштабного уровня. Действительно, с учётом при имеем , поэтому при больших l (важно, что увеличение номера уровня l соответствует уменьшению масштаба):

.

Откуда:

;

аналогия с определением размерности по Минковскому очевидна.

Таким образом, частное от деления заселённости на номер уровня имеет смысл фрактальной размерности.

Литература:

1. Данилов А.М., Смирнов В.А., Королёв Е.В., Круглова А.Н. Фрактальный анализ микроструктуры наномодифицированного композита // Нанотехнологии в строительстве №5 2011 г.
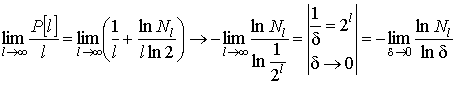