И.А. Долгарев и А.И. Долгарев

ОПРЕДЕЛЯЕМОСТЬ ЕВКЛИДОВОЙ ПОВЕРХНОСТИ.

ОБНОВЛЕННАЯ ОСНОВНАЯ ТЕОРЕМА ТЕОРИИ ПОВЕРХНОСТЕЙ

(обзор теории поверхностей)

В связи с новыми исследованиями по теории евклидовых поверхностей, затронуты следующие вопросы. Явное задание поверхности. Выражение коэффициентов второй квадратичной формы поверхности через коэффициенты первой квадратичной формы в случае явного задания поверхности. Определяемость регулярной евклидовой поверхности. Обновленная основная теорема теории поверхностей. Получение поверхности по коэффициентам первой квадратичной формы как обычная задача. Задание поверхности дифференциальными уравнениями.

1. Основные понятия

1.1. Регулярная евклидова поверхность

Рассматриваются регулярные класса поверхности 3-мерного евклидова пространства , заданные в произвольной параметризации

= = ,, (1)

векторы , неколлинеарны. Точки регулярной поверхности называются обыкновенными; точки, в которых происходит нарушение регулярности, называются особыми. Рассматриваются регулярные поверхности в окрестности обыкновенной точки. Векторы , , являются касательными к поверхности в точке . Касательная плоскость имеет своим векторным пространством оболочку .

На поверхности (1) рассматриваются линия , линия и произвольные линии , которые задаются вектором

= = . (2)

1. ТЕОРЕМА. Регулярная поверхность (1) в каждой своей обыкновенной точке обладает касательной плоскостью .

Направление линии на поверхности определяется вектором касательной = , задается отношением или .

Прямая называется нормалью поверхности (1) в точке , вектор нормали поверхности есть .

1.2. Метрическая квадратичная форма поверхности

Обозначая

, , , (3)

имеем первую основную квадратичную форму или метрическую форму регулярной поверхности (1) :

(4)

с коэффициентами (3). Детерминант метрической формы поверхности равен

, , . (5)

На основе метрической формы поверхности вычисляются: длина линий на поверхности, величины углов между линиями на поверхности, площади областей поверхности.

1.3. Нормальная кривизна линий на поверхности.

Квадратичная форма кривизны поверхности

Пусть естественный параметр линий на поверхности (1), т.е. = , тогда кривизна линий на поверхности (1) определяется из равенства

,

где единичный вектор главной нормали кривой . Обозначим

(6)

единичный вектор нормали поверхности (1) и пусть угол между векторами и . Величина

называется нормальной кривизной линий (2) на поверхности (1) .

Пусть

; ; , (7)

см. (5). Имеем:

, (8)

или, с использованием (8),

= = . (9)

Квадратичная форма

= (10)

называется второй основной квадратичной формой или формой кривизны регулярной поверхности (1) . Согласно (9):

2. ТЕОРЕМА. Нормальная кривизна линий на регулярной евклидовой поверхности (1) равна отношению формы кривизны поверхности и метрической формы.

1.4. Индикатриса кривизны.

Классификация обыкновенных точек евклидовой поверхности

Каждая из линий

, (11)

в касательной плоскости поверхности (1) , называется индикатрисой кривизны (индикатрисой Дюпена) поверхности в ее обыкновенной точке .

Коэффициенты (7) формы кривизны (10) вычислены в точке . Индикатриса (11) является центральной линией второго порядка; это либо эллипс, либо две сопряженные гиперболы, либо пара параллельных несовпадающих прямых. Вид индикатрисы кривизны определяет ее детерминант

.

Обыкновенные точки поверхности (1) различаются по детерминанту индикатрисы (11).

(а) . Детерминант индикатрисы положителен, индикатриса является эллипсом. Точка называется эллиптической. Касательная плоскость в точке имеет с поверхностью (1) только одну общую точку – точку .

(б) . Индикатриса есть пара гипербол. Точка называется гиперболической. Касательная плоскость пересекается с поверхностью (1) по двум прямым – общим асимптотам гипербол.

(в) . Индикатриса есть две параллельные прямые. Точка называется параболической. Касательная плоскость пересекает поверхность (1) по прямой.

(г) . Индикатриса превращается в точку. называется точкой уплощения. В этой точке по всем направлениям . Если (1) – плоскость, то всякая ее точка есть точка уплощения.

1.5. Полная и средняя кривизна поверхности

В каждой обыкновенной точке поверхности (1) на касательной плоскости индикатриса кривизны определяет два главных сопряженных направления, они взаимно перпендикулярны. Кривизны нормальных сечений поверхности (1) в главных

направлениях называются главными и обозначаются . Произведение

называется полной или гауссовой кривизной поверхности в точке , полусумма

называется средней кривизной поверхности в точке .

=, . (12)

1.6. Замечательные поверхности

(а) Плоскость = . Коэффициенты (3) метрической формы (4) постоянны и хоть один отличен от нуля. По (7), форма кривизны (10) нулевая. По (12),

, .

Полная и средняя кривизны плоскости постоянны и равны нулю.

Каждая точка плоскости есть точка уплощения, п. 1.4. Существуют и другие поверхности, имеющие нулевую полную кривизну, например, цилиндр = .

(б) Сфера = . Коэффициенты метрической формы сферы и детерминант формы равны: = , = 0, = ; = . Коэффициенты формы кривизны сферы равны: ; ; . По (12) вычисляем:

= , = .

Полная и средняя кривизны сферы постоянны и положительны.

(в) Псевдосфера = . Коэффициенты метрической формы псевдосферы: =, = 0, . = ; коэффициенты формы кривизны поверхности: = ; = 0; . Находим:

= , .

Полная кривизна псевдосферы отрицательна и постоянна. За это свойство рассматриваемая поверхность названа псевдосферой.

1.7. Явное задание регулярной поверхности

Параметризация (1) регулярной евклидовой поверхности произвольна. Ввиду регулярности поверхности, от параметризации (1) можно перейти к параметризации

= ; (13)

в окрестности обыкновенной точки, см.[1, 72 – 73; 2, 209 – 211]. В этом случае имеем задание поверхности явной функцией

. (14)

3. ТЕОРЕМА. Всякая регулярная евклидова поверхность в окрестности всякой своей обыкновенной точки задается явной функцией (14), или равнозначно, векторной функцией (13).

Находим по (3) и соответственно (7):

, , ; =; (15)

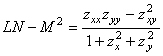, , ; . (16)

Поэтому, согласно (12),

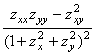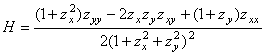= , . (17)

Величина

(18)

называется 2-детерминантом поверхности (14) или функции .

4. ТЕОРЕМА. Знак полной кривизны поверхности (14) совпадает со знаком 2-детерминанта поверхности.

1.8. Экстремумы функции двух переменных

Необходимым условием существования экстремума функции (14) во внутренней точке области задания поверхности является

, . (19)

Достаточный признак существования экстремума функции (16) в точке связан с 2-детерминантом поверхности , [3, с. 273] и с видом обыкновенной точки , [4].

5. ТЕОРЕМА. В точке поверхности (14) при условии (19) существует экстремум, если эта точка эллиптическая; и отсутствует экстремум, если эта точка гиперболическая.

1.9. Сопровождающий репер поверхности.

Соприкасающийся параболоид поверхности

В каждой обыкновенной точке поверхности (1) определены неколлинеарные векторы касательных и единичный вектор (6). Тем самым, в каждой обыкновенной точке поверхности задан репер

,

это сопровождающий репер поверхности (1). Во всякой обыкновенной точке поверхности (14) существует соприкасающийся параболоид

, (20)

[5, с. 26; 6, с. 345;]. В случае соприкасающийся параболоид описывается функцией

,

см. [5, с. 26]. Отмечается, [5, с. 84], что в произвольной обыкновенной точке поверхности уравнение соприкасающегося параболоида (20) не совпадает с уравнением рассматриваемого параболоида.

1.10. Об основной теореме теории поверхностей и внутренней геометрии поверхности

В трудах Гаусса, Петерсона, Кодацци, Бонне и других в XIX веке установлены основные положения теории поверхностей. Это прежде всего теорема Гаусса о том, что полная кривизна поверхности выражается через коэффициенты метрической формы поверхности и их производные. Теорема Гаусса позволила выделить внутреннюю геометрию поверхности. К ней относятся свойства поверхностей, основанные на метрической (первой основной) квадратичной форме поверхности [2, с. 334]. Доказана основная теорема теории поверхностей – теорема Петерсона-Бонне о том, что коэффициенты метрической формы поверхности и формы кривизны поверхности определяют поверхность с точностью до положения в пространстве. Однако недавно получено, [7], что коэффициенты формы кривизны регулярной евклидовой поверхности выражаются через коэффициенты ее метрической формы. Этот факт изменяет отношение к основным квадратичным формам поверхности. Доказательство теоремы Петерсона-Бонне очень сложное, в учебниках по теории поверхностей теорема только упоминается. Значительных упрощений в определяемости евклидовой поверхности можно добиться, рассматривая галилеевы квадратичные формы евклидовой поверхности, [8]. Определяется евклидова поверхность и своей первой квадратичной формой. Указанные вопросы освещены ниже.

2. Галилеевы свойства евклидовой поверхности.

2.1. Геометрия многообразия

Существует арифметическая модель аффинной геометрии. Точками аффинного пространства являются тройки действительных чисел, векторами аффинного пространства являются его параллельные переносы, записываемые в виде троек действительных чисел, они составляют линейное пространство над . Точки и векторы связаны аксиомами Г.Вейля. На многообразии выполняется аффинная геометрия. Если и векторы, , то определены операции над векторами

, .

Паре точек и соответствует вектор

.

Прямые аффинного пространства описываются векторными функциями

,

это прямая , проходящая через точку в направлении вектора . Плоскости аффинного пространства описываются векторными функциями

,

это плоскость , проходящая через точку и имеющая неколлинеарные векторы и .

Возможно, что в линейном пространстве аффинного пространства введено евклидово скалярное произведение векторов и :

и евклидов модуль вектора равен

.

Возможно, что в линейном пространстве введено галилеево скалярное произведение векторов и , см. [9, с. 33]:

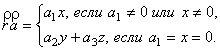
Галилеев модуль вектора равен:

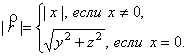(21)

компонента вектора называется временной, компоненты называются пространственными.

В результате введения евклидова скалярного произведения векторов в , аффинное пространство превращается в евклидово пространство , линейное пространство становится евклидовым векторным пространством . В результате введения галилеева скалярного произведения векторов в линейном пространстве , аффинное пространство становится пространством-временем Галилея , линейное пространство становится галилеевым векторным пространством . Точки пространства-времени Галилея называются еще событиями. Событие состоит в том, что точка рассматривается в момент времени . Множество = всех событий составляет мир.

Событиям и , соответствует вектор = . Галилеева норма вектора , или галилеево расстояние между точками и вычисляется, согласно (21), следующим образом

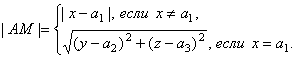
Объекты аффинного пространства , в том числе плоскости и поверхности, обладают как евклидовыми, так и галилеевыми свойствами. Евклидовы свойства объектов выявляются в результате введения в линейном пространстве аффинного пространства евклидова скалярного произведения векторов; галилеевы свойства объектов выявляются в результате введения в галилеева скалярного произведения векторов. Тем самым, мы имеем единую геометрию многообразия , ее составными частями является аффинная геометрия, евклидова геометрия, галилеева геометрия и всякая геометрия со скалярным произведением векторов. Галилеева дифференциальная геометрия изложена в [9, с. 46 – 101].

2.2. Выделенная параметризация евклидовой регулярной поверхности

Пусть (1) есть регулярная евклидова поверхность класса . Для функции существует функция , поверхность (1) задается в параметризации

= , . (22)

В таком виде задается регулярная галилеева поверхность в естественной параметризации, [9, с. 71 – 100]. Параметризация (22) евклидовой поверхности называется выделенной. Частным видом выделенной параметризации (22) является параметризация (13) евклидовой поверхности, задающая поверхность явной функцией (14).

Производные первого порядка функции (22) есть

, .

Векторы неколлинеарны. Каждая точка поверхности (22) является обыкновенной. Если поверхность (22) галилеева регулярная, то вектор является галилеевым единич-

ным, а вектор является евклидовым и .

2.3. Галилеевы квадратичные формы евклидовой поверхности

Определены галилеевы квадратичные формы евклидовой поверхности в [4, 8], они согласованы с галилеевым квадратом вектора (21) и с квадратичными формами галлеевых поверхностей, [9, с. 73 и с. 77 – 78].

ОПРЕДЕЛЕНИЕ. Первой основной галилеевой квадратичной формой регулярной евклидовой поверхности (22) в выделенной параметризации называется

,

коэффициент называется галилеевой метрической функцией поверхности и равен

= . (23)

Вектор

(24)

называется единичным вектором галилеевой нормали евклидовой поверхности (22).

ОПРЕДЕЛЕНИЕ. Второй основной галилеевой квадратичной формой регулярной евклидовой поверхности (22) в выделенной параметризации называется

,

, , . (25)

Полная галилеева кривизна евклидовой поверхности (22) равна

, (26)

аналог формулы Гаусса в геометрии Галилея, согласно [9, с. 94], таков

. (27)

2.4. Об основной теореме галилеевой теории евклидовых поверхностей

По формулам коэффициентов (23), (26) галилеевых квадратичных форм евклидовой поверхности (24) в выделенной параметризации и вектору (24) галилеевой нормали поверхности (22) записывается система дифференциальных уравнений с частными производными:

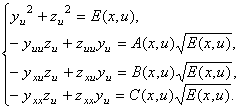(28)

По аналогии с основной (неуточненной) теоремой галилеевой теории евклидовых поверхностей, п. 1.10, справедлива

6. ТЕОРЕМА. [8] Если на некоторой односвязной области евклидовой плоскости заданы класса функции

, , , (29)

– коэффициенты первой и второй галилеевых квадратичных форм поверхности (22), то компоненты евклидовой поверхности = (22) являются решением системы дифференциальных уравнений с частными производными (28). Начальные условия вида

, ,

, , , (30)

определяют единственную поверхность, проходящую через точку и имеющую векторы касательных , . Коэффициенты квадратичных форм найденной поверхности совпадают с заданными.

Cхема доказательства теоремы 6 такова. Вводим обозначения по виду первого уравнения системы (28)

, , (31)

функцию предстоит найти. Дифференцируем функции (31) по параметру , результат подставляем во второе уравнение системы (28), получаем . Далее дифференцируем функции (31) по параметру , и по третьему уравнению системы (28), находим . Решением уравнения с полным дифференциалом

является функция , введенная в (31). Интегрируем (31) по параметру :

, . (32)

Дифференцируя дважды функции по параметру и воспользовавшись четвертым уравнением системы (31), отыскиваем функции . В результате становятся известными функции . Поверхность = имеет квадратичные формы с коэффициентами (29). Начальные условия (30), задающие точку поверхности и касательные векторы в этой точке, определяют единственную поверхность.

Пусть теперь евклидова регулярная поверхность задана функцией (13) = . Имеем: , , ; по (25): , , . Так как , , то , и второе и третье уравнения в системе (28) не нужны.

7. ТЕОРЕМА. [8, теорема 2] Если заданы функции

, , (33)

то функция (14) , описывающая явно регулярную евклидову поверхность, является решением системы дифференциальных уравнений с частными производными

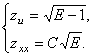(34)

Начальные условия вида (30) выделяют единственную поверхность (14) с коэффициентами (33) квадратичных форм.

Система уравнений (28) превращается в (34). Ее решение значительно проще, чем решение системы (28). Находим . Функция отыскивается по второму уравнению системы (34). Это теорема об определяемости регулярной евклидовой поверхности одним коэффициентом галилеевой метрической формы и одним коэффициентом галилеевой формы кривизны.

2.5. Евклидовы поверхности с постоянными коэффициентами

галилеевых квадратичных форм

8. ТЕОРЕМА. [10, теорема 3]. Пусть коэффициенты галилеевых квадратичных форм регулярной евклидовой поверхности постоянны. Если полная галилеева кривизна евклидовой поверхности равна нулю, то поверхность цилиндрическая:

= , .

Если полная галилеева кривизна евклидовой поверхности отлична от нуля, , то поверхность является прямым геликоидом.

9. ТЕОРЕМА. [10, теорема 1] Если на односвязной области евклидовой плоскости заданы постоянные величины , , то на этой области определяется прямой геликоид

= ,

коэффициенты первой и второй галилеевых квадратичных форм которого равны заданным величинам. Начальные условия , определяют единственный геликоид, содержащий точку и имеющий касательную плоскость, натянутую на векторы .

10. ТЕОРЕМА. [10, теорема 4] Единственной евклидовой поверхностью постоянной ненулевой полной галилеевой кривизны является прямой геликоид; его полная галилеева кривизна отрицательна, коэффициенты галилеевых квадратичных форм постоянны. #

В этом состоит уникальность прямого геликоида.

11. ТЕОРЕМА. [10, теорема 2] Поверхность с коэффициентами , и постоянной галилеевой кривизной не существует.

Если коэффициенты (3) метрической формы евклидовой поверхности (1) в произвольной параметризации постоянны, то по (3) векторы постоянны. Тогда коэффициенты формы кривизны нулевые, см. (10). Выполняется

12. ТЕОРЕМА. Евклидова поверхность, коэффициенты форм метрической и кривизны которой постоянны, является плоскостью.

3. Определяемость евклидовой поверхности

коэффициентами первой евклидовой квадратичной формы

3.1. Выражение коэффициентов второй квадратичной формы поверхности

через коэффициенты ее первой квадратичной формы. Определяемость поверхности

Регулярная евклидова поверхность в окрестности всякой своей обыкновенной точки задается явной функцией (14), и векторной функцией (13). В [7] для явно заданной поверхности получены выражения коэффициентов формы кривизны через коэффициенты метрической формы. Приведем эти результаты в виде теоремы

13. ТЕОРЕМА. [7, теорема 1] Коэффициенты (7) формы кривизны евклидовой регулярной поверхности (13) в явном задании выражаются через коэффициенты метрической формы следующими формулами

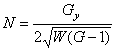, , . (35)

# По (15) имеем . Дифференцируем формулы из (15):

, , , .

Откуда находим

= , , , .

Теперь получаем первую и третью формулы в (35). Перемножаем значения производных , получаем с использованием второй формулы из (15):

,

а отсюда имеем вторую формулу в (35). # Заметим, что в формуле для в [7, c. 56] допущена опечатка: вместо напечатано .

Согласно п. 1.10, регулярная евклидова поверхность однозначно, с точностью до положения в пространстве, определяется коэффициентами первой и второй квадратичных форм. В окрестности всякой обыкновенной точки регулярная поверхность задается явной функцией. Следствием теоремы 13 является следующая

14. ОБНОВЛЕННАЯ ОСНОВНАЯ ТЕОРЕМА ТЕОРИИ ПОВЕРХНОСТЕЙ. [7, теорема 5] Коэффициенты формы кривизны евклидовой регулярной поверхности являются функциями коэффициентов метрической формы и их производных первого порядка независимо от параметризации поверхности.

Теорема установлена двумя независимыми способами: как следствие теоремы 13, т.е. как теорема 14, и как теорема 15 ниже.

Принято выделять внутреннюю геометрию поверхности. Согласно [1, c. 225]: «Те геометрические свойства поверхности, которые можно установить, исходя из задания только первой квадратичной формы, образуют так называемую внутреннюю геометрию поверхности.» Но по теореме 13, свойства поверхности, которые можно установить, исходя из задания первой и второй квадратичных форм поверхности, можно установить и только исходя из коэффициентов первой квадратичной формы поверхности. Значит, внутренняя геометрия поверхности имеет более конкретное содержание, которое связано с изгибанием поверхности, [7].

3.2. Функция , как решение системы дифференциальных уравнений

В [12] рассматривается система линейных уравнений

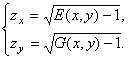(36)

15. ТЕОРЕМА. [12, теорема 2] Если на односвязной области евклидовой плоскости заданы действительные дифференцируемые функции двух аргументов

, (37)

удовлетворяющие условиям

,

то на этой области определяется поверхность (14) с точностью до положения в пространстве, для которой функции (37) являются коэффициентами формы кривизны. Начальные условия

,

выделяют единственную поверхность, проходящую через точку и имеющую в этой точке касательную плоскость

, , .

По функциям (37) составлена система обыкновенных дифференциальных уравнений (36), решением которой является функция (14) , задающая поверхность, коэффициенты метрической функции которой есть (37). В [12] по функциям , найдены параболоиды и по функциям ,

, найден прямой геликоид , .

3.3. Добавочные возможности метрической формы евклидовой поверхности

После основной теоремы 14 евклидовой теории поверхностей выполняется

16. ТЕОРЕМА. [12, теорема 8] Все свойства поверхности, выраженные через коэффициенты первой и второй квадратичных форм поверхности, выражаются только через коэффициенты первой квадратичной формы и их производные.

В связи с этим справедливы следующие утверждения.

17. ТЕОРЕМА. [7, теорема 1] Для явно заданной поверхности полная кривизна выражается через коэффициенты ее метрической формы и производные первого порядка этих коэффициентов и имеет вид

. (38)

18. ТЕОРЕМА. [12, теорема 2] Средняя кривизна регулярной евклидовой поверхности выражается через коэффициенты метрической формы поверхности и производные первого порядка этих коэффициентов:

.

19. ТЕОРЕМА. [12, теоремы 3,4] Нормальная кривизна линий на евклидовой регулярной поверхности выражается через коэффициенты метрической формы и производные первого порядка этих коэффициентов и имеет вид

.

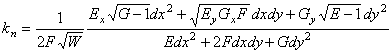В направлении на евклидовой регулярной поверхности нормальная кривизна линий на поверхности вычисляется по формуле

.

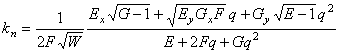Формулы теорем 17 – 19 получены в результате подстановки значений коэффициентов (35) формы кривизны в соответствующие формулы классической теории поверхностей. На основе формулы (38) полной кривизны поверхности выполняется

20. ТЕОРЕМА. [12, теорема 7] Обыкновенная точка евклидовой регулярной поверхности является эллиптической, если в этой точке величины

и

отличны от нуля и имеют одинаковые знаки; является гиперболической, если указанные величины отличны от нуля и имеют противоположные знаки; и точка является параболической или точкой уплощения, если

.

3.4. Еще одна квадратичная форма поверхности

Вопросы определяемости поверхности

В связи с явным заданием (14) евклидовой регулярной поверхности возникает еще одна квадратичная форма поверхности, [13]:

ее коэффициенты есть

. (39)

21. ТЕОРЕМА. [13, теорема 3] Коэффициенты (39) квадратичной формы поверхности (14) однозначно, с точностью до положения определяют явно заданную регулярную евклидову поверхность. #

22. ТЕОРЕМА. [13, теорема 4] Коэффициенты (39) квадратичной формы определяют коэффициенты первой основной квадратичной формы регулярной евклидовой поверхности

, , ; .

Полная кривизна поверхности равна

.

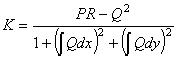23. ТЕОРЕМА. [13, теорема 5] Евклидова регулярная поверхность (14) определяется с точностью до положения, если заданы коэффициенты ее второй квадратичной формы , , и детерминант первой квадратичной формы . Заданные функции подчиняются условиям

, , .

Начальные условия как в теореме 15 выделяют единственную поверхность, проходящую через точку и имеющую касательную плоскость

в заданной точке , .

Функции , , определяются равенствами (35).

24. ТЕОРЕМА. [13, теорема 10] Коэффициенты формы кривизны поверхности не определяют поверхность; кроме коэффициентов формы кривизны должен быть задан детерминант метрической формы поверхности.

4. Дифференциальные уравнения и векторнрые поля поверхности

4.1. Системы дифференциальных уравнений поверхностей

Решениями многих дифференциальных уравнений с частными производными и их систем являются компоненты функций, задающих регулярные евклидовы поверхности.

25. ТЕОРЕМА. [13, теорема 1] Однородное уравнение второго порядка с частными производными

, (40)

коэффициенты которого подчиняются условиям

, (42)

имеет своим решением 2-параметрическое семейство функций

, постоянные.

Начальные условия вида

.

выделяет единственную поверхность, проходящую через точку и имеющую касательную плоскость в заданной точке .

В условиях теоремы 25 при вместо (42) имеем

, .

в этом случае выполняется

26. СЛЕДСТВИЕ. [13, следствие 2] Решением дифференциального уравнения

при условиях теоремы 25 является семейство линейных функций .

27. ТЕОРЕМА. (на основе [13]) Решение системы уравнений с частными производными

, ,

где коэффициент формы кривизны поверхности детерминант метрической формы поверхности, совпадает с решением уравнения с полным дифференциалом и совпадает с решением уравнения (40).

4.2. Ортогональность векторных полей поверхностей

Задавая регулярную евклидову поверхность явной функцией (14) имеем плоское скалярное поле , [14], градиент поля (14)

нормален линиям уровня поля (14). Векторные линии поля (14) составляют решение уравнения

,

а векторные линии поля составляют решение уравнения

.

28. ТЕОРЕМА. [14, теорема 6] Скалярное поле ортогональное данному полю на области характеризуется полем направлений с касательными векторами линий уровня

.

Линии уровня являются решением дифференциального уравнения

, ,

функция находится как решение дифференциального уравнения

.

Справедливо следующее

29. СВОЙСТВО. [14, свойство 8] Поле и поле , каждое в отдельности, однозначно определяют поверхность.

30. СВОЙСТВО. [14, свойство 9] Градиент и дивергенция связаны соотношением

.

Литература

1. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. - М.: Наука, 1979. - 560с.
2. Рашевский П.К. Курс дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.

3. Фихтенгольц Г.М. Основы математического анализа, т.I. М.: ГИТТЛ, 1956. – 464с.

4. Долгарев И.А. Галилеевы квадратичные формы евклидовой поверхности.// Метрическая геометрия поверхностей и многогранников. Междунар. Конф., посв. 100-летию со дня рождения Н.В. Ефимова. Москва, 18 – 21 авг. 2010. Сборник тезисов. М.: МАКС Пресс, 2010. - С. 24 – 25.

5. Розендорн Э.Р. Теория поверхностей. – М. ФИЗМАТЛИТ, 2006. – 304 с.
6. Выгодский М.Я. Дифференциальная геометрия. – М. – Л.: Гостехиздат, 1949. – 512 с.
7. Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверхностей.// Materiali IX mezinarodni vedecko-praktika conference «Dni vediy – 2013» - Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and Skience”. s.r.o. – 2013. С. 55 – 60.
8. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.
9. Долгарев И.А., Долгарев А.И. Галилеевы идеи в курсе евклидовой дифференциальной геометрии.// Вестник Красноярского педуниверситета им. В.П. Астафьева, 2013 № 1(23), Красноярск, 2013, С. 232 – 235.
10. Долгарев И.А., Долгарев А.И. Прямой геликоид среди евклидовых поверхностей.// Materiali IX mezinarodni vedecko-hraktika conference «Dni vediy – 2013» - Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and Skience”. s.r.o. – 2013. С. 7 – 14.
11. Долгарев А.И. Добавочные возможности первой квадратичной формы евклидовой поверхности. // Materialy IX Miedzynarodowej naukowi-praktycznej konferencji “Dinamika naukowych badan – 2013” Volume 12. Matematyka. Fizyka. Nowoczesne informacyjne technologie. Chemia I chemiczne technologie: Przemysl. Nauka i studia – 2013, C. 20 – 26.
12. Долгарев А.И. Система линейных уравнений первого порядка в частных производных. Задание евклидовой поверхности коэффициентами ее первой квадратичной формы. // Materiali IX mezinarodni vedecko-praktika conference «Dni vediy – 2013» - Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and Skience”. s.r.o. – 2013. С. 32 – 40.
13. Долгарев А.И. Уравнение второго порядка с частными производными, сведение к уравнениям первого порядка. Еще одна квадратичная форма поверхности. // Materialy IX Miedzynarodowej naukowi-praktycznej konferencji “Dinamika naukowych badan – 2013” Volume 12. Matematyka. Fizyka. Nowoczesne informacyjne technologie. Chemia I chemiczne technologie: Przemysl. Nauka i studia – 2013, C. 3 – 10.
14. Долгарев И.А., Долгарев А.И. Вектоные поля евклидовых регулярных поверхностей. // Materialy IХ mezinarodni vedecko-praktika conference «Vedecky pokrok na prelomu tysyachalety – 2013» Dil 34. Matematika. – Praha: Publishing House “Education and Science” s.r.o. 2013, p. 47 – 54.