Математика/5. Математическое моделирование
Челабчи В.В., Челабчи В.Н.
Одесский национальный морской университет, Украина
Управляемая идентификация моделей динамических систем
Для повышения эффективности и минимизации затрат энергии и ресурсов в
действующих и проектируемых установках и системах требуются надежные методы и
средства прогнозирования их функционирования в различных условиях. Как правило,
натурный эксперимент и физическое моделирование требует значительных материальных
и финансовых затрат, а часто практически невозможны. Вычислительный эксперимент
на основе математического моделирования позволяет провести исследование быстрее
и дешевле. Особенно важно обеспечить достаточную достоверность
получаемых в эксперименте результатов при минимизации затрат.
При исследовании переходных процессов в детерминированных динамических системах с сосредоточенными параметрами используются математические модели в виде систем обыкновенных дифференциальных уравнений (ОДУ) получаемых на основе феноменологического подхода или путем идентификации элементов действующих систем на базе экспериментальных данных. Чаще всего проблема идентификации объектов сводится к решению задачи параметрической идентификации, когда вид уравнения математической модели заранее выбран.
Как правило, экспериментальные данные (воздействие на
объект Xe и реакция объекта Ye ) зашумлены. Для получения ясной
картины исследуемого процесса требуется подавить зашумленность. В этом случае
уместно использовать сглаживание зашумленных экспериментальных данных с
аппроксимацией на скользящих отрезках. На каждом выделенном
отрезке времени используется локальная в пределах каждого отрезка независимая
переменная t .
Схема расположения узлов (моментов времени) приводится на рис. 1.
Зависимости Xе(t) и Yе(t) в пределах каждого отрезка аппроксимируются полиномами невысокой степени. Аппроксимация функций на отрезках осуществляется методом наименьших квадратов и вычисляются значения аппроксимирующих функций Xa, Ya и их производных для каждого значения аргумента отрезка.
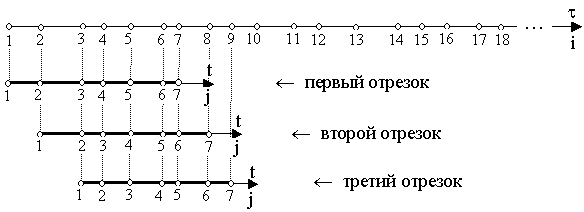

Рис. 1. Схема разбиения области определения функции на отрезки при аппроксимации и идентификации методом скользящих отрезков
где t –
глобальное время, t – локальное время
При сглаживании значения Xa и Ya для каждого значения t обрабатываются многократно. Сглаженные значения Ys, Ys’, Ys” рассчитываются по формулам (1).
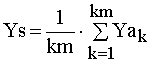 ,
, 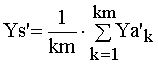 ,
, 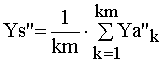 , (1)
, (1)
где km – количество обработок значений аргумента t.
Для
повышения качества сглаживания проводится многократное сглаживание [1], когда в
качестве исходных данных используются результаты предварительного сглаживания.
Для решения задачи идентификации [2] используется простой и надежный метод наименьших квадратов, включающий следующие этапы.
a) Вся область изменения величин Xs(τ) и Ys(τ) разбивается на отрезки времени Dt, перекрывающие друг друга. Используется метод скользящих отрезков (Рис.1). На каждом выделенном отрезке используется локальная в пределах каждого отрезка независимая переменная t.
b) Проводится аппроксимация зависимостей Xs=f(t) и Ys=f(t) на отрезках оси времени гладкими неразрывными функциями. На выбор вида аппроксимирующих функций существенных ограничений нет. Авторы использует полиноминальную аппроксимацию полиномом порядка kpol.
c)
Значения
функций и производных подставляются в идентифицируемое уравнение и определяется
сумма квадратов невязок левой и правой частей уравнения (минимизируемый функционал
δ) для всех рассматриваемых моментов времени.
d)
Значения
коэффициентов идентифицируемого уравнения определяются путем минимизации функционал
δ. Можно использовать методы спуска, но при полиноминальной аппроксимации
полученную систему линейных алгебраических уравнений удобно решать одним из
прямых методов.
Качество результатов идентификации математической модели объекта оценивается сравнением значений Ys и восстановленных значений Yp полученных путем решения идентифицированного уравнения управляемым проекционным методом.
При анализе результатов используется оценки (2) или (3).
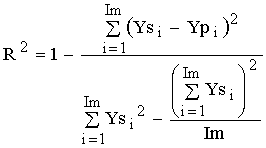 , (2)
, (2)
где Ys, Yp - соответственно, сглаженное и восстановленное значение ункций,
Іm - количество
значений моментов времени.
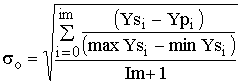 . (3)
. (3)
Проекционное решение обыкновенных дифференциальных уравнений базируется на вариационном подходе [3]. Основная идея метода заключается в том, что на отрезках z оси независимой переменной τ (Рис.2) в качестве решения Y принимается функция определенного типа, но с неизвестными пока параметрами (коэффициентами). В пределах каждого отрезка Dt используется локальная независимая переменная t.
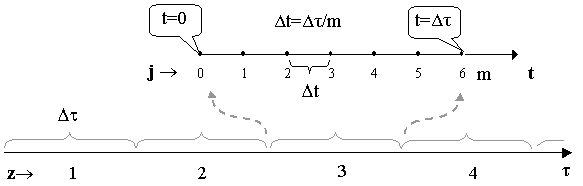
Таким образом, создается последовательность
отрезке z, каждый из которых включает достаточное
количество внутренних узловых точек j.
Рис. 2 Схема индексации узлов сетки при проекционном решении
Для аппроксимации проекционного решения авторы используют полиномы степени kp.
Выражения для функции и ее производных подставляются в решаемое уравнение. Записывается выражение для функционала δ, который представляет собой сумму квадратов невязок (разностей значений правой и левой частей уравнения) для ряда значений независимой переменной. Коэффициенты аппроксимирующей функции находятся путем минимизации функционала δ. Полученная система линейных алгебраических уравнений решается прямым методом.
При настройке проекционного решения на каждом отрезке Dt осуществляется управляемый подбор значений kp, m с целью обеспечения желаемого уровня погрешности решения [3].
Общий алгоритм управляемой идентификации
обыкновенных дифференциальных уравнений представлен на блок-схеме рис. 3.
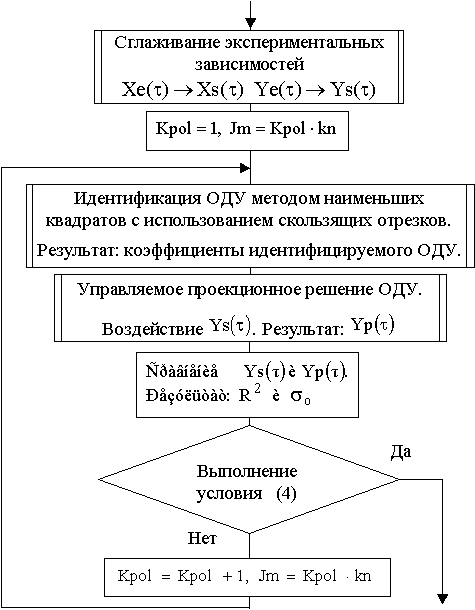
Рис. 3 Схема алгоритма управляемой идентификации ОДУ
При управляемой идентификации ОДУ предварительно проводится сглаживание экспериментальных зависимостей.
Сам процесс идентификации выполняется итерационно при вариации порядка аппроксимирующего полинома kpol и количества моментов времени входящих в отрезок Jm.
Окончание итерационного процесса идентификации осуществляется при выполнении условия (4).
![]() . (4)
. (4)
Оценка эффективности предложенного алгоритма проводилась при решении многих тестовых задач. Имитация экспериментальных зависимостей осуществлялась путем наложения на точные аналитические решения полосы шума Dsh различного вида и уровня (Рис.4).
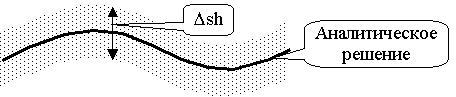
Рис. 4 Схема имитации экспериментальных зависимостей
Результаты исследований позволяют рекомендовать:
![]() ,
, ![]() ,
, ![]() .
.
Литература:
1. Меркт Р.В., Челабчи В.В., Челабчи В.Н. Особенности сглаживания экспериментальных зависимостей методом скользящих отрезков / Сб. научных трудов по материалам международной научно-практической конференции «Современные направления теоретических и прикладных исследований ‘2011». Том 8. Физика и математика. – Одесса: Черноморье, 2011. с.18-22.
2. Челабчи В.В., Челабчи В.Н. К вопросу идентификации динамических объектов / Вторая Международная научно-практическая конференция «Спецпроект: анализ научных исследований»: Сб. научных работ. Том 3. – Днепропетровск: НАЦ ”ЕРА”, 2005. –с. 52-55.
3. Челабчи В.В. Оперативное управление проекционно-сеточным методом при решении обыкновенных дифференциальных уравнений / Сборник научных трудов SWorld. Материалы международной научно-практической конференции «Современные проблемы и пути их решения в науке, транспорте, производстве и образовании ‘2012». – Выпуск 4. Том 3. Физика и математика. – Одесса: КУПРИЕНКО, 2012 - с.49-53.