Математика/ 5. Математическое моделирование

к.ф.-м.н. Искакова А.С.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

О вероятностно-статистическом исследовании одной модели квадратичного прогнозирования

В работе [1] были представлены алгоритмы линейного и квадратичного прогнозирования. При рассмотрении примера применения дискретного линейного прогнозирования к фондовой биржевой системе с количеством показателей k=24. По ежедневным статистическим данным за 2010-2011 гг. для всех показателей k=24 была формирована реализация выборки объема n=720, представляющая относительные ошибки фактических данных к прогностическим значениям.

Исходя из природы изучаемой модели прогноза, о распределении относительной ошибки фактического значения к прогностическому можно лишь утверждать, что она принадлежит некоторому семейству распределений. Например, это распределение может быть нормальным, лог-нормальным, показательным и т.д. То есть необходимо определить аппроксимирующий вид распределения вероятности оправдываемости прогноза. Следовательно, стоит задача в построении статистической оценки вероятности.

1. Статистическое оценивание неизвестных параметров

При построении статистических оценок часто основным требованием является моделирование оценок с отсутствием систематических погрешностей в наблюдаемых данных. Иными словами, приоритетными статистическими оценками являются несмещенные. Существуют множество способов построения несмещенных оценок, но метод максимального правдоподобия, обладая простотой построения и хорошими асимптотическими свойствами, является широко использованным.

С использованием метода максимального правдоподобия, были получены оценки вероятностей оправдываемости представленной модели.

Оценка максимального правдоподобия совместной плотности нормального распределения имеет вид

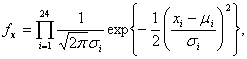
где μ₁,…, μ₂₄, σ ₁,…, σ₂₄ - оцениваемые параметры. Неизвестные определены по методу максимального правдоподобия.

Для совместной плотности бета распределения оценка максимального правдоподобия имеет вид

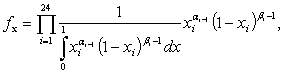
где α₁,…, α₂₄, β₁,…, β₂₄ оцениваемые параметры.

Также оценка максимального правдоподобия совместной плотности гамма распределения имеет вид

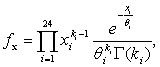
где k₁,…,k₂₄, θ₁,… , θ₂₄ оцениваемые параметры.

Если предположить, что вероятность оправдываемости прогноза имеет логнормальное распределение, то оценка максимального правдоподобия совместной плотности имеет вид

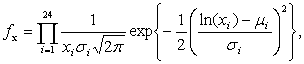(1)

где μ₁,…, μ₂₄, σ ₁,…, σ₂₄ - оцениваемые параметры.

Оценка максимального правдоподобия совместной плотности экспоненциального или показательного распределения имеет вид

где λ₁,..., λ₂₄ оцениваемые параметры.

2. Статистическая проверка гипотез

Были рассмотрены значения статистик хи-квадрат для нормального распределения. В этом случае максимальное значение статистики Пирсона есть

полагая, что количество частичных интервалов выборки есть 10, то, соответственно, степень свободы принимает значение 7. Следовательно, уровень значимости α=10^-6.

При десяти частичных интервалов выборки максимальное значение статистики Пирсона при бета-распределения есть

В соответствии с методами статистического анализа получаем, что уровень значимости α=0.

И соответственно, максимальное значение статистики Пирсона при гамма- распределении есть

Здесь, аналогично, уровень значимости α=0.

При логнормальном распределении максимальным значением статистики Пирсона является

Как видно, уровень значимости α=0,06.

В случае показательного распределения максимальное значение статистики Пирсона есть

Так как показательное распределение имеет только один параметр, то степень свободы принимает значение 8. Следовательно, уровень значимости α=0.

Таким образом, из полученных результатов видно, что для данного примера оценка максимального правдоподобия вероятности оправдываемости прогноза определяется по формуле (1). Анализ проведенных вычислений позволяет сформулировать следующие основные результаты. Для представленного примера, в соответствии с оценкой максимального правдоподобия совместной плотности экспоненциального распределения (1), оценка математического ожидания относительной ошибки принимает значение 0,1573, оценка дисперсии - 0,0668, оценка медианы - 0,1091, оценка моды - 0.

Это говорит о том, что вероятность оправдываемости представленной модели прогноза очень высокая. Полученная формула (1) оценки плотности вероятности можно считать критерием оправдываемости представленного прогнозирования.

Список литературы

1. Өтелбаев М., Сейтқұлов Е., Каюпов Т., Төлеуов Б., Искакова А., Жүсiпова Д. Корреляциялық геокосмостық тәуелдiлiктi математикалық модельдеу және болжаудың әдiстерi. // Вестник ЕНУ имени Л.Н. Гумилева. Серия естественно-технических наук. – 2012. - № 4 (89). – С. 6-14.