Математика/5. Математическое моделирование

Аспирант С. В. Гаевой, аспирант Ф. А. Х. Аль-Хадша,

д.т.н. В. С. Лукьянов

Волгоградский государственный технический университет, Волгоград

Эвристики распределения заявок в Грид-системах (Grid)

Система Грид (Grid) состоит из узлов, именуемых кластерами. Каждый кластер построен из вычислительных машин. В Грид-систему поступают задания, которые надо рассчитать. Весь расчет ведется в пределах одного кластера [1].

В [2][3] нами уже поднимался вопрос моделирования Грид-систем с точки зрения оптимального распределения заданий по кластерам и был создан программный продукт [4].

Кластера, как правило, собираются из машин равной производительности [5]. Введем понятие эталонной машины [1] с единичной производительностью. Сложность задания будем измерять временем исполнения на одной эталонной машине.

Каждое задание может исполняться параллельно на нескольких машинах. Это количество, называемое шириной [6], прописано в момент создания [7]. Распараллеливание будем вести в соответствии с законом Амдаля.

Каждый кластер имеет неограниченную очередь заданий на исполнение. Ближе к началу расположены задания с более высоким приоритетом (при совпадении — созданные раньше).

Стратегии распределения заданий являются эвристиками, то есть позволяют определить кластер путем эмпирических оценок [1][6]. Всем узлам присваивается стоимость исполнения задания. Выбирается узел с наименьшей оценкой, а при совпадении — с меньшим номером.

1) Rotate.

, где - номер оцениваемого кластера (от нуля), - количество кластеров для выбора, - кластер, который получил последнее задание (стартовое значение равно ).

2) FreeExec. С корректируем оценку из [6]

, где - количество машин кластера, - количество свободных машин кластера. Используется при быстром выполнении заданий в отсутствие очереди.

3) QueueWidth. Оценка из [6]

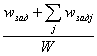, где - количество машин, необходимое заданию, для которого определяется кластер, - количество узлов, необходимое j-му заданию в очереди кластера, - количество машин кластера.

4) QueueLen. Модификация оценки QueueWidth

, где - длина очереди кластера, - количество машин кластера.

5) QueueDif. Оценка от [6]

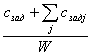, где - сложность задания, для которого выбирается исполнитель, - сложность j - го задания в очереди кластера, - количество узлов кластера.

6) QueueProd. Оценка (наша модификация оценки №5)

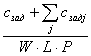, где - сложность задания, для которого выбирается исполнитель, - сложность j - го задания в очереди кластера, - количество узлов кластера, - поправочный коэффициент (будем считать равным единице для всех кластеров), - производительность узла.

7) MaxProd

, где - производительность узла, - количество узлов кластера.

Для оценки стратегий воспользуемся методом имитационного моделирования, методом дискретных событий. В отличие от [2][3][4], мы построим детерминированную имитационную модель [8][9].

Для примера возьмем систему, состоящую из следующих кластеров: №0 (8 машин производительности 2,0), №1 (12 по 1,2), №2 (16 по 1,0), №3 (20 по 0,5). Будем варьировать параметры заданий: приоритет от 0 до 2 с шагом 1, сложность от 0,7 до 1,3 с шагом 0,1, долю последовательного кода от 0,0 до 0,2 с шагом 0,05. Требуемое число узлов (ширину) будем варьировать так: 1, 2, 4, 8. Итого получаем различных комбинаций заданий. Пусть каждая комбинация встречается в системе 100 раз. Значит, необходимо пропустить через систему 31,5 тыс. заданий. Сделаем так, чтобы все задания поступали в начальный момент времени. Исследования будем проводить в двух вариантах: с распараллеливанием выполнения заданий (Parallel) и без (Sequential).

Для получения результатов стохастического моделирования используем модификацию [4]. Обозначим стохастический вариант звездочкой (*). Параметры заданий в этом случае будут случайными равномерно распределенными величинами в выше указанных диапазонах, причем сложность и доля последовательного кода будут распределены непрерывно, а ширина и приоритет — дискретно.

Нас интересуют два показателя: время выполнения всего пакета заданий (рис. 1) и среднее время выполнения одного задания (рис. 2). Как мы видим, использование распараллеливания не является полезной функцией при большом числе заданий. Также можно видеть, что стохастический и детерминированный варианты дают близкие и во многих случаях одинаковые результаты. Самой удачной на данном примере является стратегия QueueProd. Она учитывает и параметры очереди, и параметры кластеров.

Таким образом, были предложены эвристики распределения заданий между несколькими исполнителями, а для оценки качества эвристик были построены имитационные модели. В дальнейшем планируется провести детерминированное и стохастическое моделирование для логов работы реальных вычислительных систем, предоставляемых [7].

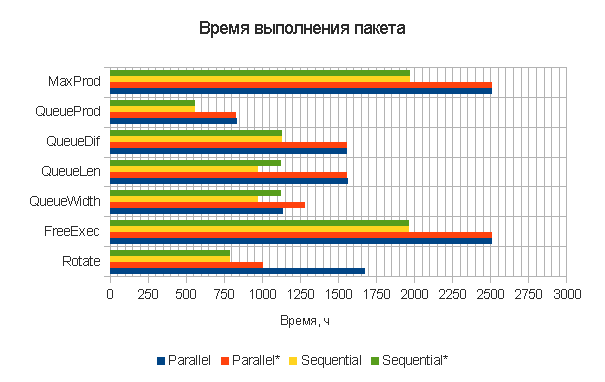
Рисунок 1 — Время выполнения пакета

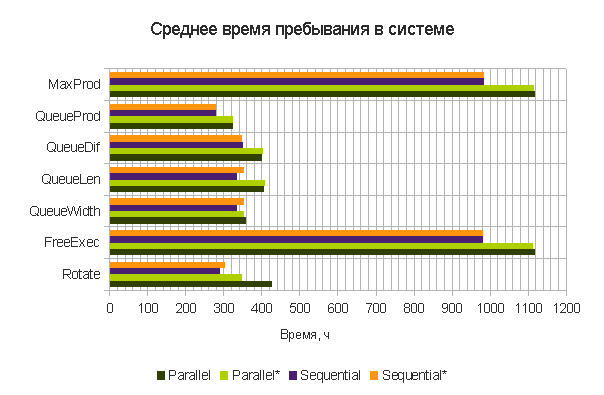
Рисунок 2 — Среднее время выполнения задания

Литература:

1 Эвристики распределения задач для брокера ресурсов Grid [Электронный ресурс] / А.И. Аветисян [и др.] . – [2009]. – Режим доступа : http://www.citforum.ru/nets/digest/grid/index.shtml

2 Имитационное моделирование грид-систем : монография / Лукьянов В.С., Андреев А.Е., Жариков Д.Н., Островский А.А., Гаевой С.В.; ВолгГТУ. - Волгоград, 2012. - 215 с.

3 Имитационная модель гетерогенной вычислительной системы / В.С. Лукьянов, Д.Н. Жариков, С.В. Гаевой, Д.С. Попов // Изв. ВолгГТУ. Серия "Актуальные проблемы управления, вычислительной техники и информатики в технических системах". Вып. 11 : межвуз. сб. науч. ст. / ВолгГТУ. - Волгоград, 2011. - № 9. - C. 85-88.

4 Свид. о гос. Регистрации программы для ЭВМ № 2010610693 от 20 янв. 2010 г. РФ, МПК (нет). Имитационная модель грид-системы (GridModel) / В. С. Лукьянов, Д. Н. Жариков, С. В. Гаевой, Ю. В. Шафран; ВолгГТУ. - 2010.

5 Интернет-портал по грид-технологиям :: GRIDCLUB.RU [Электронный ресурс]. – [2011]. – Режим доступа : http://gridclub.ru/

6 Проблемы моделирования GRID-систем и их реализация [Электронный ресурс] / О. И. Самоваров [и др.] // Портал «Информационно-коммуникационные технологии в образовании». – [2010]. – Режим доступа : http://www.ict.edu.ru/vconf/files/9451.pdf

7 Logs of Real Parallel Workloads from Production Systems [Электронный ресурс] // The Rachel and Selim Benin School of Computer Science and Engineering. – [2013]. – Режим доступа : http://www.cs.huji.ac.il/labs/parallel/workload/logs.html

8 Фоменков, С. А. Моделирование систем [Электронный ресурс] / С. А. Фоменков. – Волгоград, [2004]. – 1CD-ROM

9 Шеннон, Р. Имитационное моделирование систем – искусство и наука / Р. Шеннон ; пер. с англ. под ред. Е. К. Масловского. – М. : Мир, 1978. – [418 c.]