Піменов Д. О.

Бердянський державний педагогічний університет

Вивчення процесів у реальних та ідеальних газах із застосуванням комп’ютерної графіки

При вивченні процесів у реальних та ідеальних газах виникає необхідність у графічному їх відображенні та у розрахунку термодинамічних параметрів і потенціалів. Наявність графічних ілюстрацій процесів, які представлені у будь-яких термодинамічних координатах сприяє більш глибокому розумінню фізики процесу. У зв’язку з цим визначена мета даної роботи: написання інтерактивного програмного забезпечення для вивчення процесів у реальних та ідеальних газах.

У створеному програмному забезпеченні можливо моделювати процеси з реальними та ідеальними та газами у таких системах координат: PV, VT, PT, ST. Систему координат обирає користувач за допомогою перемикачів, які розташовані на панелі інструментів. Також він обирає тип газу, кількість речовини та інші початкові параметри.

Графік процесу, який вивчається з ідеальним або реальним газом, створюється за допомогою маніпулятора миші наступним чином. Користувач, рухаючи його з затисненою лівою кнопкою, моделює графічне зображення процесу, який відбувається з газом. Натиснувши праву кнопку миші можливо замкнути створений процес. При цьому координати курсору миші (припустимо P і V) потрапляють до масиву. Виразив температуру T із рівняння Клапейрона – Менделєєва для ідеальних газів або з рівняння Ван-дер-Ваальса для реальних газів, отримаємо третій параметр стану газу. Таким чином, маючи масив із PVT координат, ми можемо перебудувати намальований маніпулятором миші графік процесу в інші можливі термодинамічні 2D або 3D координати.

У програмі можливо для конкретного газу та конкретно заданого процесу розрахувати усі термодинамічні потенціали (внутрішню енергію - U, ентропію - S, ентальпію - H, енергію Гіббса - G, вільну енергію Гельмгольца F ) за відомими формулами та графічно представити їх у вигляді залежностей від термодинамічних параметрів (тиску - p, об’єму - V, температури – T ).

Діалоговий інтерфейс програми дозволяє відкрити, зберегти та роздрукувати створені та перебудовані графіки залежностей, побачити та записати у файл значення усіх термодинамічних параметрів та потенціалів у кожній точці процесу, їх максимальні та мінімальні значення.

Можливості програми проілюструємо на наступних прикладах.

1. Побудуємо ізобару (синій колір) та ізохору (зелений колір) в PV системі та перебудуємо у ST систему. Отримаємо результат, який зображений на рис. 1.

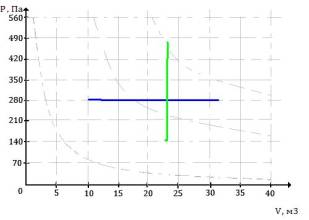
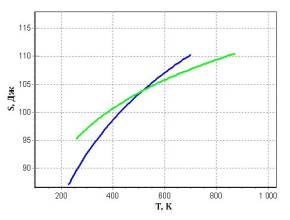
Рис 1. Ізобара та ізохора у PV і ST системах координат.

Із рисунку 1 у ST системі бачимо, що ізобара більш швидше зростає ніж ізохора, оскільки при ізобарному процесі вся кількість теплоти наданій системі ∂Q=TdS витрачається на збільшення її внутрішньої енергії dU та на здійснення роботи ∂A, а при ізохорному - тільки на збільшення внутрішньої енергії dU.

2. Термодинамічний потенціал Гіббса G - функція стану системи, яку визначається наступним чином: Її повний диференціал дорівнює:

Як бачимо, термодинамічний потенціал G можна розглядати як характеристичну функцію параметрів (p,T) звідки випливає, що

; .

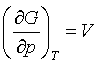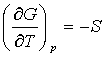Якщо T і p залишаються сталими, маємо нерівність: , звідки випливає, що необоротний процес у системі за цих умов супроводжується зменшенням її термодинамічного потенціалу, який в рівноважному стані є мінімальний. Переконаємося у цьому.

Змоделюємо у програмі ізотерму в VT системі, збільшуючи об’єм, та перебудуємо в Gp систему координат (рис. 2).

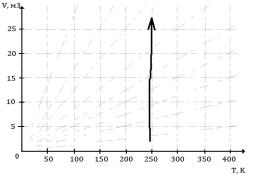
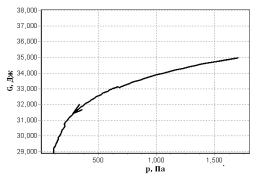
Рис. 2 Умови рівноваги та стійкості

Згідно з виразом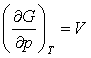, перша похідна від енергії Гіббса за тиском при постійній температурі позитивна та дорівнює об’єму V. Отже, залежність енергії Гіббса від тиску при постійній температурі зростаюча. Друга похідна - від’ємна. Отже функція f=G(p) є впуклою. Так і є.

Процес на рисунку 2 супроводжується зменшенням потенціалу Гіббса, а отже система прагне до рівноваги.

Висновок: створена комп’ютерна програма сприяє більш глибокому та швидкому сприйняттю розділів фізики пов’язаних з властивостями реальних та ідеальних газів.

Література

1. Архангельский А. Я. Программирование в С++ Builder 6./ А. Я. Архангельский – М.: «Издательство БИНОМ» 2003 г. – 1152 с.

2. Школа О.В. Основи термодинаміки і статистичної фізики: навчальний посібник [для студ. вищ. навч. закл.] / О.В.Школа. – Донецьк: Юго – Восток, 2009. – 375 с.