Физика/ 1. Теоретическая физика

Ст. преподаватель Гасанова С.А.

Мценский филиал ФГБОУ ВПО «Государственный университет – учебно-научно-производственный комплекс»

О прохождении волны через систему пластин в состоянии их адгезии

Существует проблема теоретического обоснования неразрушающего контроля адгезионного соединения тонкопленочного покрытия с основой, на которую оно нанесено. Один из вариантов – оценка интенсивности отраженного от поверхности раздела сигнала, направленного к ней со стороны свободной поверхности. Учитывая важность сплошности соединения и возможность наличия ее нарушения микроскопических размеров, при этом желательно использовать волны очень короткой длины. Такие волны можно инициировать с помощью рентгеновского облучения свободной поверхности [1]. При этом проблема осложняется тем, что в нанометровом диапазоне длин дисперсионный закон для таких волн перестает быть линейным. Кроме того, должна существовать модель упругой среды в достаточной степени адекватно отражающая механическое поведение материалов, находящихся в состоянии адгезии. Для теоретического рассмотрения ситуации предлагается использовать вариант линейной теории упругости изотропных, однородных материалов второго порядка, предложенный в работе [2]. Выбор теории обусловлен тем, что, как показано в [2], в ее рамках существует возможность описания, как дисперсионного закона, так и адгезионного контакта. Последний рассматривается как вариант сопряжения полей напряжений, перемещений и, в дополнение к классическому жесткому контакту, – их градиентов, возникающих в контактирующих телах при адгезии. В данной работе в качестве примера рассматривается одномерный вариант теории, в которой учитываются деформации и перемещения частиц контактирующих тел только в направлении нормали к плоскости контакта пленки и основы. Задача о распределении продольных перемещений вдоль оси , ориентированной перпендикулярно плоскости контакта тел с номерами в любой момент времени в отсутствии внешних воздействий имеет вид:

, j = 1: (1)

j = 2:

, х = h⁽¹⁾, х = - h⁽²⁾ (2)

, х = h⁽¹⁾, х = - h⁽²⁾ (3)

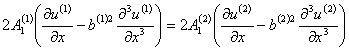, х = 0 (4)

, х = 0 (5)

, х = 0 (6)

, х = 0 (7)

В этой системе: – скорость распространения малых продольных возмущений в материале пластины с номером ; , – его коэффициенты Ламэ материала пластины; – дополнительная константа, характеризующая неклассическое свойство материала оказывать сопротивление приобретению не только относительной деформации, но и ее градиента; – также дополнительная постоянная величина, характеризующая начальное напряженное состояние среды, способное совершать работу на градиентах относительных деформаций.

Уравнения (1) при превращаются в известные одномерные классические волновые уравнения. Условия (2) и (3) означают отсутствие на свободных поверхностях пластин классических поверхностных нагрузок, способных совершать работу на перемещениях точек своего воздействия и на их градиентах соответственно. Условия (4) – (7) – это условия сопряжения. Условия (4) и (5) означают непрерывность нормальных к поверхности контакта составляющих классического тензора напряжений, для которого обобщенным перемещением является классический тензор деформации, и неклассического тензора напряжений, для которого обобщенным перемещением является тензор, являющийся вторым градиентом вектора перемещений. Условия (6) и (7) – это кинематические условия полей перемещений и их производных по нормали к поверхности контакта соответственно.

В соответствии с этой постановкой нарушение адгезии означает переход от условий сопряжения системы (1), соответствующих адгезионному контакту, к одному из следующих условий, заменяющих соответствующие в системе (1):

– вместо (5) и (7) означает переход к классическому жесткому контакту в рамках неклассической теории упругости. Добавление к этому условию требования

, х = 0

– вместо (4) и (6) означает потерю контакта между пластинами, то есть расслоение их системы.

Как и в классическом случае, волновое уравнение (1), в силу своей линейности, допускает общее решение, являющееся линейной комбинацией базисных, частных. Одно из таких базисных решений имеет вид:

(8)

Для определения постоянных интегрирования , ; , , используются начальные и краевые условия.

Вид выражения (8) совпадает с классическим за исключением первых двух слагаемых в квадратных скобках. Учитывая, что параметр очень мал (имеет порядок [2]) и стоит при старшей производной, можно утверждать, что эти слагаемые описывают пограничный слой вблизи граничных плоскостей пластины, имеющий толщину порядка величины этого параметра. Это означает, что решение волнового уравнения (1) уже на очень небольшом расстоянии от границ пластины по форме полностью совпадает с классическим с той лишь разницей, что волновое число связано с частотой колебаний более сложной, чем линейная, зависимостью.

;

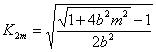
Величина параметра определяется при решении соответствующей задачи о поиске собственных функций и собственных чисел. Например, при условии отсутствия внешних воздействий на граничных плоскостях исследуемой пластины толщиной уравнение для поиска этого параметра имеет вид:

,

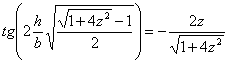Отсюда следует, что для анализа качества адгезионного соединения можно попытаться использовать только классические формы решения сопряженной одномерной задачи о продвижении сигнала через систему двух пластин.

Классическое решение представляет еще практический интерес по следующим обстоятельствам. Если состояние адгезионного контакта проверяется путем пропускания через него продольных плоских волн, распространяющихся от свободной поверхности покрытия по нормали к ней, то, рассматривая в качестве эталонного случай классического жесткого контакта, следует ожидать, что при полном расслоении покрытия и основы интенсивность отраженного от поверхности контакта сигнала окажется больше расчетной. В то время как в случае полной адгезии от граничной поверхности будет отражаться часть сигнала меньшей интенсивности ввиду того, что с физической точки зрения в последнем случае атомная решетка одного тела является продолжением другой, а в первом случае связь между ними полностью нарушена.

Данные теоретические рассуждения позволяют построить теоретическую базу метода неразрушающего контроля качества поверхности адгезионного контакта тонкопленочного покрытия посредством пропускания через покрытие волн с длиной в нанометровом диапазоне и регистрации отраженного от поверхности контакта сигнала. Реализуемая в практических условиях регистрация сигнала дает возможность сравнить его с расчитанным теоретически на основании классической теории. По степени их рассогласования можно судить о качестве адгезионного контакта.

Список литературы

1. Киттель Ч. Введение в физику твердого тела. – М.: Наука, 1978. – 792 с.

2. Шоркин В. С. Модель сплошной упругой среды, основанная на представлении о дальнодействующем потенциальном взаимодействии ее частиц // Упругость и неупругость. Под ред. И. А. Кийко, Р.А. Васина, Г. Л. Бровко. – М.: Ленанд, 2006. – С. 271 – 282.

3. Горелик С.С. Материаловедение полупроводников и диэлектриков. / C.С. Горелик, М.Я. Дашевский // М.: Металлургия, 1988. – 576 с.

4. Горшков А.Г. Медведский А.Л. Рабинский Л.Н., Тарлаковский Д.В. Волны в сплошных средах. – М.: ФИЗМАТЛИТ, 2004. –472 с.

5. Гурский Д.А., турбина Е.С. Вычисления в MathCAD 12. – СПб.: Питер, 2011. – 544 с.

6. Карташев А.П., Рождественский Б.Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. – М.: Наука, 1986. – 272 с.