Строительство и архитектура/5. Теплогазоснабжение и вентиляция
к.т.н. Зиганшин А.М., студ. Минязова Р.И., студ. Самиева А.Ж.
Казанский государственный архитектурно-строительный университет, Россия
Тестирование численной
модели для задачи о течении в отводе на 90°
При исследовании гидро- и аэродинамических задач сейчас очень широко используется численный эксперимент. При этом могут использоваться как программные коды специально созданные для решения конкретных задач, так и более универсальные вычислительные комплексы. Программы первого класса обычно хорошо описывают течения для моделирования которых были разработаны, но достаточно сложны в использовании, и практически не универсальны. Второй класс программных средств имеет специально разработанный интерфейс, позволяющий решать широкий класс задач даже без глубоких знаний математических алгоритмов и физических моделей. Это достигается использованием наиболее опробованных, достоверных и универсальных моделей, а также эмпирических констант служащих для их настройки. При этом обычно такие вычислительные комплексы содержать достаточно большой выбор таких моделей. Это приводит к необходимости предварительной настройки вычислительного комплекса. Наиболее правильно проводить такую настройку путем сравнения результатов получаемых при численном расчете с ранее известными результатами достоверных экспериментальных исследований.
В статье проводится тестирование (настройка, подбор) численной модели при решении задачи о течении воздуха в двухмерном канале с резким отводом на 90°. Такого рода возмущающие элементы (ВЭ) хорошо исследованы с точки зрения их сопротивления. Имеются подробные данные о коэффициенте местного сопротивления (КМС) этого ВЭ найденные экспериментально [1].
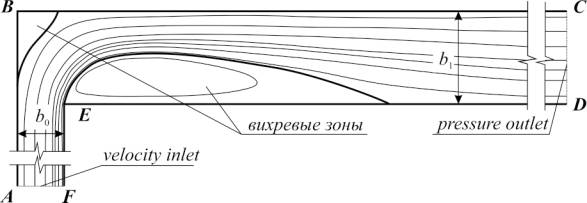
Рис. 1 Геометрия и линии тока течения в канале с отводом
Ширина исследуемого канала (рис.1) до поворота b0 = 0,1м, а после – b1 = 0,2м. По границе AF задается условие входного потока воздуха с равномерным профилем скорости – “velocity inlet”, граница CD – свободный выход (“pressure outlet”, избыточное давление равно нулю). Остальные границы непроницаемы. Длина прямых участков взята достаточной для исключения влияния граничных условий – 40 b0 до ВЭ и 80 b1 после. Задача решается в турбулентной постановке: vвх = 68м/с, Re вх = 3,8·105. В справочнике [1] приведен, найденный экспериментально, коэффициент местного сопротивления для такого случая: ζ = 0,55.
В работе исследуется влияние на течение используемых при
решении моделей турбулентности и пристеночных функций. В качестве моделей
турбулентности выбраны три разновидности наиболее универсальной k-ε модели
турбулентности – «Standard»,
«RNG» и «Realizable», а также модель
турбулентности «Рейнольдсовых напряжений» (RSM). Для каждой модели были решены задачи с тремя видами
пристеночных функций – «Стандартные пристеночные функции» (SWF), «Неравновесные пристеночные
функции» (NeWF),
«Расширенное пристеночное моделирование» (EWT) [2]. Задача решается при помощи вычислительного комплекса Fluent.
На первом этапе было проведено устранение сеточной зависимости – путем последовательного измельчения сетки сначала во всей расчетной области (до размеров ячейки – 6мм), а затем в пристеночной области (до размеров ячейки – 0,1 мм). Проверка по безразмерному параметру y* (~ 30) показывает, что сетка вблизи твердых границ достаточно мелкая для правильно моделирования течения в погранслое [2].
Далее с использованием последней сетки было проведено решение вариантов задач с комбинацией разных моделей турбулентности и пристеночных функций. В результате решения вычислительным комплексом определяется весь набор параметров течения. С точки зрения исследования сопротивления ВЭ наиболее интересными представляются линии тока, по которым можно определить очертания вихревых зон, образующихся при срыве с острых кромок в отводе, а также поле распределения полного давления в отводе, которое позволяет определить коэффициент местного сопротивления отвода.
При определении вихревых зон используется понятие граничной или свободной линии тока – линии тока отделяющей область вихревого движения в отрывной зоне от основного течения (рис.1). Граничные линии тока по результатам численного решения строятся как изолинии двух крайних (наибольшее и наименьшее) значений функции тока на выходной границе. Такой способ позволяет определить положение отрывных зон с точностью до размеров ячейки расчетной сетки в приграничной области (~0,1мм).
На рис.2 представлены результаты определения очертаний вихревых зон для рассчитанных задач.
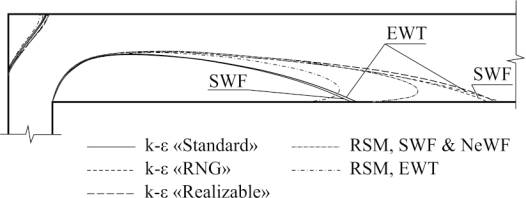
Рис.2 Очертания вихревых зон
На рисунке видно образование двух отрывных зон: во внешнем углу отвода, а также при срыве потока с острой кромки отвода (у внутреннего угла). Отрывная зона в углу невелика, и различие в зависимости от используемых моделей также несущественно. Зона у внутреннего угла гораздо больше, как и влияние используемых моделей.
Видно, что выбор модели турбулентности достаточно сильно влияет на размеры и очертания вихревой зоны. В то время как влияние пристеночного моделирования не так однозначно – для всех разновидностей k-ε модели турбулентности очертание вихревой зоны слабо зависит от использованного пристеночного моделирования. В то же время для модели RSM применение пристеночных функций (SWF или NeWF) или использование расширенного пристеночного моделирования (EWT) приводит к получению существенно различающихся результатов. Причем результаты, полученные при использовании сочетания стандартной k-ε модели со стандартными пристеночными функциями и сочетания модели RSM и EWT приводит к получению схожих по очертанию вихревой зоны результатов.
С использованием полученных в результате решения полей полного давления были рассчитаны коэффициенты местного сопротивления для каждого варианта сочетания исследуемых моделей, при этом использовалась методика, описанная в [3].
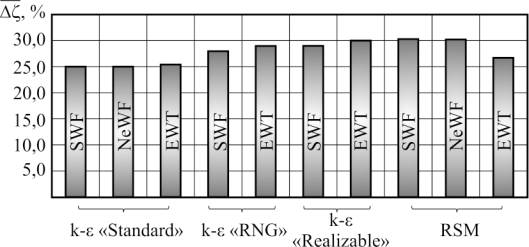
Рис. 3
Результаты представлены в виде графика, на котором по оси
абсцисс указаны используемые модели, а по оси ординат – ![]() относительное отличие
КМС полученного при численном решении от КМС указанного в [1].
относительное отличие
КМС полученного при численном решении от КМС указанного в [1].
Видно, что наилучшее приближение к известному результату получается при использовании сочетания стандартной k-ε модели со стандартными пристеночными функциями (~25%) и несколько хуже сочетания модели RSM и EWT (~27%).
Литература:
1. Идельчик И. Е. Справочник по гидравлическим сопротивлениям/ Под ред. М. О. Штейнберга. — 3-е изд., перераб. и доп.— М.: Машиностроение, 1992. — 672 с.
2. ANSYS FLUENT 6.3 Documentation / 12.10.2 Standard Wall Functions. [Электронный ресурс]. URL: https://www.sharcnet.ca/Software/Fluent6/html/ug/node512.htm (дата обращения: 04.11.2013).
3. Посохин, В.Н. К определению коэффициентов местных сопротивлений возмущающих элементов трубопроводных систем / В.Н. Посохин, А.М. Зиганшин, А.В. Баталова // Известия высших учебных заведений. Строительство. – 2012.– №9 . – С. 108-112.