Асистент Васько А.І., студент Долик Р.М.

Івано-Франківський Національний технічний університет нафти і газу, Україна

ДО ПИТАННЯ ВИКРИВЛЕННЯ СВЕРДЛОВИН В АНІЗОТРОПНИХ ПОРОДАХ

Характер викривлення свердловин залежить від співвідношення відхиляючої та випрямляючої сил, які діють на долото.

Різна жорсткість і вага одиниці довжини окремих ділянок колони будуть впливати на форму її пружної осі та вектора навантаження на вибій.

Розглянемо рисунок 1, на якому векторами V та F позначені відповідно вертикальна та горизонтальна компоненти реакції вибою свердловини на долото, а пряма d показує напрямок, перпендикулярний площинам нашарувань і утворюючий із вертикаллю кут .

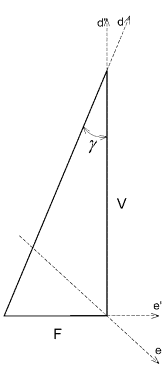
Рисунок 1 – Розрахункова схема

Проектуємо реакцію вибою свердловини на вісь d та перпендикулярну їй компоненту, перпендикулярну площинам нашарування: і компоненту, перпендикулярну площинам нашарування .

Можна записати, що компонента митт’євого переміщення в напрямку, перпендикулярному площинам нашарування, тобто вздовж вісі, рівна:

, (1)

де - коефіцієнт пропорційності.

Припустимо, що компонента переміщення в напрямку «е» для анізотропних порід менша, ніж для порід ізотропних. Тоді ця компонента може бути записана наступним чином:

, (2)

де - додатна величина, менша одиниці.

По визначеннях індекс анізотропії дорівнює:

, (3)

Проектуючи обидві компоненти переміщення на вертикальну вісь «d´» і горизонтальну вісь «е´», отримаємо вертикальну компоненту переміщення:

, (4)

та горизонтальну компоненту переміщення:

, (5)

Отже, якщо - кут нахилу напрямку переміщення, тоді можна записати, що дорівнює відношенню горизонтальної компоненти до вертикальної. Далі, вважаючи що кут малий і тому , а також підставивши замість величину , отримуємо після перетворень:

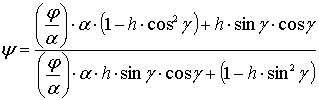, (6)

і для умов рівноваги :

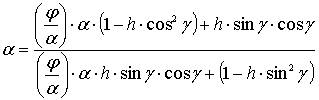, (7)

Анізотропні горизонтально залеглі породи.

Для анізотропних горизонтально залеглих порід , тому формула (7) для умов рівноваги приймає вигляд:

, (8)

Тоді як для ізотропних порід .

Анізотропні похило залеглі породи

Для анізотропних похило залеглих порід були отримані залежності зміни зенітного кута викривлення свердловини від кута нахилу пластів, індексу анізотропії, режимно-технологічних параметрів та геометричних розмірів колони. Пояснимо, як були отримані дані залежності. Для любої даної кривої індекс анізотропії , кут нахилу пластів та безрозмірне осьове навантаження являються постійними та відомими величинами. Отже, змінними в рівнянні (7) будуть і .

Виберемо довільно декілька значень . Відповідні значення можна легко отримати з графіка. Тепер рівняння (7) містить лише одну змінну , відносно якої воно і вирішується.

Таким чином, для кожного довільно вибраного значення була отримана відповідна величина . Нарешті, діленням на були знайдені значення , що по вісі абсцис на графічних залежностях, і відшкодувати величину , а не зазор 2. Графічні залежності будуть справедливі лише для значень , які відповідають певним діаметрам обважнених труб, а для інших розмірів ці графіки будуть давати лише наближені рішення.

Щоб переконатися в стабільності умов рівноваги на графічних залежностях, перетворимо формулу (6) наступним чином:

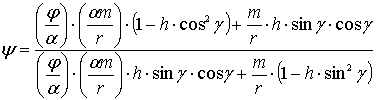, (9)

Припустимо, як і раніше, що значення , та являються постійними. Задамося також діаметрами обважнених труб та свердловини. Отже, відношення також буде відоме і постійне. Виберемо довільно значення . Відповідні їм величини отримаємо із залежностей, а значення визначимо за формулою (9). З цих розрахунків було визначено, що для умов рівноваги, тобто для

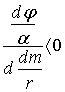
Це означає, що рівновага стійка.

Криві на графічних залежностях показують, що рівноважний кут мінімальний при деяких значеннях зазору, які в більшості випадків не виходять за межі діапазону зазорів в реальних умовах буріння. Якщо зазор менше вказаних значень, рівноважний кут збільшується. Але такий висновок не залежить від довільного уявлення про «анізотропію» з точки зору буріння.

В похило падаючих пластах сила, прикладена до долота, напрямлена так, що вона прагне відхилити свердловину до вертикалі, отже, відношення менше одиниці.

Розглянемо в такому випадку умови, виражені точкою, в якій значення осьового навантаження на долото і відношення ті ж, що і в попередньому випадку.

Припустимо, що і кут нахилу свердловини той же самий. Отже, кути нахилу сили, яка діє на долото ті ж самі. Так як величина і напрямок сили, яка діє на долото та породу, одинакові, можна зробити висновок, що і рівноважні кути в обох випадках одинакові.

Полого падаючі породи

При малому значенні в формулі (6) можна замість підставити , а замість - одиницю, тоді нехтуючи значеннями та як величинами малими в порівнянні з одиницею, отримаємо:

, (10)

і для умов рівноваги ():

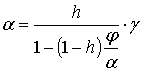, (11)

Література.

1. Калинин А.Г. Бурение наклонных и горизонтальных скважин. /А.Г. Калинин, Б.А. Никитин, К.М. Солодкий, и др. - М.: Недра, 1997. – 648с.

2. Мислюк М.А. Буріння свердловин: довідник. /М.А.Мислюк, І.Й. Рибчич, Р.С. Яремійчук. – К.: Інтерпрес ЛТД, 2004. – 292с. – т.3. – Вертикальне та скероване буріння.

3. Вудс Г. Искривление скважин при бурении. /Г. Вудс, А. Лубинский – М. Гостоптехиздат, 1960. – 161с.