Аспирант Лазаренко М.Л
Московский государственный университет
природообустройства (МГУП).
СИНТЕЗ РОБАСТНЫХ СИСТЕМ С
ШИРОТНО-ИМПУЛЬНОЙ
МОДУЛЯЦИЕЙ УПРАВЛЯЮЩИХ ВОЗДЕЙСТВИЙ
Одной из главных проблем при создании автоматических систем является
все возрастающая сложность управляемых технологических процессов, обусловленная
разнообразием взаимодействий между материальными и энергетическими потоками
объектов и окружающей их среды. Это приводит к появлению различных
неопределенностей, вследствие неполноты информации об указанных взаимодействиях.
Необходимо отметить, что немало математически изящных теорий в области
технических систем автоматического управления не получили практического
применения, т.к. нуждались в весьма детальной и труднодоступной информации о
статистических характеристиках возмущений, действующих на управляемые объекты.
Осознание причины неудач привело к созданию методов робастного
управления технологическими процессами, доказавшими на практике свою высокую
эффективность в условиях информационной неопределенности, т.е. при неполноте
или отсутствии информации об указанных статистических характеристиках [1].
Эффективность
робастных систем обеспечивается их настройкой на высокое быстродействие, что
позволяет им успешно парировать возмущения с различными статистическими
характеристиками.
Согласно
работам [2, 3] повышение быстродействия замкнутых систем управления обеспечивается
при максимизация свободного члена их характеристического уравнения![]() , т.е. выбор параметров настройки регулятора выполняется таким
образом, чтобы выполнялось требование
, т.е. выбор параметров настройки регулятора выполняется таким
образом, чтобы выполнялось требование
![]() .
(1)
.
(1)
Наряду с
требованием (1) используются также следующие ограничения на запас устойчивости
замкнутой системы [4]:
![]() ; (2)
; (2)
![]()
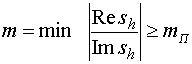 , (3)
, (3)
![]()
где ![]() и
и ![]() – показатели относительного и абсолютного
демпфирования свободного движения замкнутой системы соответственно, а
– показатели относительного и абсолютного
демпфирования свободного движения замкнутой системы соответственно, а ![]() и
и ![]() – их предельно допустимые значения;
– их предельно допустимые значения; ![]() ,
, ![]() – корни
характеристического уравнения;
– корни
характеристического уравнения; ![]() – порядок этого уравнения.
– порядок этого уравнения.
В работах [1, 4] показано, что
требование (1) при ограничениях (2) и (3) выполняется в случае расположения
корней ![]() ,
, ![]() характеристического уравнения в заданном положении
характеристического уравнения в заданном положении
![]() (4)
(4)
где
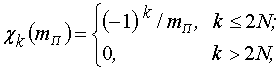
а ![]() -
целая часть отношения
-
целая часть отношения ![]() .
.
Отметим,
что выполнение требований (4) можно обеспечить лишь в тех случаях, когда объект
полностью управляем и имеется полная обратная связь по состоянию замкнутой
системы, т.е. при формировании сигнала обратной связи используются все координаты
вектора состояния ![]() .
.
Одна из проблем, с которыми приходится
сталкиваться при настройке систем управления технологическими процессами,
заключается в отсутствии полной обратной связи по вектору состояния ![]() Это объясняется тем,
что управляемые объекты зачастую описываются дифференциальными уравнениями
высоких порядков, а в алгоритмах (законах) управления обычно не удается
использовать производные по времени от вектора
Это объясняется тем,
что управляемые объекты зачастую описываются дифференциальными уравнениями
высоких порядков, а в алгоритмах (законах) управления обычно не удается
использовать производные по времени от вектора ![]() выше первого порядка,
т.к. наряду с полезным сигналом он содержит и шумовые составляющие, влияние
которых недопустимо усиливается с возрастанием порядка дифференцирования по
времени.
выше первого порядка,
т.к. наряду с полезным сигналом он содержит и шумовые составляющие, влияние
которых недопустимо усиливается с возрастанием порядка дифференцирования по
времени.
Кроме того, управляемым объектам нередко
присуща пространственная распределенность параметров, а вектор состояния
системы с таким объектом имеет бесконечную размерность. Разумеется, на практике
невозможно реализовать обратную связь по бесконечному числу координат вектора ![]() .
.
Поэтому в системах с неполной обратной связью по состоянию не все корни
характеристического уравнения можно расположить в любом, наперед заданном
положении, т.е. обеспечить выполнение требований (4).
При данных обстоятельствах приходиться
ограничиться выполнением требований (4) лишь для так называемых доминирующих
корней системы.
Предположим, что система имеет ![]() доминирующих корней
доминирующих корней ![]() ,
,
![]() тогда для остальных корней системы
тогда для остальных корней системы ![]() ,
,
![]() должны выполняться неравенства
должны выполняться неравенства
![]() ; (5)
; (5)
![]() . (6)
. (6)
В соответствии с условием (5) все
недоминирующие корни должны располагаться на комплексной плоскости не ближе к
мнимой оси, чем доминирующие.
Условие (6) означает, что недоминирующие корни
расположены значительно дальше от начала системы координат по сравнению с
доминирующими.
При выполнении условий (5) и (6) качество
управления определяется в основном доминирующими корнями и поэтому выполнение
для них требований (4) позволяет значительно повысить качество управления
технологическими процессами.
Поэтому при оптимизации систем с неполной
обратной связью по состоянию, а к ним заведомо относятся системы с распределенными
параметрами, требования (4) должны выполняться лишь для доминирующих корней,
т.е. в выражении (4) необходимо величину ![]() (число корней системы) заменить на
(число корней системы) заменить на ![]() (число доминирующих корней). В таком случае
это выражение принимает вид
(число доминирующих корней). В таком случае
это выражение принимает вид
![]() ;
; ![]() . (7)
. (7)
При
расположении доминирующих корней в соответствии с требованиями (7) минимизируются
значения АЧХ замкнутых систем в интервале частот ![]() ,
что обеспечивает оптимизацию фильтрующих свойств этих систем в указанном
интервале.
,
что обеспечивает оптимизацию фильтрующих свойств этих систем в указанном
интервале.
Исследования также показали
[4], что значение величины ![]() в робастных системах определяется количеством
параметров настройки
в робастных системах определяется количеством
параметров настройки ![]() используемого регулятора,
т.е.
используемого регулятора,
т.е. ![]() .
.
Кроме
того, согласно [4] значение частоты ![]() для нечетных значений
для нечетных значений
![]() определяется при
решении следующего уравнения:
определяется при
решении следующего уравнения:
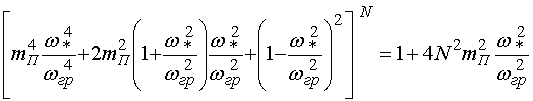 , (8)
, (8)
где ![]() , а собственная частота системы
, а собственная частота системы ![]() определяется равенством
определяется равенством ![]() .
.
Для
четных значений ![]() граничная частота
граничная частота ![]() удовлетворяет уравнению
вида
удовлетворяет уравнению
вида
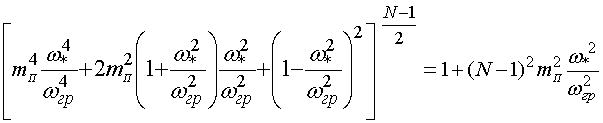 . (9)
. (9)
Таким
образом, решая уравнения (8), (9) для любых регуляторов можно выразить значение
граничной частоты ![]() через собственную
частоту системы
через собственную
частоту системы ![]() , которая обычно
близка к резонансной частоте и ее значение устанавливается при настройке
системы.
, которая обычно
близка к резонансной частоте и ее значение устанавливается при настройке
системы.
Нередко на практике приходиться
использовать исполнительные механизмы с постоянной скоростью перемещений, или
нагревательные устройства с неизменной мощностью. В таких случаях приходиться
использовать широтно-импульсную модуляцию (ШИМ), когда длительность
управляющего сигнала постоянной амплитуды ![]() может изменяться в
течение периодов времени
может изменяться в
течение периодов времени ![]() , как показано на рис. 1.
, как показано на рис. 1.
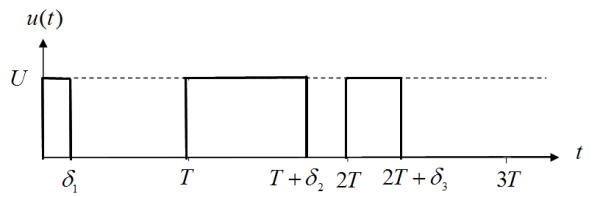
Рис. 1.
Широтно-модулированный сигнал управления ![]() :
: ![]() – период
следования
– период
следования
импульсов; ![]() – амплитуда
импульсов;
– амплитуда
импульсов; ![]() ,
, ![]() и
и ![]() – длительности
импульсов.
– длительности
импульсов.
Определим
оптимальное значение периода ![]() для робастных систем управления.
для робастных систем управления.
Учтем,
что ввиду инерционности исполнительного органа всегда существует некоторое
минимально возможное значение длительности импульсов ![]() , показанных на рис. 1,
которое обозначим как
, показанных на рис. 1,
которое обозначим как ![]() .
.
На временном интервале [0, ![]() ] разложим функцию
] разложим функцию ![]() в комплексный ряд Фурье
в комплексный ряд Фурье
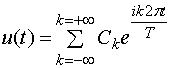 ,
(10)
,
(10)
где
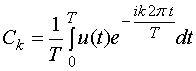 =
=  =
=
=  . (11)
. (11)
С учетом
выражения (11) имеем
![]() =
= 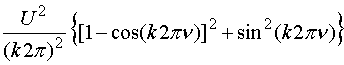 ,
, ![]() , (12)
, (12)
где ![]() – комплексно
сопряженное значение величины
– комплексно
сопряженное значение величины ![]() , а
, а
![]() .
(13)
.
(13)
Определим
максимум квадрата модуля ![]() комплексного коэффициента
комплексного коэффициента ![]() в зависимости от скважности
импульсов
в зависимости от скважности
импульсов ![]() . Для этого продифференцируем величину
. Для этого продифференцируем величину ![]() по
по ![]() и приравняем
полученное выражение нулю. С учетом (12) получим следующее уравнение:
и приравняем
полученное выражение нулю. С учетом (12) получим следующее уравнение:
![]() . (14)
. (14)
Принимая
во внимание равенство (13) решения уравнения (14) представим в виде
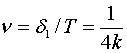 ,
, ![]() = 1, 2, 3, … .
(15)
= 1, 2, 3, … .
(15)
Выражение
(15) устанавливает значения скважностей импульсов ![]() при которых достигаются
максимумы квадратов амплитуд
при которых достигаются
максимумы квадратов амплитуд ![]() гармоник с номерами
гармоник с номерами ![]() , т.е. максимизируется мощность
, т.е. максимизируется мощность ![]() управляющих
воздействий на частотах
управляющих
воздействий на частотах
![]() ,
, ![]() = 1, 2, 3, … ,
(16)
= 1, 2, 3, … ,
(16)
причем для всех частот ![]() выполняется
неравенство
выполняется
неравенство
![]() ,
, ![]() = 1, 2, 3, … , (17)
= 1, 2, 3, … , (17)
Согласно
(17) когда
![]() ,
(18)
,
(18)
то имеют место следующие неравенства:
![]() ,
, ![]() = 1, 2, 3, … ,
= 1, 2, 3, … ,
указывающие на то, что в интервале частот оптимальной
фильтрации ![]() мощность управляющих воздействий максимальна, что
обеспечивает наиболее эффективное подавление возмущений робастными системами
управления.
мощность управляющих воздействий максимальна, что
обеспечивает наиболее эффективное подавление возмущений робастными системами
управления.
Таким
образом, выполненные исследования позволили определить оптимальные значения
характеристик ШИМ для робастных систем, что должно способствовать более эффективному
управлению технологическими процессами.
Литература
1. Шавров А.В., Солдатов
В.В. Многокритериальное управление в условиях статистической неопределенности.
– М.: Машиностроение, 1990.
2. Ротач В.Я. Теория автоматического управления:
Учебник для вузов. – М.: Изд-во МЭИ, 2004.
3. Шавров А.В., Коломиец
А.П. Автоматика: Учебник для вузов. – М.: Колос, 1999.
4. Солдатов
В.В., Дидманидзе О.Н., Судник Ю.А. Управление техническими системами в условиях
информационной неопределенности. Под ред. В.В. Солдатова. – М.: изд-во «УМЦ»Триада».