УДК 628.16:621.981.3
Тришевский
О.И. докт. техн. наук, проф.
Салтовец
Н.В., инж.
Национальный технический университет сельского хозяйства им.П.Василенко,
г.Харьков, Украина
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕПЛОВОГО СОСТОЯНИЯ СИСТЕМЫ ВАЛОК-ПОЛОСА ПРИ ГОРЯЧЕЙ ПРОКАТКЕ
Стоящая
на протяжении ХХ столетия задача наращивания объёмов выпуска прокатной
продукции потребовала от металлургов неоднократного изменения и усовершенствования
применяющихся технологий горячей прокатки листа. В соответствии с этими
задачами увеличивались и совершенствовались и системы водоснабжения прокатных
станов. Экономический кризис 90-х годов прошлого века обусловил появление
технологий, обеспечивающих существенное сокращение затрат на производство продукции.
Анализ
отечественной и зарубежной технической литературы [1-4] показал, что на сегодняшний
день вследствие отсутствия единого мнения по поводу тепловых процессов, имеющих
место на прокатных станах, конструктивное выполнение систем подачи воды для
охлаждения валков и полосы отличается значительным разнообразием, недостаточной
обоснованностью использования отдельных схем и требует дальнейшего усовершенствования.
Для
оценки возможности реконструкции и совершенствования систем водоснабжения по
критерию энергетических затрат необходимо иметь научно обоснованную методику
расчёта количества воды, которое будет использоваться при той или иной новой
технологии. Традиционно количество воды для систем водоснабжения прокатных
станов определяли на основе натурных экспериментов на существующем
оборудовании. Это длительный процесс, требующий больших затрат, при котором
возможны аварии и остановки производства вследствие поломок оборудования при
проведении экспериментальных работ.
В связи с этим одним из существенных аспектов решения
этой проблемы является необходимость расчётов потребного количества воды для
водоснабжения станов ещё на этапе их проектирования или реконструкции. Подобные
расчёты могут быть произведены только на основе апробированных математических
моделей тепловых процессов, происходящих в системе прокатываемая полоса -
валок.
Таким образом, целью
настоящих исследований теплового баланса системы прокатываемая полоса –
валок является разработка методики проектирования систем водоснабжения
прокатных станов с управлением процессом по критерию экономии энергии.
Поставленная задача может быть решена путём
математического моделирования теплового состояния металла [5] и валков. Из
приведенной в работе [5] математической модели теплового состояния системы
полоса-окалина-валок, охватывающей все участки горячей прокатки листа, где
происходят активные процессы теплообмена:
-
для полосы при ![]() и
и ![]() >0
>0
 (1)
(1)
-
для окалины при H-d<x<0+d; B-d<y<0+d; L-d<z<0+d и ![]() >0
>0
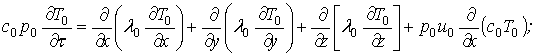 (2)
(2)
-для
валка H<x<0; B<y<0; L<z<0 и ![]() <0
<0
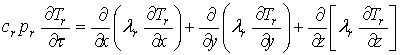 , (3)
, (3)
наибольший
интерес представляет участок деформации полосы в валках (рис.1) и участок
принудительного охлаждения со следующими начальными и граничными условиями:
![]() начальные условия Tm=f(xm, ym, zm);
начальные условия Tm=f(xm, ym, zm);
при t=0
T0=f(x0, y0, z0); (4) Tr=f(xr, yr, zr);
граничные
условия на участке деформации на границе окалина-валок
![]() при х=0
при х=0 ![]()
![]()
при х = Н ![]()
![]()
при y=0 ![]()
![]() (5)
(5)
при y=B ![]()
![]()
при z=0 ![]() -
-![]() -Т0)=0;
-Т0)=0;
при z=L ![]() -
-![]() -Т0)=0;
-Т0)=0;
граничные условия на
участке деформации на границе окалина-полоса
![]() при х=d
при х=d ![]()
![]()
при х=Н-d ![]()
![]()
при y=d ![]()
![]() (6)
(6)
при y=B-d ![]()
![]()
при z=d ![]()
![]()
при y=L-d ![]()
![]()
![]() граничные условия на участке
принудительного охлаждения
граничные условия на участке
принудительного охлаждения
при х=0 ![]() -
-![]() -T0
-T0![]() =0; (7)
=0; (7)
при х=Н ![]() -
-![]() -T0
-T0![]() =0;
=0;
![]() при y=0
при y=0 ![]() -
-![]() -T0
-T0![]() =0; (7)
=0; (7)
при y=B ![]() -
-![]() -T0
-T0![]() =0;
=0;
при z=0 ![]() -
-![]() -T0
-T0![]() =0;
=0;
при z=L ![]() -
-![]() -T0
-T0![]() =0;
=0;
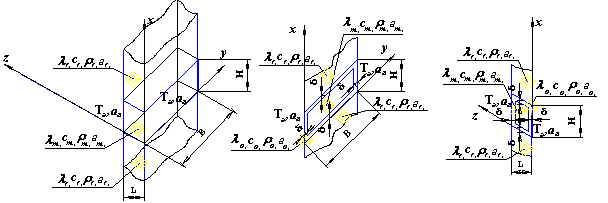
Рис. 1. Схема распределения теплофизических характеристик пластины на
участке деформации (тепловыделение от пластической деформации – qv равномерное по сечению пластины)
В
уравнениях 1-7: Tm, T0, Tr – температура полосы, окалины и
валка соответственно; um =u0+uд – скорость перемещения полосы; u0 – скорость окисления; uд – скорость деформирования; af – коэффициент теплопередачи в
нагревательной печи; aw – коэффициент теплоотдачи на
участке гидросмыва окалины; aa=aconv+aair ; aconv – коэффициент теплоотдачи за
счёт конвекции; aair – коэффициент теплоотдачи в
окружающую среду; ap – коэффициент теплоотдачи в
установках ускоренного охлаждения; Tf – температура печи; Tw – температура воды; Ta – температура окружающей среды; qv – тепловыделение от пластической
деформации полосы.
Известно [6], что стойкость
валка в значительной мере зависит от твердости его поверхности. Чем больше
твердость поверхности валка, тем выше его стойкость. Твердость может быть
обеспечена использованием заэвтектоидной стали с содержимым углерода 1,6 – 1,8
%. При нагрузках, которые имеют место на листовых станах, использование
сплошного валка из заэвтектоидной стали проблематично, потому что существует
риск его поломки. Поэтому при теоретических исследованиях рассмотрена схема современного
двухслойного валка (рис. 2).
Процесс
теплопередачи в цилиндре описывается системой уравнений. Дифференциальные
уравнения с соответствующими начальными и граничными условиями для слоев валка:
‑
внутренний слой
при 0 < r < r2; 0 < φ <2π;
0 < y < L
и
τ > 0
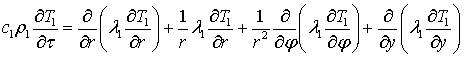 ; (8)
; (8)
‑ бандаж
при r2 < r < R; 0 < φ <2π; L1 < y < L – L5 и
τ > 0
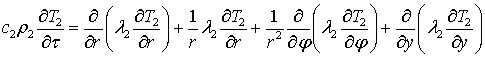 ;
(9)
;
(9)
начальные условия: при ![]()
![]() ; (10)
; (10)
граничные условия: при ![]()
 ; (11)
; (11)
а) б)
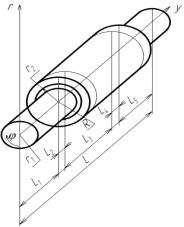
Рис. 2 – Схема
листопрокатного валка:
а) r, у оси координат; r1– радиус опорных шеек; r2 – внутренний
радиус бандажа; R – внешний радиус валка; L длина
валка; L1 длина левой шейки валка; L2 + L3 + L4 – длина
рабочей части валка; L2, L4 – длина
частей бочки валка, не контактирующих с металлом; L3 – ширина
прокатываемой полосы, L5 – длина правой шейки валка
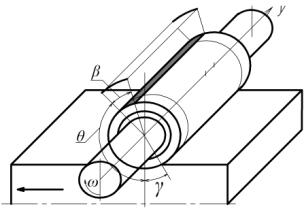
б) g‑
угол ; q‑
угол от выхода полосы из зоны деформации зоны принудительного охлаждения; b‑
угол зоны принудительного охлаждения; ¬ направление прокатки
при ![]()
![]() ; (12)
; (12)
при ![]() ; r1 < r < r2
; r1 < r < r2 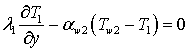 ; (13)
; (13)
при ![]()
![]() ;
; ![]() ; (14)
; (14)
при ![]() ; r2 < r < R
; r2 < r < R 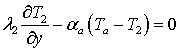 ; (15)
; (15)
при ![]() ;
; ![]()
![]() ; (16)
; (16)
при ![]() ;
; ![]()
![]() (17)
(17)
при ![]() ;
; ![]()
 (18)
(18)
при ![]() ;
; ![]()
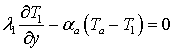 (19)
(19)
при ![]()
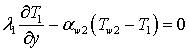 (20)
(20)
при ![]() ;
; ![]()
![]() , (21)
, (21)
где функция
![]() при
при ![]() ;
;
![]() при
при ![]() ;
;
![]() при
при ![]() ;
; ![]() при
при ![]() ;
;
В уравнениях (8–21):
![]() ‑ температура
внутреннего и внешнего слоёв валка, соответственно;
‑ температура
внутреннего и внешнего слоёв валка, соответственно;
![]() ‑ температура
охлаждающей среды в подшипнике;
‑ температура
охлаждающей среды в подшипнике;
![]() ‑ температура
полосы;
‑ температура
полосы;
![]() ‑ температура
води и окружающей среды соответственно.
‑ температура
води и окружающей среды соответственно.
![]() ‑ коэффициент
теплоотдачи в подшипнике;
‑ коэффициент
теплоотдачи в подшипнике;
![]() – коэффициент
теплоотдачи на участке принудительного охлаждения;
– коэффициент
теплоотдачи на участке принудительного охлаждения;
![]()
![]() – коэффициент
теплоотдачи конвекцией;
– коэффициент
теплоотдачи конвекцией;
![]() ‑ коэффициент теплоотдачи в окружающую среду;
‑ коэффициент теплоотдачи в окружающую среду;
![]() ‑ коэффициент теплопередачи от полосы к валку.
‑ коэффициент теплопередачи от полосы к валку.
Теплообменом
с окружающей средой поверхностей, не контактирующих с прокатываемым металлом и
охладителем, пренебрегаем.
Созданные математические модели должны базироваться на
надёжных данных о граничных условиях теплообмена в зонах нагрева и охлаждения
[6] .
Данные по значениям коэффициентов теплоотдачи для
различных устройств подачи воды можно
получить в лабораторных условиях. Естественно, результаты замеров на лабораторных
установках должны быть математически обработаны – необходимо выполнить решение
обратной задачи теплопроводности [7].
Поскольку известно, что ошибка выполнения
теплотехнических измерений существенно зависит от методики их проведения,
немалое значение имеет правильно выбранная методика и аппаратная база
проведения этих исследований. Доказано [8], что в случае применения фольговых
термопар толщиною 10 мкм ошибка
измерительного комплекса (термопара – прибор) значительно меньше ошибки, с
какой в справочной литературе приведены значения теплофизических характеристик полосы. Апробированная в работе
[8]система регистрации температуры позволила выполнить комплекс исследований,
позволяющих уточнить скорость изменения температуры поверхности испытываемых
образцов под воздействием интенсивного
охлаждения водой.
Имея математические модели с надёжными данными про
условия теплообмена, возможно рассчитать тепловое состояние объектов с распределёнными
параметрами на всех участках технологического процесса, определить необходимое
количество воды в системе водоснабжения. На основе этих данных можно сформулировать требования по условиям
подготовки воды и её подачи в систему водоснабжения прокатных станов.
Разработанные математические модели использовали для
анализа эффективности применяемого процесса охлаждения полосы. Установлена
зависимость количества воды в системах водоснабжения от способа её подачи, а
также возможность использования наиболее эффективной системы охлаждения,
которая обеспечивает современный технологический режим прокатки листа в
непрерывном технологическом цикле, что соответствует современному мировому
уровню.
ВЫВОДЫ
На основе теоретического анализа разработаны
математические модели теплового состояния полосы и валков при горячей прокатке
листового материала, позволяющие рассчитать тепловое состояние объектов с
распределёнными параметрами на всех участках технологического процесса.
Полученные модели можно использовать для анализа эффективности применяемого
процесса охлаждения полосы, установления зависимости количества воды в системах
водоснабжения от способа её подачи, а также выбора наиболее эффективной системы
охлаждения. Выполненные исследования могут служить основой для решения задач
создания прокатного оборудования IV поколения, а также реконструкции действующих станов горячей прокатки листа.
БИБЛИОГРАФИЧЕСКИЙ
СПИСОК
1. Hendricks, C. Start-up and initial experience with the
casting-rolling plant of The Krupp Stahl AG [Техt] / C. Hendricks, W. Rasim, H. Janssen //
La Reviu Metallurgie . – CIT, 2001. № 78. – P.633-666.
2.
Деглер М. Новые технические разработки в области горячей прокатки полосы
[Текст] /М. Деглер, У.Тамлер // Чёрные металлы. – 2001. – № 10. – С.15-17.
3. De Paepe, A. Control of the temperature of the bar
on entry to the finisher [Техt]
/ A. De Paepe, P. Simon, I. Moerkerke, C.Herman // ECSC STEEL RTD POGRAMME. –
2000. – P. 1 – 9.
4. Пантелят Г.С. Управление водоснабжением прокатных станов по критерию экономии
энергии [Текст] / Г.С. Пантелят, Н.В. Салтавец // Науковий вісник
будівництва. – Харків: ХДУБА, ХОТВ АБУ, 2003. –
Вип.12. – С.70-73.
5. Салтавець В.І. Розробка математичної моделі теплового стану металу під час прокатки [Текст] / В.І. Салтавець, Н.В. Салтавець // Науковий вісник
будівництва. – Харків: ХДУБА, ХОТВ АБУ, 2003. –
Вип.21. – С.162-169.
6. Saltavets W. Increase
in hot mill roll life [Техt]
/ W. Saltavets, N.Kirjukhin, W.Luke,
W.Liddle // 43 Mechanical Working and Steel Processing Conference. Charlotter,
North Carolina, USA.- Oct. 2001/– P. 437 – 449.
7. Коздоба Л.А. Методы решения обратных задач теплопереноса [Текст] / Л.А. Коздоба, П.Г.Круковский // Киев: Наук.
думка, 1982. – 360 с.
8. Тришевський О.І. Система
реєстрації температури в процесах обробки
металів тиском [Текст] / О.І.
Тришевський , М.В.Салтавець // Удосконалення процесів і обладнання
обробки тиском в металургії і машинобудуванні. – Краматорськ: ДДМА, 2005. – С.107-110.
9.
Матвеев Б.Н. Совершенствование непрерывного производства горячекатаной широкополосной
стали [Текст] / Б.Н. Матвеев – Производство проката. – 2002.– №4.
–С.17-24.