к.т.н. Дорофєєв О.А.

Хмельницький національний університет, Україна

ВИЗНАЧЕННЯ РОЗРАХУНКОВИХ ПАРАМЕТРІВ МОДЕЛЕЙ ДИСКРЕТНОГО СЕРЕДОВИЩА

До класу дискретних матеріалів відносять штучно створені або природні зернисті, гранульовані, сипкі, дисперсні матеріали. Методи механіки дисперсних середовищ використовують також для оцінки напружено-деформованого стану ґрунтів, тріщинуватих гірських порід, композитних матеріалів.

Завдання експериментальних досліджень на початковому етапі розробки моделей механіки дискретного середовища полягає у вивченні принципіальних особливостей поведінки дискретного матеріалу при зовнішніх збуреннях, а після створення теоретичних моделей – у конкретизації характеру визначувальних співвідношень і визначенні їх параметрів.

Особливості поведінки дискретних матеріалів при дії зовнішніх навантажень достатньо вивченні. Вони зводяться до наступних: а) дискретні матеріали не сприймають розтягуючих напружень і не можуть зберігати подібно твердим тілам початкову форму; б) вони опираються деформаціям зсуву тільки при наявності стискуючих нормальних напружень на поверхнях зсуву (прояв внутрішнього сухого кулонового тертя); в) деформації зсувів у дискретному середовищі супроводжуються зміною об’єму (прояв дилатансії); г) закони деформування дискретних матеріалів суттєво залежать від виду напруженого стану.

Вказані особливості здебільшого встановлені для граничного стану і потребують додаткового вивчення в дограничній стадії деформування матеріалу.

Для аналізу напружено-деформованого стану дискретного середовища розроблена велика кількість розрахункових моделей. Першими були запропоновані моделі контактної взаємодії частинок середовища.

В інженерній практиці достатньо розповсюджені бездеформаційні моделі статики сипкого середовища, які розглядають середовище тільки у граничному стані. Єдиною розрахунковою характеристикою цих моделей, значення якої необхідно визначити експериментальним шляхом, є параметр гіпотези Мора-Кулона – кут внутрішнього тертя для випадку плоскої деформації або параметр Боткіна для випадку осесиметричної задачі.

Для оцінки дограничного напружено-деформованого стану сипкого середовища в умовах експлуатації, використовують більш складні деформаційні моделі, що дозволяють описати поведінку середовища в дограничній стадії [1]. Ці моделі розглядають сипке середовище як квазісуцільне з особливими лінійними або нелінійними законами деформування

Лабораторне обладнання та методики, що розроблені для випробувань зразків твердих матеріалів, не можуть бути безпосередньо використані для досліджень дискретних матеріалів. Навантажувальні і вимірювальні системи повинні забезпечити реалізацію характерних для дискретних матеріалів траєкторій навантаження та фіксувати значення усіх компонентів тензорів напружень і деформацій. При цьому необхідно враховувати, що величини напружень в зразках дискретного матеріалу на порядок менші, а деформації, що виникають, – на порядок більші, ніж при випробуваннях зразків твердих матеріалів.

Випробування бажано проводити при тому самому напруженому стані, при якому фактично працює матеріал. Сформульованим вимогам в найбільшій мірі відповідають прилади, розроблені для випробувань ґрунтів: компресійні, зрізні прилади та стабілометри.

Розроблені в ХНУ оригінальні методика [2] та прилад [3] дозволяють усунути ряд недоліків існуючих приладів.

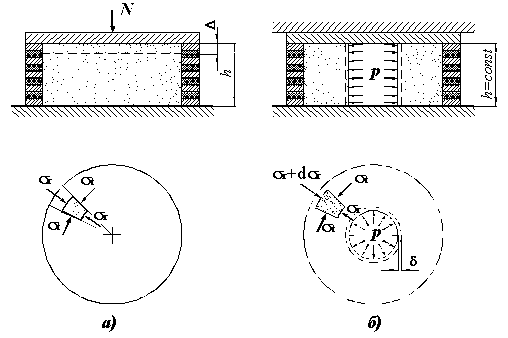
Зразок дискретного матеріалу випробовується в два етапи. На першому етапі (рис. 1, а) здійснюється осьове навантаження зразка в спеціальній обоймі, стінки якої стискуються разом із зразком в осьовому напрямі, але є жорсткими у радіальному напрямі. Це дозволяє визначати величину модуля Е аналогічно стандартним компресійним випробуванням з єдиною відмінністю – сила , що деформує зразок, знаходиться як різниця загальної сили , що передається як на зразок, так і на стінки, та сили , яка стискає тільки стінки обойми – . Деформування зразка разом з обоймою дозволяє уникнути спотворюючого впливу тертя по внутрішній поверхні обойми. На першому етапі випробувань у зразку створюється однорідний напружено-деформований стан –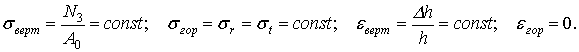

Рис. 1. Етапи випробування зразка в умовах одномірної деформації

В інтервалі лінеаризації кривої "напруження-деформація", використовуючи формули узагальненого закону Гука, одержують зв’язок між модулем Юнга Е та коефіцієнт Пуассона

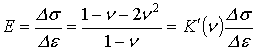. (1)

На другому етапі (рис. 1, б) випробовується зразок у формі товстостінного порожнистого циліндра під впливом внутрішнього тиску р, що передається через еластичну оболонку. Вертикальні переміщення обмежуються нерухомим штампом , а горизонтальні переміщення зовнішньої стінки циліндра – жорсткою у радіальному напрямі обоймою. В процесі випробування фіксуються тиск р і радіальні переміщення d внутрішньої поверхні циліндра. Лінеаризуючи графік та використовуючи відоме рішення Ляме для товстостінних циліндрів, одержують друге співвідношення між параметрами Е і

. (2)

З двох співвідношень (1) і (2) визначають величини двох необхідних для розрахунків параметрів моделі лінійної теорії пружності: модуля Юнга Е і коефіцієнта Пуассона .

Експериментальне забезпечення розрахунків за бездеформаційними моделями в першу чергу зводиться до визначення розрахункових показників дискретного середовища, що описують його граничний стан.

Враховуючи суттєву залежність показників дискретних матеріалів від виду напружено-деформованого стану, для визначення їх величин, а також для вивчення закономірностей деформування в умовах осесиметричного навантаження, використовують більш функціональні прилади тривісного стиснення (стабілометри).

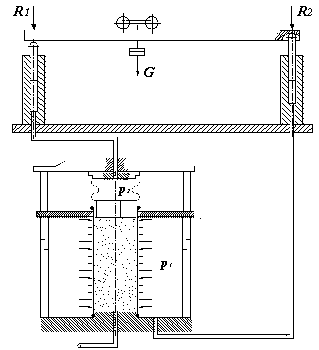
Рис. 2. Принципова схема навантажувальної системи

Для розширення можливостей керування "траєкторією" навантаження зразка розроблений прилад з оригінальною гідравлічною навантажувально - вимірювальною системою і системою створення зразка дискретного матеріалу циліндричної форми [4], [6]. Принципова схема приладу та навантажувальної системи приведена на рис. 2. Система дозволяє проводити випробування зразка при будь-яких відношеннях головних напружень і фіксувати на кожному етапі величини усіх головних напружень , , та відповідних деформацій , , .

Стабілометричні випробування зразків дискретного матеріалу за розробленою методикою дозволяють не тільки визначати параметри граничного стану матеріалу для умов осесиметричного напруженого стану, але й встановлювати відповідність вихідних положень розрахункових моделей фактичним законам деформування дискретних матеріалів.

В стабілометричних випробуваннях створюється тільки частковий випадок осесиметричного напруженого стану, коли два головних напруження однакові за величиною . Для випробувань зразків дискретного матеріалу в умовах довільного тривісного напруженого стану запропоновані прилади з кубічними зразками.

Принципово ці прилади дозволяють реалізовувати будь-які траєкторії навантаження, тобто відтворювати в зразку який завгодно напружений стан. Однак, суттєві технічні труднощі, що виникають при створенні початкової геометричної кубічної форми зразка і фіксації деформацій при його навантаженні, не дозволили впровадити вказані прилади в лабораторні випробування.

Серед безлічі можливих видів напружено-деформативних станів в практиці інженерних розрахунків найчастіше розглядають тільки два види: осесиметричне навантаження, яке моделюється в стабілометричних випробуваннях і плоску деформацію. Хоча плоска деформація в першу чергу цікавила інженерів, приладів, які б відтворювали цей вид напружено-деформативного стану в лабораторних умовах, практично не створено. Розглянемо це питання більш детально.

В приладах плоскої деформації необхідно забезпечити неможливість деформування в одному з напрямків і однорідність напруженого стану в усіх перпендикулярних до цього напрямку перерізах.

Принципові схеми приладів плоскої деформації запропоновані К. Роско, В. Ковтуном, Ф. Шихієвим, В. Алписовою. Оптимальною схемою випробувань зразка дискретного матеріалу в умовах плоскої деформації є передача стискуючих навантажень через еластичні мембрани в поперечній площині за умови неможливості деформування в осьовому напрямі.

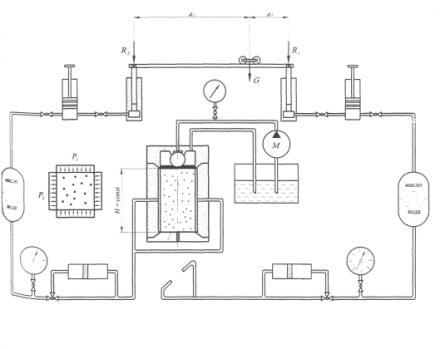
Рис. 3. Схема випробувальної системи

За цією схемою в лабораторії кафедри інженерної механіки ХНУ розроблені прилад [5] і навантажувально-вимірювальна система [6], які дозволяють при випробуванні зразка в умовах плоскої деформації створювати зразок дискретного матеріалу правильної призматичної форми, навантажувати його за будь-якою траєкторією та фіксувати при цьому всі головні напруження і деформації , .

Схема випробувальної системи показана на рис. 3.

Випробовується зразок призматичної форми, який за допомогою спеціальних пристроїв формується безпосередньо в камері приладу. Кришка приладу жорстко з’єднана з боковими стінками, що унеможливлює осьові деформації зразка. На бічні грані зразка через еластичні мембрани передаються тиски і , створені гідравлічною навантажувальною системою, яка дозволяє змінювати їх величини у необхідному співвідношенні. Напруження, що виникають по площинам, паралельним бічним граням, є головними напруженнями , . Третє осьове напруження фіксується спеціальним датчиком, вмонтованим в кришку приладу. Деформації , , викликані переміщеннями бічних граней, визначаються за допомогою волюметрів, які фіксують зміну об’єму води, що поступає в порожнини камери.

Оскільки в процесі випробувань на кожному етапі фіксуються усі компоненти тензора напружень і тензора деформацій, описана випробувальна система дозволяє досліджувати закони деформування дискретних матеріалів в умовах плоскої деформації, обґрунтовувати вихідні положення теоретичних моделей і визначати величини необхідних для конкретних розрахунків показників матеріалу.

За допомогою лабораторних досліджень вивчаються закономірності деформування дискретних матеріалів від початку навантаження до моменту їх переходу у граничний стан. Це необхідно для обґрунтування вихідних положень при формулюванні теоретичних моделей дискретного середовища і для визначення розрахункових параметрів конкретного матеріалу при використанні обраної моделі.

Для дослідження закономірностей деформування і обґрунтування визначувальних співвідношень "напруження-деформації" дискретного матеріалу перш за все необхідно вибрати траєкторію навантаження у просторі напружень, тобто задати послідовність зміни усіх компонентів тензора напружень, щоб досягти необхідного напруженого стану.

В механіці твердого деформівного тіла особливу увагу приділяють прямолінійним траєкторіям навантаження, які відповідають монотонній пропорційній зміні напружень.

Для спрощення вибору найбільш інформативних траєкторій запропоновано описувати процес навантаження у просторі інваріантів тензора напружень. Такими інваріантами при випробуванні на стабілометрах, де моделюється осесиметричний напружений стан, вибрано напруження , та деформації , в октаедричній, однаково нахиленій до головних осей площині.

Для плоскої деформації обрані інваріанти, які включають тільки компоненти тензорів в площині деформування , і мають чіткий фізичний зміст:

– середнє нормальне напруження; (3)

– найбільше дотичне напруження; (4)

– об’ємна деформація; (5)

– максимальна деформація зсуву. (6)

Враховуючи те, що для деформування дискретного матеріалу визначувальним є відношення напружень або , а не їх різниця, що характерно для твердих матеріалів, траєкторія навантаження в дослідах на приладах плоскої деформації описувалась особливими інваріантами:

– сума нормальних стискуючих напружень; (7)

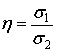– відношення напружень. (8)

Для досягнення граничного стану зразок дискретного матеріалу навантажується за траєкторією, коли сума нормальних напружень впродовж одного досліду залишалась сталою , а їх відношення зростає до настання граничного стану . При дослідженнях закономірностей зміну об'єму створювались траєкторії навантаження, для яких характерно збереження сталою величини відношення напружень і зміна суми нормальних напружень р. Саме такі траєкторії дозволяє відтворювати система навантаження [6].

На описаних вище приладах в умовах осесиметричного навантаження і плоскої деформації випробовувались зразки чистого сухого кварцового піску різної початкової щільності за траєкторіями навантаження: , (стабілометричні випробування); , (плоска деформація).

Визначувальні залежності "напруження-деформації" піску описуються сімействами кривих при або , при , а не "єдиною" кривою або , що характерно для твердих матеріалів. Зростання опору деформаціям зсуву при збільшенні величини стискуючого нормального напруження трактується як прояв внутрішнього кулонового тертя на усіх етапах деформування дискретного матеріалу від початку навантаження до його переходу у граничний стан.

Одержані "безрозмірні" криві можуть бути використані при розробці моделей дискретного середовища, якщо апроксимувати їх простими, зручними для використання функціями. Сімейство експериментальних кривих для осесиметричного напруженого стану задовільно апроксимується степеневою функцією

. (9)

Параметри А і визначались шляхом побудови експериментальної кривої в логарифмічних координатах, де вона представляється прямою .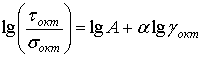

Криві для плоскої деформації більш повно описуються відомою дробово-лінійною функцією

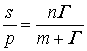. (10)

Для визначення параметрів і експериментальні графіки будувались в "обернених" координатах – ; , – в яких співвідношення (10) перетворюється у лінійне .

За результатами описаних експериментальних досліджень на стабілометрі та приладі плоскої деформації без додаткових випробувань визначаються характеристики граничного стану або , які розглядаються також як параметри сучасних дилатансійних моделей пластичного плину.

Описані в статті методики і створене для їх реалізації лабораторне устаткування дозволяють обґрунтувати вихідні положення теоретичних моделей дискретних середовищ та визначати параметри як відомих, так і нових моделей, без чого вони практично не можуть бути реалізовані.

Література

1. Визначальні співвідношення механіки сипкого середовища / В.В. Ковтун // Вісник ХНУ. – 2008. – №5. Технічні науки. – С. 69-75.

2. Пат. 11675 Україна, МПК (2006) G 01 N 33/24. Спосіб визначення деформаційних параметрів пористих матеріалів за результатами лабораторних випробувань / заявники Ковтун В.В., Багрій О.В.; опубл. 16.01.06, Бюл. №1.

3. Пат. 18390 Україна, МПК (2006) G 01 N 33/24. Пристрій для лабораторних випробувань пористих матеріалів / заявники Ковтун В.В., Багрій О.В.; опубл. 15.11.06, Бюл. №11.

4. Прибор для испытания сыпучих материалов / В.В. Ковтун, О.А. Дорофєєв: праці 3-й Укр. Науч.-техн. конф. ["Механіка грунтів і фундаментобудування"], 17-19 верес. 1997 р., Одеса, Т. 2) / Держкоммістобудування [та ін.], Одес. держ. акад. будівництва і архітектури. – Одеса.: ОДАБА, 1997. – С. 294-295.

5. А.С. 1158925 СССР, Прибор для исследования свойств грунта в условиях плоской деформации / В.В. Ковтун, В.Г. Безносюк, М.А. Мазур (СССР). – опубл. в Б.И. , 1985, №20.

6. А.С. 1141158 СССР, Нагрузочное устройство для испытаний грунтов в приборах трехосного сжатия / В.В. Ковтун (СССР). – опубл. в Б.И. , 1985, №7.