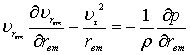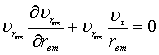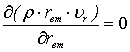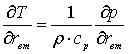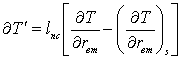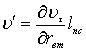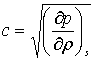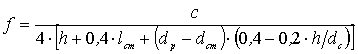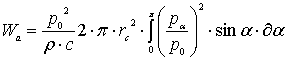Технические науки / 2. Механика

асп. Филатов Д.А.

Иркутский государственный университет путей сообщения, Россия

МОДЕЛЬ ДИНАМИЧЕСКИХ ПРОЦЕССОВ В СИСТЕМЕ УЛЬТРАЗВУКОВОЙ ОЧИСТКИ ТЕХНОЛОГИЧЕСКИХ СРЕД С ПРИМЕНЕНИЕМ ВИХРЕВОГО ЭФФЕКТА

В настоящее время на сети железных дорог Российской Федерации используется пневматическая двухпрограммная автоматическая очистка стрелочных переводов от снега [1]. Очистка производится обдувкой межрельсового пространства сжатым воздухом, подаваемым по специальной пневмомагистрали. Для наиболее эффективной очистки стрелок целесообразно модернизировать существующую пневмоочистку использованием вихревого эффекта (вихревой трубы) и ультразвука (ультразвуковой сирены) для наиболее эффективного дробления и топления снега и льда.

Система будет работать следующим образом: сжатый воздух поступает в вихревую камеру с пневмомагистрали. В вихревой камере сжатый воздух делится на два потока (горячий и холодный). Холодный поток сжатого воздуха выходит через холодный выход вихревой трубы в окружающую среду. Часть горячего сжатого воздуха поступает в ультразвуковую сирену, а другая его часть – в пневмообдувку. После прохождения через ультразвуковую сирену отработанный сжатый воздух на 99% возвращается в пневмообдувку, а сгенерированные им ультразвуковые волны в сирене, наряду со сжатым горячим воздухом пневмообдувки поступают на стрелочный перевод.

Согласно математическим моделям, приведенным в работах [2, 3] математическая модель динамических процессов, протекающих в системе ультразвуковой очистки железнодорожных стрелок с применением вихревого эффекта, состоит из следующей системы уравнений (Таблица 1):

Таблица 1

Название	Уравнение
Уравнения движения
Уравнение сплошности
Уравнение энергии
Уравнение состояния
Уравнение пульсации температуры
Уравнение пульсации скорости при изотропной турбулентности
Уравнение местной скорости звука
Уравнение длины волны пространственной осцилляции струи
Уравнение частоты генерации излучателя
Уравнение интенсивности звука	P
Уравнение акустической мощности

Здесь:

– радиальная скорость;

– тангенциальная скорость;

– радиус вихревой трубы;

– плотность;

p – статическое давление;

T – статическая температура;

– изобарная теплоемкость;

g – ускорение силы тяжести;

R – газовая постоянная;

– длина пути смещения (из теории Прандтля);

h – глубина резонатора;

– длина стержня;

– диаметр резонатора;

– диаметр стержня;

– диаметр сопла;

s – индекс, указывающий на изоэнтропичность процесса;

– коэффициент, изменяющийся для разных типов сопел в пределах от 0,77 до 1,22;

– среднее значение, принятое Эмденом;

– амплитуда колебательной скорости;

– амплитуда смещения;

P – радиационное давление;

– эффективное значение звукового давления на расстоянии ;

– угол сдвига фаз.

Согласно математической модели все основные зависимости выводятся из формулы [2, 4]:

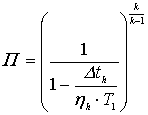, (1)

где – располагаемая степень расширения сжатого воздуха, при ;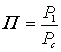

– потребный эффект нагревания, при ;

– температурная эффективность горячего потока, при = 4.305;

– температура сжатого воздуха на выходе из пневмомагистрали, при = 289 К;

– температура горячего сжатого воздуха на горячем выходе из вихревой трубы, при = 350 К;

– показатель адиабаты, при = 1.4 (для воздуха).

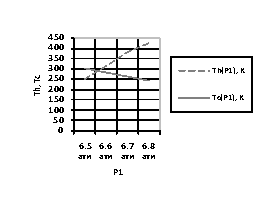
Рисунок 1.

Согласно рисунку 1 видно, что, управляя параметром давления входного потока воздуха, мы управляем изменением параметра температуры на холодном и горячем выходах вихревой трубы до тех пор, пока не будет достигнута рабочая температура = 350 К.

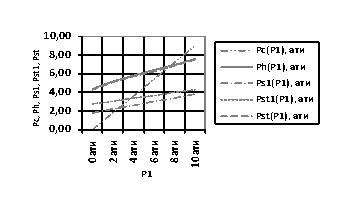
Рисунок 2.

Согласно рисунку 2 видно, что, при управлении параметром давления входного потока воздуха, изменяются параметры давления сжатого воздуха , , , , – соответственно на горячем и холодном выходах из вихревой трубы, на входе в ультразвуковую сирену, на входе и выходе из пневмообдувки, до тех пор, пока не будет достигнуто рабочее давление = 7 ати.

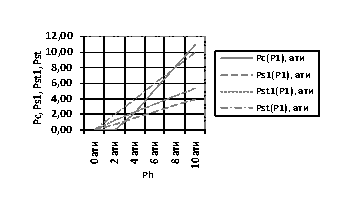
Рисунок 3.

Согласно рисунку 3 видно, что, при управлении параметром давления горячего сжатого воздуха на выходе из вихревой трубы, изменяются параметры давления сжатого воздуха , , , – соответственно на холодном выходе из вихревой трубы, на входе в ультразвуковую сирену, на входе и выходе из пневмообдувки до тех пор, пока не будет достигнуто рабочее давление = 3 ати.

Системный анализ процессов движения воздушной среды в вихревой камере позволяет определить оптимальные параметры сирены, вихревой трубы и определить способ управления ультразвуковой системой очистки [5, 6].

Литература:

1. Берещанский А.Н. Автоматическая пневмоочистка стрелок. Напольное оборудование и воздухопроводная сеть. Типовые материалы для проэктирования: ОАО “РОСЖЕЛДОРПРОЕКТ”. – М. 2006. – 1-29 с.

2. Меркулов А.П. Вихревой эффект и его применение в технике. Издательство “Машиностроение”. – М., 1969. – 7-64 с.

3. Розенберг Л.Д. Источники мощного ультразвука. Физика и техника мощного ультразвука: издательство “НАУКА”. – М., 1967. – 11-106 с.

4. Филатов Д.А. Математическое описание процессов в системе ультразвуковой очистки железнодорожных стрелок с применением вихревого эффекта // Системы. Методы. Технологии. – 2012. – №4(16). – С. 82-86.

5. Мухопад Ю.Ф. Микроэлектронные системы управления. – Братск: БрГУ, 2009. – 285с.

6. Филатов Д.А., Мухопад Ю.Ф. Методика контроля и управления турбо-механизмами // Современные технологии. Системный анализ. Моделирование. – 2012. – №4(36). – С. 117-125.