Бондаренко
Л. Н., Бондаренко В. Д., Матвиец Т. В., Герасимова К. Д.,
Лозовая В. В.
Соотношения между сопротивлением
вращению и диаметром опорно-поворотных устройств (ОПУ) кранов
Приднепровская
государственная академия строительства и архитектуры
ОПУ кранов с опорно-поворотным кругом
(шариковые, роликовые) воспринимают вертикальные и горизонтальные нагрузки, не
требуют центрирующих и удерживающих устройств, компактны, надежны и долговечны,
поэтому в настоящее время получают наибольшее распространение по сравнению с
ОПУ с неподвижной или вращающейся колоннами.
Если для
определения допускаемых нагрузок на ОПУ имеются графики, то для определения
сопротивления вращению применяются приведенный коэффициент сопротивления
вращению (ω=0,01 для шариковых кругов и ω=0,012 для роликовых).
Величины ω
получены экспериментально и для более точного знания их
величины необходимо иметь аналитические зависимости, которые бы удерживали
общепринятые механические константы и размеры.
Если
нагрузка на группу шариков (роликов) изменяется от ноля до допустимой величины
примерно по линейному закону, то при определении сопротивления качению группы
всю нагрузку можно сосредоточить на один шарик (ролик) [1].
Для ОПУ
распределим реакции момента М от груза на два диаметрально расположенных шарика
(ролика).
Момент М
будем считать постоянным, а диаметр круга изменять в реальных пределах. Радиус
дорожки катания для шарикового ОПУ примем равным rд=0,515dш
(рис
1.).
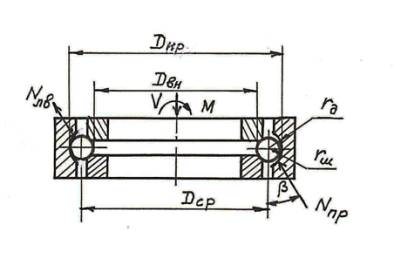
Рис.1
Расчетная схема шарикового поворотного круга
Поскольку
реакция, воспринимаемая левым и правым шариком равна N=M/D,
то исходя их теории контактных напряжений Герца можно найти радиус условного
шарика в зависимости от D. В случае равенства
модулей упругости при вдавливании для материалов шарика и беговой дорожки, а
также при равенстве коэффициента Пуассона 0,3 [2]
(1)
где np
– коэффициент, зависящий от соотношений коэффициентов уравнения эллипса
касания; σ – допускаемые контактные напряжения при первоначальном точечном
контакте; Е – модуль упругости материалов шарика и беговой дорожки; β
– угол наклона реакции.
Полуширина
пятна контакта в направлении движения шарика
 (2)
(2)
где nв – коэффициент,
зависящий от тех же параметров, что и np. Отметим, что при rд=0,515dш
А/В=0,029 и np=0,63, а nв=0,41.
В [3]
доказано, что коэффициент трения качения может быть найдет аналитически через
величину b и первоначальном точечном контакте.
 (3)
(3)
Сопротивление вращению
ОПУ с учетом двух противоположных шариков
 (4)
(4)
а момент, необходимый
для поворота ОПУ
 (5)
(5)
Для
роликового ОПУ при допущении, что диаметр ролика dp равен его длине В,
получим соответствующие вышеприведенным формулам
 (6)
(6)
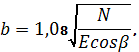 (7)
(7)
 (8)
(8)
(9)
 (10)
(10)
Зависимости
радиусов шарика и ролика от диаметра круга при М=700кНм; σ=1400МПа для шариков и σ=980МПа
для роликов; Е=2,1.105МПа показаны на рис. 2а, а
сопротивление повороту – на рис. 2б.
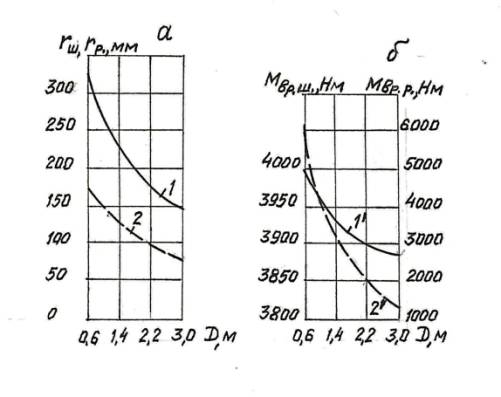
Рис. 2
Зависимости от диаметра круга ОПУ: 1,2 – радиуса условного расчетного шарика и
ролика (а); 1’,2’ – момента на преодоление сопротивлений качению шариков и
роликов.
Анализ
формул (4), (9), (5), (10) и графиков на рис. 2а и 2б позволяют сделать
следующие выводы:
- Расчетный радиус
шариков и роликов немного уменьшается с увеличением диаметра круга и при D=0,6м
и D=3м его величина отличается более, чем в 2 раза как для
шариков, так и для роликов; - момент на преодоление
сил трения качению как для шарикового, так и для роликового ОПУ нелинейно
уменьшается с увеличением диаметра круга и разница в величинах достигает 3% для
шарикового ОПУ и 8% для роликового.
ЛИТЕРАТУРА
1. Бондаренко Л.М., Ракша
С.В., Брильова М.Г. Уточнення розрахункової схеми
навантаження групи тіл кочення / Підйомно-транспортна техніка.
–ДІІТ-№1.-2005.-с.47-52.
2. Справочник по
сопротивлению материалов / Писаренко Г.С., Яковлев А.П., Матвеев В.В. – Киев:
Наук. думка. 1988.-736 с.
3. Бондаренко Л.М. Аналітичні залежності для визначення коефіцієнта тертя коченню для найбільш важливих схем дотику / Техніка будівництва. - №11. – 2002. – с.32-35.