Ю. В. Ващёнок, А. С. Бобылёв, Ю. А. Гурвич

Белорусский национальный технический университет

Определение устойчивости маятника методами Ляпунова

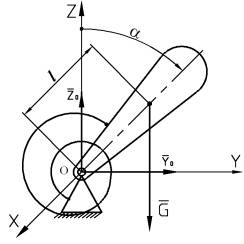
Положение равновесия физического маятника, в котором его центр масс находится над опорой неустойчиво. Для стабилизации этого положения между телом и опорой помещена спиральная пружина, создающая восстанавливающий момент М, пропорциональный углу наклона маятника α и равный М = сα, где с - жесткость пружины. Выполним анализ устойчивости маятника методами А.М. Ляпунова.

В соответствии с теоремой первого метода Ляпунова если , то этот знак положительный и корни характеристического полинома чисто мнимые этот случай относится к критическому, т.к. вещественная часть корней равняется нулю (Re λ₁ = Re λ₂ = 0). Этот случай должен быть исследован дополнительно вторым методом Ляпунова.

Второй метод Ляпунова. Рассмотрим подробнее критический случай. Для этого необходимо ввести функцию Ляпунова , которая должна обладать рядом свойств, описанных в литературе [1-3].

В качестве функции Ляпунова предлагаем ввести определенно-положительную квадратичную форму, которую получим разложением в ряд полной энергии при условии, что . Тогда функция Ляпунова приобретает вид:

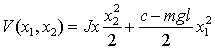. (1)

Функция (1) отвечает всем условиям функции Ляпунова: является вещественной, однозначной, непрерывной, знакоопределенной функцией, обращается в нуль при , при .

Возьмем полную производную по времени от функции Ляпунова

. (2)

Будем считать, что отклонения маятника от вертикального положения невелики. Тогда в качестве уравнений возмущенного движения используем уравнения первого приближения:, . Теперь подставим в выражение полной производной по времени от функции Ляпунова (2) значения . В итоге получим выражение тождественно равное нулю

.

Если производная по времени от функции Ляпунова тождественно равна нулю , то согласно теореме об устойчивости по второму методу Ляпунова состояние равновесия маятника при его вертикальном положении - устойчиво. Система подпружиненного физического маятника имеет единственное состояние равновесия при α=0 (вертикальное положение маятника) в случае , что доказано с помощью второго метода Ляпунова.

Третий метод Ляпунова. Если в положении абсолютного равновесия потенциальная энергия не имеет минимума и его отсутствие определяется членами второго порядка малости без необходимости рассмотрения членов более высокого порядка, то равновесие неустойчиво. Теорема Ляпунова справедлива и для относительного равновесия, если уравнение

= Q + - (s=1,…, n)

Не содержит обобщенных потенциальных и гироскопических сил. Корни x_1 … x_2 векового уравнения:

= 0

Где = =

И производные вычисляются для положения равновесия, называются коэффициентами устойчивости, а число отрицательных корней – степенью неустойчивости. Положение равновесия физического маятника, в котором его центр масс находится над опорой, неустойчиво. Для стабилизации этого положения между телом и опорой помещена спиральная пружина, создающая восстанавливающий момент, пропорциональный углу a наклона маятника. Каким следует выбрать коэффициент пропорциональности, чтобы желаемая стабилизация была достигнута. Потенциальная энергия сил, действующих на тело, имеет вид П (a) = mgl cos a + с

Z—расстояние между осью качания маятника O и его центром тяжести G, с —
искомая жёсткость пружины. B положении равновесия П' = —mgl sin a + ca = 0. При любых значениях параметров уравнение равновесия имеет решение a = 0. Отвечающее этому решению положение равновесия устойчиво, если П " (0) = —mgl + с > 0.