Определения
длины совершенного гидравлического прыжка по данным лабораторных исследований
С.К. Джолдасов,
Г.А. Сарбасова, С.Т. Дуйсенбаева., А. Амангельдиева, М.Н. Сарбас
Таразский государственный университет им. М.Х. Дулати, г.Тараз, Казахстан
Общие сведения
Анализ основного уравнения плавно изменяющегося
неравномерного движения жидкости
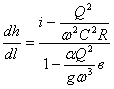или
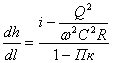(1)
показывает,
что при 
в = 1, (h = hкр
или Пк = 1), 
∞.
Это явление получается всякий раз,
когда в силу каких-либо причин происходит изменение глубин потока, от глубин
меньших критических до глубин больших критических. Это явление, характеризуемое
резким изменением глубин потока на коротком расстоянии и, следовательно, резким
изменением скорости движения, называется гидравлическим прыжком.
Прыжок есть промежуточная, устойчивая по времени,
форма движения, возникающая при
переходе бурного потока в спокойный. С гидравлическим прыжком
встречаемся при работе почти всякого гидротехнического сооружения.
Структура гидравлического прыжка
показывает, что в нем ясно выделяются две зоны: зоны поступательного движения в
форме растекающейся струи и поверхностная зона в виде вращающегося вальца,
насыщенного воздухом. Размеры зон прыжка и формы движения в них зависят от
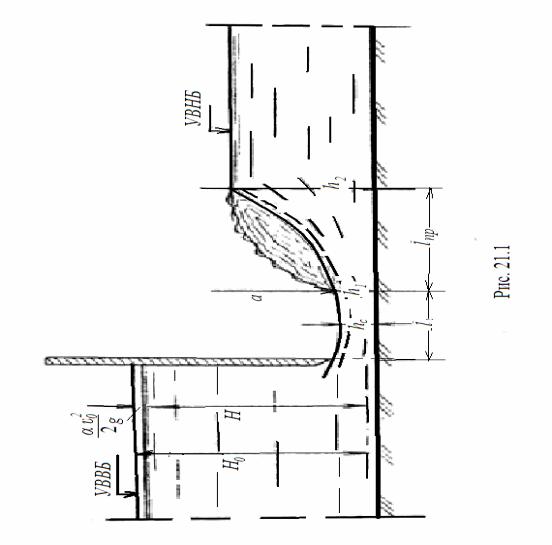
размеров самого прыжка, формы русла, его уклона. Размеры прыжка (рис. 1)
характеризуется высотой прыжка a, равной разности глубин в начальном и конечном
сечениях прыжка aпр=h2 - h1 и
длиной прыжка l np.
Глубина прыжка h1 – начальная
глубина или глубина в сечении перед прыжком, h2 – конечная глубина в сечении за прыжком. Длина прыжка
l np – это расстояние между
начальным и конечным сечениями
гидравлического прыжка. За начальное сечение гидравлического прыжка принимается
такое сечение в бурном потоке перед
прыжком, в котором еще сохраняется эпюра скоростей, присущая плавно
изменяющемся движению. За конечное сечение прыжка принимается такое сечение, в
спокойном потоке за прыжком, в котором плавно растекающийся поток имеет эпюру
скоростей в дальнейшем мало изменяющуюся. Начальная и конечная глубина прыжка
взаимно связаны между собой и носят название взаимных сопряженных глубин. В
гидротехнической практике встречаются следующие виды гидравлических прыжков:
совершенный прыжок, прыжок – волна, подпертый, подтопленный и поверхностный.
Различные виды прыжков зависят от типов гидротехнических сооружений и условий
протекания потока по сооружению.
Для совершенного гидравлического прыжка
в призматическом русле при уклоне дна i=0, применяя закон количества движения к отсеку жидкости, заключенному между начальным и
конечным сечениями прыжка получаем, уравнение сопряженных глубин (уравнение
Беланже- Буссинеска)
(2)
Анализ показывает, что
величины, находящиеся в левой и в правой половине уравнения, зависят от
соответствующей глубины, т.е.
. (3)
Это выражение называется
прыжковой функцией и обозначается П (h). Тогда (2)
имеет вид П(h1) = П (h2).
Основное
уравнение прыжка и график прыжковой функции
служат для отыскания в прыжке при сложных формах поперечного сечения
русел. Для прямоугольного русла основное уравнение прыжка превращается в
.
(4)
Решая
уравнение (21.4), получаем выражения для вычисления сопряженных глубин
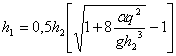
и
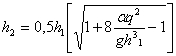. (5)
Длина гидравлического прыжка определяется только опытным
путем и для ее вычисления служат многочисленные эмпирические зависимости.
Наблюдение
процесса образования гидравлического прыжка, установление
параметров гидравлического прыжка
опытным путем, сравнение полученных
параметров с вычисленными по формулам.
Установка для производства опыта,
мерные иглы, масштабная линейка, секундомер и мерный бак.
Опытная
установка (рис.2) состоит из лотка 1 со стеклянными стенками, концевого
затвора 2, промежуточного затвора 3, питающего трубопровода 4 с регулировочным
краном Кр. Отработанная вода из
приемного бака 5, по трубопроводу 6 поступает в мерный бак 7. Экспериментальная
установка находится в лаборатории гидравлики Таразском государственном
университете.
Порядок
выполнения работы
1.
Лоток устанавливается горизонтально.
2. Затвор 3
поднимается над дном на высоту, а=0,3 
0,4 см.
3. Открывая кран Кр. в лоток пускают такой расход,
чтобы уровень воды в верхнем бьефе был ниже верха лотка на 3.0
4,0 см. Пропускаемый расход измеряется объемным способом.
4. Измеряется ширина лотка в в створе затвора 3, мерной иглой измеряется отметка дна перед
затвором 
дна и отметка уровня
воды 
УВ.
5. Медленно поднимая концевой затвор 2, наблюдают
возникновение гидравлического прыжка. Затвор 2
следует поднять на такую высоту, чтобы гидравлический прыжок
располагался ниже затвора 3 на 50 
60 см.
6. Мерной иглой в сечениях 1 и 2 измеряют отметки дна
и уровня воды. Масштабной линейкой измеряет расстояние l и
расстояние lnp между сечениями 1 и 2. При измерении расстояний l и lnp,
а также отметок уровней воды в сечениях прыжка 1 и 2 следует помнить, что все
явления прыжка носят бурный характер, причем прыжок не находится на одном
месте, он совершает некоторые небольшие поступательные движения то вправо, то
влево.
Рисунок 2 – Экспериментальная установка
7. При неизменном расходе Q и неизменном поднятии концевого затвора 2 производят
еще два измерения всех величин для новых открытий затвора 3. В каждом
последующем опыте величина открытия затвора а
увеличивается на 0,2 см.
Длина прыжка является одним из
основных геометрических элементов совершенного гидравлического прыжка. Длина
прыжка обычно определяется по эмпирическим формулам [1-4] и не имеет
даже приближенного теоретического решения. Сопоставление этих формул
показывают, что вычисленные по ним значения длины прыжка дает большое
расхождение. Последнее время получил практическое применение научно
обоснованная зависимость А.А. Абдураманова [5] . На основе лабораторных
исследований имея опытные данные глубин (h1,h2 – первая
и вторая сопряженные глубины) произведем сравнительную оценку, определив длину прыжка
по нижеприведенным формулам.
По формуле Н.Н. Павловского [1] определяем длину прыжка:
при h1 =0,88 см; h2=5,30 см.
при h1 =0,6 см; h2=3,8 см.
при h1 =1,3 см; h2=2,3 см.
По формуле
В.А. Шаумяна [2]:
при h1 =0,88 см; h2=5,30 см.
при h1 =0,6 см; h2=3,8 см.
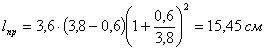
при h1 =1,3 см; h2=2,3 см.
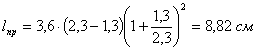
По формуле Сафранца []:
при h1 =0,88 см; h2=5,30 см.
при h1 =0,6 см; h2=3,8 см.
при h1 =1,3 см; h2=2,3 см.
По формуле Б.А. Бахметьева – Матцке []:
при h1 =0,88 см; h2=5,30 см.
при h1 =0,6 см; h2=3,8 см.
при h1 =1,3 см; h2=2,3 см.
По
формуле А.А. Абдураманова [5]:
при h1 =0,88 см; h2=5,30 см.
где 
; 
;
; 
; 
;
; 
.
см.
см.
см2.
см2.
см2.
.
При
h1 =0,6 см; h2=3,8 см.
см.
см2.
см2.
см2.
.
.
При
h1 =1,3 см; h2=2,3 см.
см.
см.
см.
см.
.
По полученным данным строим
график зависимости 
По графику зависимости 
видим большой разброс
точек, что говорить о расхождения результатов вычисления и измеренных опытным
путем в лабораторных условиях.
Для наглядности расчеты приводим в табличной форме и
сравним расчетные данные длины прыжка по формулам Н.Н. Павловского, В.А.
Шаумяна, Сафранца, Б.А. Бахметьева – Матцке, и А.А. Абдураманова с их опытными значениями.
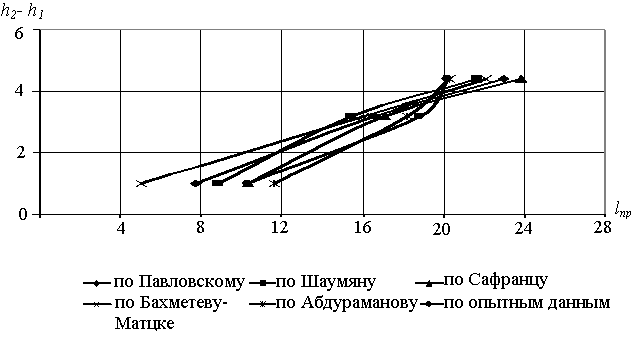
Рисунок 3 – График
зависимости 
Таблица 1 – Сравнение расчетных длин прыжка с их опытными значениями
|
h1, см |
h2, см |
Длина прыжка по формулам |
Измеренная длина прыжка (по лабораторным данным) |
|||||||||
|
по Павловскому |
отклонение от измеренного, % |
по Шаумяну |
отклонение от измеренного, % |
по Сафранцу |
отклонение от измеренного, % |
по Бахметеву-Матцке |
отклонение от измеренного, % |
по Абдураманову |
отклонение от измеренного, % |
|||
|
0,88 |
5,3 |
22,97 |
13,7 |
21,64 |
7,1 |
23,85 |
18,1 |
22,10 |
9,4 |
20,29 |
0,5 |
20,20 |
|
0,60 |
3,8 |
16,55 |
-12,0 |
15,45 |
-17,8 |
17,10 |
-9,1 |
16,00 |
-14,9 |
18,20 |
-3,2 |
18,80 |
|
1,30 |
2,3 |
7,68 |
-25,4 |
8,82 |
-14,4 |
10,35 |
0,5 |
5,00 |
-51,4 |
11,60 |
12,6 |
10,30 |
Из таблицы результатов можно заметить, что самые
близкие измеренные и подсчитанные значения длины прыжка мы получили из
формулы А.А. Абдураманова, В.А. Шаумяна,
Сафранца. Максимальное отклонение от измеренного значения составило
соответственно 12,6%, 17,8%, 18,1%. Проведенный сопоставительный расчет не
может дать заключения по выбору формулы для определения длины прыжка. Для
решения данного вопроса необходимо проведения экспериментальных опытов на
модели и в натуре. Однако, необходимо отметить в отличие от других авторов
(эмпирические формулы) научно обоснованность формулы А.А. Абдураманова, который
получает данную зависимость на основании
теоретических выводов, что позволяет успешно решать практические задачи по
определению геометрических параметров элементов нижнего бьефа гидротехнических
сооружений.
Литература
1. Павловский Н.Н.
Гидравлический справочник, Л-М., Гл.редакция энерг. л-ры, 1937, 890с.
2. Шаумян В.А.
Научные основы орошения и оросительных сооружений. -М.: ОГИЗ - Сельхозгиз,
1948. - 758 с.
3. Справочник по
гидравлическим расчетам /П.Г.Киселев, А.Д.Альтшуль и др. 4е- изд. –
М., Энергия., 1972, 312с.
4. Чертоусов М.Д.
Гидравлика. Специальный курс - 4е- изд. – М.-Л., Госэнергоиздат.,
1962, 630с.
5. Әбдіраманов
Ә. Гидравлика. - Тараз.: Сенім., 2010. – 497 б.