Путят В.А., Иванов М.В., Гурвич Ю.А.

Белорусский национальный технический университет

Приведение систем дифференциальных уравнений движения управляемых колес к форме Коши

Задачу об устойчивости движения управляемых колес сводится к изучению

решения системы дифференциальных уравнений:

(1)

Для приведения системы уравнений (1) к форме Коши введем обозначения:

(2)

Коэффициенты системы уравнений (1) обозначим через в соответствии с таблицей 1:

Таблица 1

Значения коэффициентов k_ij

j	1	2	3	4	5	6	7	8
i
1	- γ0η1	0	η	c1 + η1	- c0v	h1	- γ0J	J1
2	c2	-2b	- γ0η	- γ0η1	h2	c0v	J2	- γ0J
3	v	v	0	0	γ0r	- r	1
4	-γ0γ v	β v	-α v	γ v	1	0	1

Учитывая (2) и обозначения из таблицы 1, получаем систему уравнений

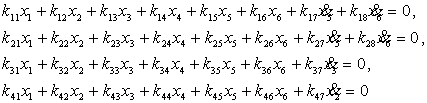(3)

Из первого уравнения системы (3) получаем:

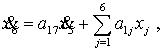(4)

где коэффициенты вычисляются из соотношений:

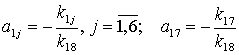. (5)

Из второго уравнения системы (3) получаем:

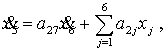(6)

где коэффициенты вычисляются из соотношений:

. (7)

Из (4) и (6) получаем:

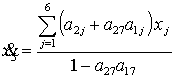. (8)

Обозначим

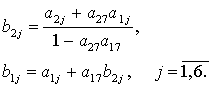(9)

Окончательно получаем систему уравнений (3) в форме Коши:

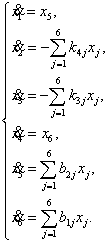(10)