М. В. Иванов, Д.М. Лаптанович, Ю. А. Гурвич

Белорусский национальный технический университет

Механико-математическая модель движения управляемых осей автобусов и автомобилей с учётом характеристик шин

Система дифференциальных уравнений, описывающая малые колебания управляемой передней оси с элементами рулевого привода и подвески автобуса, колеса которого имеют две основные степени свободы – θ и ψ, как известно, имеет вид (отметим, что все параметры шин, входящие в дифференциальные уравнения движения, выделены жирным шрифтом):

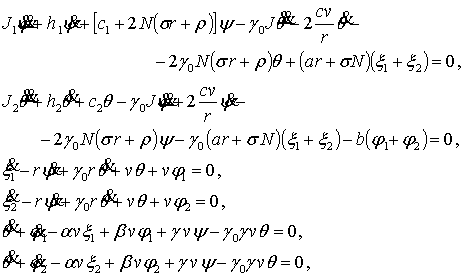(1.1)

где

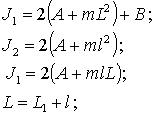
m – масса колеса со ступицей;

L₁ – расстояние от центра масс подвески до центра шкворня;

A – момент инерции колеса со ступицей относительно его диаметра;

C - осевой момент инерции колеса;

B - центральный момент инерции передней оси;

r - радиус качения колеса; угловая скорость собственного вращения колеса ;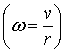

v – линейная скорость центра колеса (или линейная скорость поступательного движения автобуса);

γ₀ – продольный угол наклона шкворня;

2N – нагрузка на переднюю подвеску;

ψ - угол поворота балки передней оси вместе с колесами относительно продольной оси автобуса;

θ – угол поворота колес относительно шкворней;

ξ₁ – боковая деформация левого пневматика;

ξ₂ - боковая деформация правого пневматика;

φ₁ - деформация скручивания левого пневматика;

φ₂ - деформация скручивания правого пневматика;

a – коэффициент боковой жесткости шины;

b – коэффициент угловой жесткости шины;

σ – – коэффициент упругости шины;

ρ – удельная угловая жесткость шины;

α, β, γ – кинематические параметры пневматика;

h₁– коэффициент демпфирования (вязкого трения) в подвеске;

h₂- коэффициент демпфирования в рулевом управлении;

c₁– коэффициент жесткости шин и рессор подвески;

c₂ - коэффициент жесткости рулевого управления.

Уменьшение порядка системы дифференциальных уравнений движения управляемой оси автобуса

Для этого введём вспомогательные параметры:

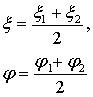
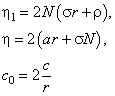
В соответствии с этими обозначениями система дифференциальных уравнений приобретает вид, который был использован для моделирования с помощью персонального компьютера:

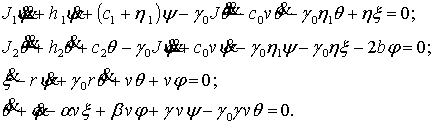(1)

Как и ожидалось, преобразование системы (1) к (2), не нарушает поведения фазовых переменных. Преимущество моделирования по системе (2) состоит в уменьшении влияния погрешностей начальных данных и вычислений за счет уменьшения количества арифметических операций и числа фазовых переменных.