Сигида Ю.Л.
Донской Государственный
Технический университет, Россия
Статистическая обработка данных
наблюдений для задач планирования эксперимента
При решении задач внешней аэродинамики
необходимо четко определить как допустимые диапазоны, так и характерные
значения тех атмосферных параметров, в среде которых будут испытываться объекты
исследований. В частности, при испытании летательных аппаратов (ЛА) интерес
представляют такие параметры как давление, температура окружающего
пространства, скорость и направление ветра. Они необходимы при задании условий
компьютерного имитационного исследования поведения конструкции ЛА в среде плавания. В связи с этим
возникает задача разработки плана достоверного компьютерного исследования
(плана эксперимента), который должен содержать минимальное количество опытов,
проводимых для наиболее характерных сочетаний этих параметров.
Данная работа направлена на выработку наиболее
рациональной методики исследования характеристик среды, систематизации их
описания и рациональной количественной оценке. Атмосферные параметры зависят от
географического положения ЛА и временных характеристик (время суток, погодные
условия времени года и т.д.). Поэтому стандартными исходными данными для
анализа и предполагаемых характеристик воздушных потоков, с которыми ЛА
придется сталкиваться, являются метеоданные. Эти метеоданные находятся в
свободном доступе на серверах
Integrated Global Radiosonde Archive (Объединённый архив всемирных
измерений с радиозондов) [1]. Например, на Рис.
1 приведен фрагмент данных, передаваемых
радиопередатчиком метеозонда над территорией г. Болонья, Италия. Наряду со
служебной информацией метеозонд предоставляет следующий набор данных: давление,
геопотенциальная высота, температура, температура точки росы, направление
ветра, скорость ветра.
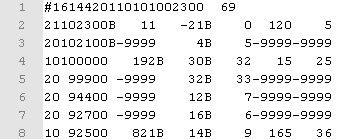
Рис. 1 Образец данных с метеостанции Болонья формата IGRA
Поскольку
метеозонд передает данные, привязанные к различным высотам (в диапазоне от 0
метров до 26 км.), возникает возможность изучения послойной картины параметров
атмосферы, но с частотой, привязанной к суточным метеонаблюдениям. В результате
оценить среднестатистические характеристики атмосферы исследуемого региона можно
не чаще, чем за характерные календарные периоды.
Нужно учитывать, что характер распределения
параметров различается для различных регионов и высот. Поэтому наиболее
ответственным этапом этого исследования является получение интегральных и
дифференциальных кривых распределения вероятности. Для построения этих характеристик
при обработке метеоданных определяются максимальное и минимальное значение этих
параметров, а также выбирается интервал варьирования. Его грамотный выбор
связан как с объемом выборки, так и с желаемой точностью оценки параметров
распределения. Малые интервалы приводят к неравномерному распределению
попаданий в них, а большие - к грубой оценке параметров распределения.
На Ошибка!
Источник ссылки не найден. приведен наглядный пример формирования дифференциальной
диаграммы плотности вероятности распределения значений скорости ветра в
приземном слое 0–300 метров с тремя вариантами выбора интервала. Данные
получены за счет первичной обработки результатов метеонаблюдений за период с
1-го января по 31 декабря 2011 года для города Болонья (Италия). Анализ
вариантов показывает, что интервал 0,5 м/с неоправданно мал, т.к. приводит к
появлению нулевого столбца даже в начальной (наиболее содержательной) части
диаграммы. Интервал 1 м/с неоправданно велик, т.к. приводит к смещению
очевидного скоростного максимума в диапазоне 0,75-1,5 м/с к существенно
меньшему значению в диапазоне 0-1 м/с. Поэтому интервал 0,75 м/с выбран как
наиболее эффективный.
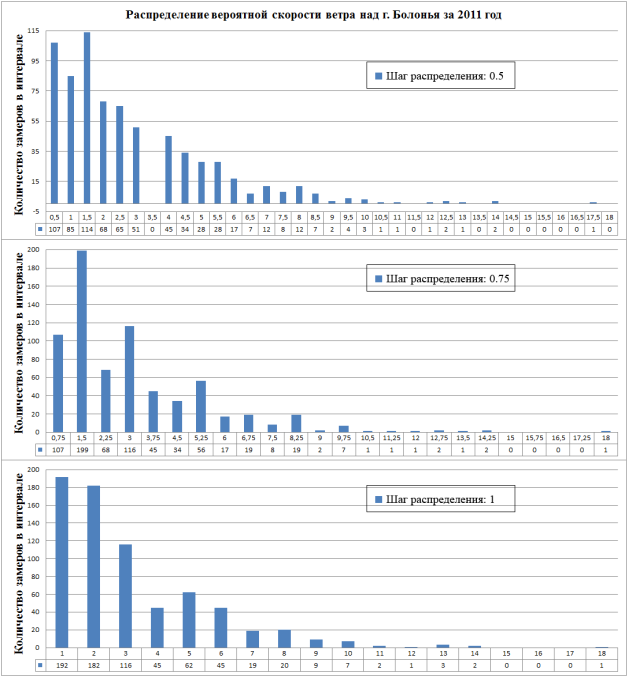
Рис. 2
Варианты дифференциального распределения вероятности силы ветра
Из диаграмм видно, что распределение
асимметрично. Это исключает возможность обработки данных с использованием
классических статистических критериев и оценок, базирующихся на гипотезе о
нормальности распределения случайной величины (СВ). Поэтому необходим
индивидуальный подход к решению поставленной задачи, основывающийся на базовых
вероятностных понятиях и оценках.
Так, наиболее информативным для решения
поставленной задачи выбора количественных характеристик распределения,
содержательных для составления плана исследований, видится понятие моды в
применении к интервальным представлениям характера распределения изучаемых
данных. Под модой некоторого набора данных понимается наиболее вероятное
значение изучаемого набора данных [2]. Следовательно, в данном случае она
составит ~1,125 м/с.
Кроме того, при решении конкретной задачи,
связанной с анализом распределения скорости ветра для имитационного
исследовании ЛА, нужно принять во внимание, что кривая распределения плотности
вероятности скорости ветра над Болоньей имеет очевидный многоэкстремальный
характер. Такое распределение в теории вероятностей называется «полимодальным»
[2]. Поэтому, его можно характеризовать векторной модой
![]()
где
![]() - мода
- мода ![]() -го интервального экстремума;
-го интервального экстремума; ![]() - количество
локальных экстремумов распределения.
- количество
локальных экстремумов распределения.
Для рассмотренного примера выделяются моды,
характеризующие: малые скорости (МС-интервал), средние скорости (СС-интервал),
повышенные скорости (ПС-интервал), высокие скорости (ВС-интервал). Наиболее
вероятная скорость ветра 1.125 м/с, наименее вероятная 12.75 м/с. Эти величины
были заложены в план эксперимента по исследованию аэродинамики ЛА,
разрабатываемого по спецпроекту Евросоюза (работа выполнена при поддержке
гранта Президента Российской Федерации № НШ-1557.2012.10, и в рамках
проекта МААТ – «Многоуровневая
транспортная система на базе стратосферных дирижаблей» в рамках Седьмой
рамочной программы FP7 Евросоюза).
Выводы. Использование кривой распределения
плотности вероятности и обработка ее при построении алгоритмом варьирования
интервала позволяет выявить распределение по диапазону наиболее вероятных
значений исследуемого параметра, что повышает эффективность плана эксперимента,
и информативность его результатов.
Литература
2. Вентцель Е.С., Теория
вероятностей / Е.С.Вентцель, — 4-е изд. — М. : Наука, 1969. — 576 с., 4 изд.