Математика/1. Дифференциальные и интегральные уравнения

Ismagul R.S.

Kostanay State University Ahmet Baitursynov, Kazakhstan

SHORTENING METHOD FOR FINDING A SOLUTION OF

A COUNTABLE SYSTEM OF INTEGRODIFFERENTIAL EQUATIONS

This article gives a review of finding a solution of a countable system through shortening method. It describes necessary and sufficient conditions for uniqueness of an almost multiperiodic solution of integrodifferential equations in partial derivatives.
        Let’s introduce some notations and definitions:
 - The class of n-dimensional -functions, -satisfying the conditions.

and almost multiperiodic in с - vector- almost period , where when ; countable-dimensional vector, where; W_m и V_m - functionals that assign vectors W_m = ( φ₁, …, φ_т, 0,…) и V_m = ( 0,…,0, φ_m+1,φ_т+2, …) to the vector φ = (φ1, ..., φt, ...).

Let’s consider a system of integrodifferential equations of the form
, (1)
 where x, Q, R are n-vectors-columns; P (t, φ) is a matrix of dimension n × n, φ = (φ1, ..., φt, ...) is a countable vector, and , >0 are small parameters.
Let’s consider that the conditions [1,c.168] и () are met if:
1) vector-function is bounded and contiguous with all
variables, and has limited contiguous derivatives of first order in ,; diagonally - almost in period, belongs to -class evenly relatively to;

2) continuous function provides improper integral, where is permanent.

Let’s contemplate the differential operator:

.

To reduce the record we’ll take . It should be noted that the coefficients of Lipshitce enhanced condition for vector-function are .

Let’s contemplate the linearized equation:

. (2)

Let be the characteristic function of the functional, which satisfies the integral equation

.
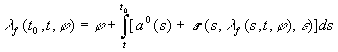For characteristic function there are rates analogous to relations of the form I(a-b) и 1⁰-9⁰ [1].

Let’s consider the functional Т, representing each vector-function in vector-function

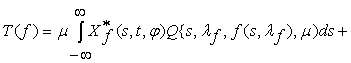
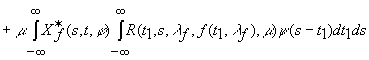
, where

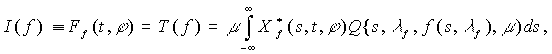
which is known from [1].

We will study

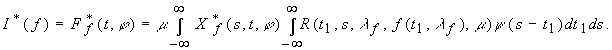
Considering that , we can write . From rates III(a-d) [1,c. 171] we can conclude that there is such a number , for which with all there are the following relations:

1) ,

2) ,

3) ,

4) .

Thus, we come to the statement of theorem 1.

Theorem 1. If the conditions , are met for the equation (1), than for all the meanings, equation (1) has a single almost multiperiodic solution from the class , converging in a zero vector with .

Let’s consider a system shortened in φ, obtained from (1):

, (3)

where is a shortened differential functional. Then 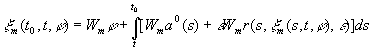is a characteristic function of the functional .

Then we can see that an almost multiperiodic solution of the basic system (1) can be evenly approximated by an almost multiperiodic solution of the system in of the form (3).

Theorem 2. If the equation (2) is uncritical and the conditions , for the quantities are met, then the equations (1) and (3) with and with have a single almost multiperiodic solution, respectively, and at that we have the relation

in the sense of convergence in the form [2], where .

REFERENCES:

1. Umbetzhanov D.U. Almost periodic solutions of evolution equations. Alma-Ata, Nauka, 1990, 188 p.

2. Ismagul R.S., Ramazanova A.T. About a countable system of some differential equations in partial derivatives // Materials of international scientifically-practical conference of students, graduates and young scientists "Lomonosov-2009" .- Astana, 2009, .51-53.