Математика/ 1. Диференціальні і інтегральні рівняння

К.ф.-м.н. Р. І. Собкович, к.ф.-м.н. А.І. Казмерчук

Прикарпатський національний університет імені В.Стефаника

Розв’язання нелінійної багатоточкової задачі для диференціальних рівнянь першого порядку

Розглянемо диференціальне рівняння

, (1)

де функція визначена та неперервна в області , і поставимо задачу відшукання його розв’язків, які задовольняють умові

, …, (2)

де - певна функція, яка пов’язує невідомі значення розв’язку в заданих точках . Дослідження даної задачі тісно пов’язане з методами роботи [1].

Введемо позначення , де - деякі параметри. Очевидно, що

.

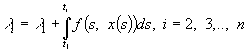Після заміни

,

рівняння (1) набуде виду

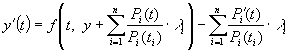. (3)

Виконана заміна дозволила звести задачу (1), (2) до відшукання функції , яка є розв’язком рівняння (3) та задовольняє однорідним умовам

, (4)

а також до знаходження значень параметрів , при яких виконуються рівності

, (5)

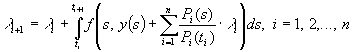. (6)

Запишемо рівняння (3) в дещо іншому виді. Для цього зробимо наступні перетворення.

.

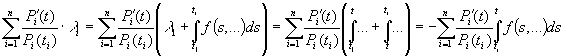Вони ґрунтуються на очевидних тотожностях та 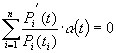(- довільна функція). Поряд із диференціальним рівнянням

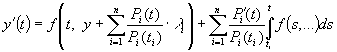, (7)

розв’язки якого повинні задовольняти умовам (4), розглянемо інтегральний оператор , визначений рівністю

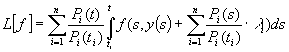. (8)

Оскільки довільну неперервну на відрізку функцію даний оператор переводить у певну неперервно диференційовну на даному проміжку функцію , яка задовольняє умовам і , то задачу (4), (7) можна замінити інтегральним рівнянням

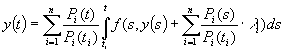, (9)

а задачу (1), (2) – системою рівнянь (9), (5) та (6).

Розв’язком системи (9), (5), (6) будемо називати множину , якщо функція визначена та неперервно диференційовна на проміжку , елементи даної множини тотожно задовольняють рівняння (9) та рівності (5), (6), а також значення та належать відрізку .

Встановимо умови існування розв’язків задачі (9), (5), (6).

Нехай для двох довільних точок () та () для функції існують сталі та , при яких

, (10)

а також в областях визначення функцій та виконуються нерівності

(11)

, (12)

де та - деякі сталі.

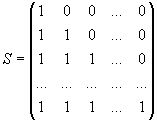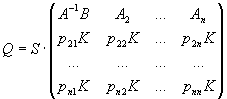Введемо в розгляд матриці та , де .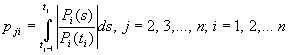

Теорема. Нехай виконуються умови (10) - (12), а також всі власні значення матриці лежать в одиничному крузі. Тоді система рівнянь (5), (6) для довільної неперервної на проміжку функції має єдиний розв’язок .

Література:

1. Собкович Р.І., Казмерчук А.І. Розв’язність багатоточкових крайових задач з параметром для системи диференціальних рівнянь. - Карпатські математичні публікації.-2010.-Т.2.-№2.-с.116-122