Математика/5. Математическое моделирование

 

Махамбетова Г.И.

Костанайский гос.  университет им.А.Байтурсынов, Казахстан

НАХОЖДЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ДЛЯ ОДНОРОДНОГО ГРУНТА

Экспериментальное и численное определение коэффициента теплопроводности является самостоятельной задачей современной теорий геокриологии. В настоящей работе описан алгоритм с помощью, которой определяется коэффициент теплопроводности однородного грунта.

1. Постановка задачи. В области , ,  изучается задача                           ,                                               (1)

                   ,     ,                     (2)                        

                                        ,                             (3)

Требуется определить коэффициент теплопроводности,  используя условие

                                        ,                              (4)

Для решение поставленной задачи, в работе /8/ нами была предложена приближенная задача для температуры и сопряженная задача с помощью, которая составляется градиент функционала.  Приближенная задача имеет вид:                                                                               (5)

                                                            (6)

                                                              (7)

 Где,  является разностный аналог температуры . Причем  соответственно шаги по пространственным координатам и по времени. В дальнейшем  будем пользоваться обозначениями . Задача (5)-(7) изучается в сеточной области  

Сопряженная задача  , ,                                               

Расчетные формулы определения

1) Задается начальное приближение

2) Решение прямой задачи

  2.1 Вычисляются коэффициенты разностей задачи.

               .

  2.2 Вычисляются краевые условия для  и

      

  2.3 Определяются коэффициенты проточной прогонки по формуле

,   , при всех i=N-2,N-3,…,0.

2.3 Вычисляется начальное условие поток температуры

2.5 Вычисляется поток температуры.

 для всех i=1,2,…,N-1.

3) Решение сопряженной задачи

3.1 Вычисляются коэффициенты  

3.2. Начальное условие коэффициента метода прогонки =А; =0

3.3.          Вычисляются коэффициенты метода прогонки ,

,  при всех i=2,3,…,N.

3.4 граничные условия поток температуры              

3.5 Поток сопряженной задачи              

3.6 Вычисление температуры грунта

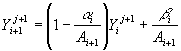 i=0,1,2,…,N-1., 

4) Вычисляется градиент функционала         

5) Следующее приближение коэффициента теплопроводности вычисляется по формуле

6) Вычисляется функционал     

7) Если 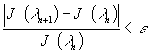,  то процесс вычисления прекращается, и за приближенное значение коэффициента теплопроводности принимается .

Литература

1        Мартынов Г.А. Тепло - и влагоперенос в промерзающих и оттаивающих грунтах. Основы геокрилогии (мерзлотоведения). – М.: 1959, под. ред. Н.А. Цытович. гл. VI стр. 153-192.

2          Чудновский А.Ф. Теплобмен в дисперсных средах. – М. Гостехиздат, 1954, 444 с.

3        Жумагулов Б.Т., Рысбайұлы Б., Адамов А.А. Сходимость разностной схемы для обобщенной задачи Стефана конвективного распространения влаги // Вестник НАН РК. 2007. - №5. - С. 30-41.

4        Рысбайұлы Б., Адамов А.А. Исследование теплопроводности фазовой зоны в многослойном грунте  // Вестник НАН РК. 2007. -№4. - С. 30-33.

5        Рысбайулы Б., Байманкулов А.Т., Махамбетова Г.И.  Обратная задача кондуктивного распространения тепла в однородной среде// Вестник НАН РК, 2008, №1. 

6        Рысбайулы Б., Маханбетова Г.И. Разностная схема для обратной задачи кондуктивного распространения тепла в однородной среде // ДАН РК, 2008, №1.