Степанова Е.И.
Южный филиал
Национального университета биоресурсов и природопользования Украины «КАТУ»,
Украина
Исследование
упругопластических контактных взаимодействий в среде MatLab 7.10.01.
Рассматривается
проблема моделирования упругопластического контактного взаимодействия тела
сферической формы с поверхностью. Для получения математических описаний,
предложена некоторая механореологическая модель процесса, основанная на
контактных взаимодействиях плодов томатов с элементами конструкций овощеуборочных
агрегатов.
Ключевые слова: упругопластическое контактное взаимодействие,
механореологическая модель процесса, реологические уравнения поведения системы,
численный метод Рунге-Кутта.
Постановка
проблемы. Задача
проектирования поверхностей контакта плодов томатов в овощеуборочных агрегатах
фактически относится к классу обратных задач проектирования. Именно по динамике
процесса и физико-механическим свойствам контактирующего тела необходимо
осуществить построение самой поверхности и подобрать материал. В этом аспекте
задача моделирования процессов упругопластических взаимодействий является в
значительной степени актуальной.
Анализ
источников. Известно
[1], что характеристики физических тел при контактном взаимодействии
существенно зависят от напряжений, возникающих в зонах их фактического
контакта. Важно отметить, что, несмотря на то, что упругопластические
деформации на реальных контактах широко распространены, они все еще не
достаточно исследованы из-за трудностей физического и математического
характера, которые приводят к необходимости различного рода упрощений.
Большинство, в том числе и современных публикаций об ударно-контактных
взаимодействиях твердых тел [2, 3, 4], в основном посвящены изучению процессов
на упрощенных моделях, либо связаны с построением эмпирических зависимостей. Менее
изучены взаимодействия упругопластических тел с поверхностями различных
(неплоских) конфигураций, в частности, упругопластических оболочек из
эластомеров или композитных материалов.
Основной
результат. В
[5] предложена контактная поверхность переходного узла между транспортерами
агрегата АУО-14, построенная в классе брахистохрон, с направляющей в виде
гипоциклоиды, что обеспечивает минимальное время процессов взаимодействия. При
этом, в основу моделирования процесса первого удара плода о поверхность
отражателя, предложена модель Г. Герца [6] в ее обобщении К. Ханта и Ф. Кроссли
[7]. Дальнейшие
обобщения модели Г. Герца привели к уравнению [5]:
, (1)
где
масса тела, 
упругая сила взаимодействия при ударе, такая, что:
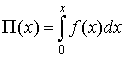, (2)
где
потенциальная энергия упругой деформации. Решение получено в
квадратурах на основе специальных функций Ламберта. Однако является очевидным,
что предложенная модель требует определенной детализации и уточнения.
Важно отметить, что один из путей уточнения
описания реологическими уравнениями поведения реальных материалов под
нагрузками – это путь описания свойств как комбинации тех или иных идеальных
свойств. Например, вязкий материал – идеальный ньютоновский, пластичный – тоже
идеальный Сен-Венановский материал [8]. При этом, если приложение определенного
напряжения величины 
вызывает вязкое
течение материала с пластической вязкостью 
, то реологическая модель такого поведения известна в
литературе как тело Шведова-Бингама.
Для моделирования контактного взаимодействия плода
томата с поверхностью отражателя (приемного бункера) АОУ-14 приняты следующие
допущения. Контактирующее тело (томат) – сферическое тело, а поверхность
контакта – плоскость. Схема упруго-вязкопластической модели приведена на рис.
1.
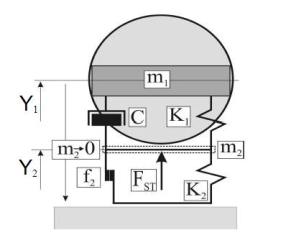
Рис. 1.
Модель включает два последовательных блока:
упруго-вязкий – К1-С и упругопластический – К2-f2. Блок К1-С
описывает упругие деформации системы и учитывает возникающие при этом потери
энергии с помощью демпфера С. Сила сопротивления нелинейного вязкого элемента С
зависит от скорости и величины деформации.
Блок К2-f2 описывает пластические
деформации и учитывает возникающие при этом потери энергии. Установка элемента f2 параллельно с упругим
элементом К2 обеспечивает более полное моделирование явления
уплотнения материала, которое характеризуется ростом усилия с увеличением
пластической деформации.
Масса сферического тела сосредоточена в
инерционном элементе m1, массой элемента m2 можно пренебречь (m2®0), так как он не
оказывает существенного влияния на динамику рассматриваемой системы (введена в
рассмотрение для удобства математических описаний).
На начальном этапе ударного взаимодействия,
очевидно, возникают только упругие деформации, поэтому деформации подвергается
только упруго-вязкий блок. Дифференциальное уравнение движения системы имеет
вид:
, (3)
Упругопластический блок включается в работу,
когда динамическое усилие достигает заданного значения FST, соответствующего
интенсивному появлению пластических деформаций. Дифференциальные уравнения
движения системы имеет вид:
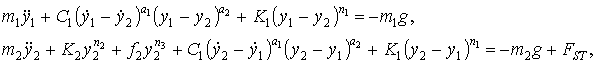(4)
где
перемещение и скорость масс 
и 
; 
коэффициенты
жесткости упругих элементов модели; 
коэффициент вязкости вязкого элемента модели; 
коэффициент сдвига упругопластического блока модели; 
усилие, соответствующее началу образования пластических
деформаций.
Все элементы модели имеют нелинейные
характеристики. Это расширяет возможности модели и позволяет более детально
исследовать влияния нелинейных характеристик элементов модели на динамику ее
ударного взаимодействия. Для конкретных значений степенных показателей для
упругой составляющей при ударном взаимодействии сферического тела их следует
принимать 
, пластическую составляющую можно приближенно принимать
пропорциональной действующей силе, т.е. 
.
Очевидно, что система (4) после неособых
преобразований: 
и 
, примет вид:
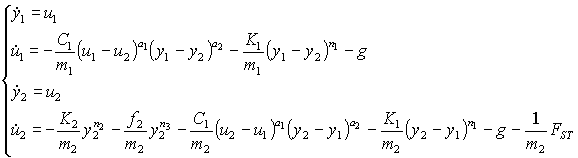(5)
Для интегрирования системы (5) применена
процедура метода Рунге-Кутта 4-го порядка реализованная в среде MatLab
7.10.01. Ниже приводится М-файл с данными для системы (5), основная программа и
график решения:
М-файл
function dy = rigid1(t,y)
dy = zeros(4,1); % a column vector
C = 0.5;
m = 75;
M = 100;
K1 = 0.2;
K2 = 0.5;
a1 = 0.5;
a2 = 1.5;
n1 = 1.5;
n2 = 1.5;
n3 = 1.0;
g = 9.8;
f = 3.14;
FST = 10.0;
dy(1) = y(3);
dy(2) = y(4);
dy(3) = - (C / m) * (y(3) - y(4)) ^ a1 *
(y(1)-y(2)) ^ a2 - ...
(K1 /
m) * (y(1) - y(2)) ^ n1 - g;
dy(4) = - (K2 / M) * y(3) ^ n2 - (f / M) * y(3)
^ n3 - ...
(C /
M) * (y(4) - y(3)) ^ a1 * (y(2) - y(1)) ^ a2 - ...
(K1 /
M) * (y(2) - y(1)) ^ n1 - g - FST / M;
end
Основная программа
>> options =
odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5 1e-5]);
>> [T,Y] = ode45(@rigid1,[0 200],[0 0 0.1 0],options);
>> plot(Y(:,1),Y(:,2),'*');
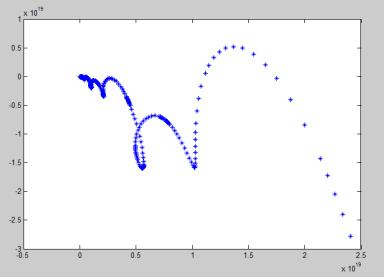
Рис. 1 –График решения в переменных 
и 
.
Выводы
Построенная физическая модель объекта и
математическая модель процесса позволит осуществить имитационные эксперименты
ударного вязко-упругопластического взаимодействия, на основе которых с учетом
определенных эмпирически характеристик (исходных данных) осуществить подбор
соответствующих физико-механических и уточнение геометрических характеристик
поверхности контактов.
Список
литературы
1. Максименко А.А.,
Котенева Н.В., Перфильева А.Д. Исследование нормальных напряжений при
упругопластическом контактном взаимодействии // Ползуновский вестник, 2009. – №
1-2. – С. 264-266.
2. Дрозд М.С. Определение
механических свойств металла без разрушения. – М.: Металлургия, 1965. – 171 с.
3. Булычев С.И. О
корреляции диаграмм вдавливания и растяжения // Заводская лаборатория.
Диагностика материалов, 2001. – Т. 67. – № 11. – С. 33-41.
4. Ишлинский А.Ю., Ивлев
Д.Д. Математическая теория пластичности. – М.: ФИЗМАТЛИТ, 2003. – 704 с.
5. Степанова Е.И. К задаче
проектирования переходных узлов рабочих органов сельскохозяйственных агрегатов
для уборки овощей на основе математической модели вязкоупругого взаимодействия
// MOTROL (Motorization and
power industry in
agriculture), Lublin, 2010. – T.
12D. – P. 232-239.
6. Hertz H. Über die Berührung fester elastischer Körper //
Jornal reine und angewandte Mathematik. – 1882. – B. 92. – S. 156-171.
7. Hunt K.H., Crossley F.R.E. Coefficient of restitution interpreted as
damping in vibroipact // ASME Journal of applied mechanics. – 1975. – № 6. – Р. 440-445.
8. Ильюшин А.А.
Пластичность / Часть 1. Упруго-пластические деформации. – М.: ОГИЗ. – 1949. –
376 с.