Панченко Р.Н.

Национальный технический университет Украины «КПИ»

О ДИНАМИКЕ ПРЯМОУГОЛЬНОЙ МЕМБРАНЫ

Экспериментальные и теоретические исследования последних лет существенно расширили и вывели на качественно новый уровень представления о характере и природе рассеяния энергии звукового поля в механических системах. Вместе с тем остается много нерешенных проблем качественной и количественной оценки взаимодействия избыточного давления с бортовой аппаратурой. Ряд комплектующих элементов бортовой аппаратуры летательных аппаратов изготовляют в виде идеально гибких, постоянной толщины пластин (прямоугольных или круглых), однако сильно и равномерно растянутых во всех направлениях, так что можно пренебречь малыми изменениями этих усилий, вызванных их прогибами при колебаниях. Такие элементы называют мембранами. Рассмотрим прямоугольную мембрану со сторонами и .

Независимо от вида функции в пределах прямоугольной области ее всегда можно представить в виде двойного ряда

,

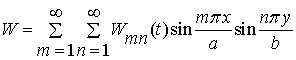где , – числа полуволн изгиба в направлении оси и соответственно. Каждый член ряда удовлетворяет граничным условиям –

.

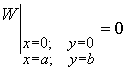Вынужденные колебания мембраны описываются дифференциальными уравнениями вида:

,

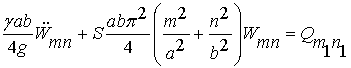где – обобщенная сила, определяемая из формулы для виртуальной работы волны избыточного давления на виртуальном перемещении ; , – числа полуволн избыточного давления в направлении осей и ; – равномерно приложенное растягивающее усилие; – удельная масса материала мембраны; – ускорение свободного падения.

Пусть

,

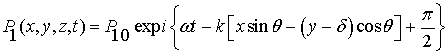где – амплитуда избыточного давления; – круговая частота падающей волны; – волновое число; – скорость звука в воздухе; – угол падения плоской волны на лицевую поверхность мембраны; – толщина мембраны; ,  – координаты точки поверхности.

Тогда,

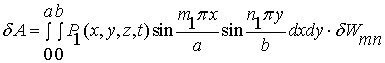
и

,

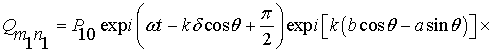
где , – постоянные коэффициенты.

Если при мембрана находилась в покое, то внезапное воздействие , прикладываемое равномерно ко всей поверхности, приводит к динамическим прогибам вида

,

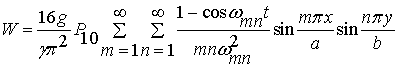где , - нечетные числа, - квадрат круговой частоты изгибных колебаний -й формы.

В том случае, когда граница мембраны несколько отличается от круговой, частота низшей формы колебаний мембраны примерно равна частоте круговой мембраны, имеющей ту же площадь и то же значение величины . В общем случае для определения частоты основной формы колебаний мембраны можно принять в виде

,

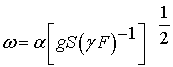где – площадь мембраны. Если же мембрана закреплена не только по граничной окружности, аналитическое исследование динамики возмущенного движения при волновом воздействии представляет значительные математические трудности. В настоящее время получено решение только для случая эллиптической границы.

Воспользовавшись методикой [1] получим закон изгибного движения мембраны под действием избыточного давления –

.

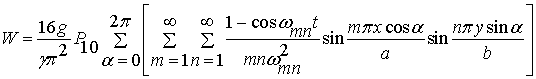Анализ этого выражения показывает, что узловые диаметры мембраны находятся на линиях и .

Примем для конкретности , ( - радиус мембраны). В этом случае для низшей формы имеем

.

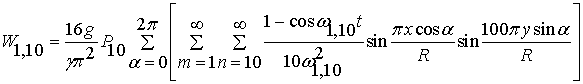Откуда, в общем случае получаем возможность установить точки мембраны, где имеет место суперпозиция нескольких форм колебаний –

.

На линиях и определяем узловые диаметры мембраны.

Интересно отметить, что кроме узловых диаметров, мембрана может иметь и узловые окружности, на которых величины прогибов .

Исследовав закон изгибных колебаний на экстремум, можно установить также линии пучностей , где прогибы мембраны достигают своих максимальных значений –

;

.

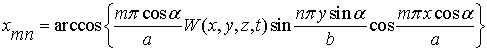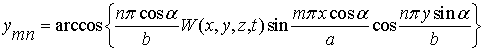Литература:

1. Мельник В.М., Карачун В.В. Шуми і вібрація. Збурюючі чинники та їх характеристики.Навч. посібник. –К.: Техніка, 2008. -352 с.