MATHEMATICS / 4

MATHEMATICS / 4. Applied mathematics

PhD Iskakova A., Toksanova S.

L.N. Gumilev Eurasian National University, Astana, Kazakhstan

Probabilistic model of the dynamics of social cases

Presented probabilistic model reveals the need for surveillance issue detailed approach to the study of factors affecting the dynamics of the recipients of social cases.

1. Intorduction. Obviously, the dynamics of the receipt of social benefits affect the following factors: economic (inflation, crisis, changes in the sectoral structure of the economy), social (health condition, change of residence etc) and psychological factors (intuziazma loss, loss of interest in work, new hobbies and motivation).

Probabilistic study of all quantitative indicators for social benefits is based on the likely impact of the relevant factors. Of course the theory of probability it is clear that these factors can be considered as a polynomial distributed. However, the probability distribution of the sum polynomial distributed random variables and its application in social studies in the scientific literature in [1, p. 79], [2, p. 012,113], [3, p. 86].

However, if you are risen situations in which events were to issleduemmye imposition of unknown phenomena, in other words, the implicit assumption that there are still many unsolved problems.

2. Construction of a probabilistic model of events dependent factors. Any social benefits is a consequence of the influence of group factors. Let us assume that the social case u case N factors with some degree of action. We define each factor is one of the possible numbers l₁, l₂, ..., l_n with the corresponding values of the probabilities p₁, … , p_n and

Let’s k factors can contribute to the possible implementation of the u social case. And l₁ factor influenced the social event u r₁ times, l₂ factor influenced the social event u r₂ times, and so on factor l_n influenced social event u r_n times. It's obvious that

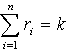Theorem 1. The number of all kinds of influences k factors with repetitions in which l₁ factor influenced the social event once u r₁, l₂ factor influenced the social event u r₂ times, and so on factor ln influenced social event u r_n times, defined as

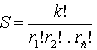The proof is obvious from the course of combinatorics (see. [4, p. 19]).

Theorem 2. The probability that in the case of social impact u k factors with repetitions in which l₁ factor influenced the social event's time r₁, l₂ factor influenced the social event u r₂ times, and so on factor ln influenced social event u r_n times, there

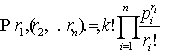, (1)

where the values p₁, … , p_ndetermine the probability factor of influence with the corresponding number l₁, l₂, ..., l_n on sogial case u.

Proof. Obviously, in this case we have a probability polynomial distribution, which has the form (1) (see. [5, c.223]). QED.

Ex. 1. In reviewing the analysis of the dynamics of social benefits in the event of job loss in the North-Kazakhstan region we have the data presented in Table 1.

Table 1.

Dynamics of recipients of social payments in case of job loss in the North-Kazakhstan region

Years	2007	2008	2009	2010	2011	2012	2013	2014	2015
Number of recipients	30	110	1200	1100	1230	1005	1150	1320	1030

Let us assume that the economic factor can affect the loss of a job with probability 0.7, the 2nd factor of 0.2, 3rd - 0.1. Suspected breaking the factors affecting the dynamics of the job losses, on the North Kazakhstan region are presented in Table 2.

Table 2.

Suspected breaking the factors affecting the dynamics of the job losses, the North Kazakhstan region

Years		2007	2008	2009	2010	2011	2012	2013	2014	2015
Number of recipients		30	110	1200	1100	1230	1005	1150	1320	1030
Variant 1	Factor 1	21	77	840	770	861	703	805	924	721
	Factor 2	6	22	240	220	246	201	230	264	206
	Factor 3	3	11	120	110	123	101	115	132	103
Variant 2	Factor 1	22	82	900	825	922	753	862	990	772
	Factor 2	7	25	276	253	282	231	264	303	236
	Factor 3	1	3	34	22	26	21	24	27	22

Breaking the factors there is a significant set. So for the first embodiment of partitions factors have for 2007

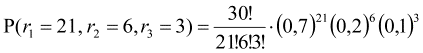3. The probability distribution of the sum of the factors affecting the social event. For example, we have social benefits with the value of u, k represents the sum of the values of the factors that will affect u social benefits. I.e

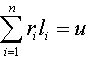. (2)

Theorem 3. The probability that the sum of the numbers on the k factors affect repetition on social benefits equal to u, is determined by the formula

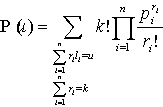Proof. Needless to say, if the formula (2) takes place then system of equitions

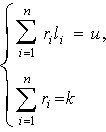
has one or more solutions. The probability of each solution of last system is determined by Theorem 3. Thus, come to the proof of the theorem. QED.

Ex. 2. From Example 1 we have only two options partitions factors are shown in Table 2. Consequently, the next decision fair.

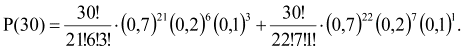
References:

1. Искакова А. С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии //Сибирский журнал индустриальной математики. – 2002. – Т. 5. – №. 1. – С. 79-84.

2. Ayman I. Construction of the most suitable unbiased estimate distortions of radiation processes from remote sensing data //Journal of Physics: Conference Series. – IOP Publishing, 2014. – Т. 490. – №. 1. – С. 012113.

3. Iskakova A., Ibragimov B. A method for determining an unbiased estimate // Nauka i Studia. – Przemyśl: Nauka i studia. - NR 7 (52), 2012. –P. 86-91.

4. Сачков В. Н. Комбинаторные методы дискретной математики. – Издательство" Наука", Главная редакция физико-математической литературы, 1977.

5. Panaretos J., Xekalaki E. On generalized binomial and multinomial distributions and their relation to generalized Poisson distributions. // Ann. Inst. Math. 1986.V.38.Part A. P. 223 – 231.