Математика.Дифференциальные и интегральные уравнения

Яскилка О.А.

Донецкий национальный университет экономики и торговли имени

Михаила Туган-Барановского, Украина

Применение матриц в экономике

В данной статье мы рассмотрим использования матриц в экономике. Для этого нам необходимо будет проанализировать решения экономической задачи и сделать определенные выводы.

Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами.

Понятие матрицы и основанный на нем раздел математики - матричная алгебра - имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное - компактной матричной форме.

С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.):

Ресурсы	Отрасли экономики
	Промышленность	Сельское хозяйство
Электроэнергия	5,3	4,1
Трудовые ресурсы	2,8	2,1
Водные ресурсы	4,8	5,1

Может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:

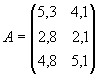
В данной записи, например, матричный элемент а₁₁ = 5,3 показывает, сколько электроэнергии употребляет промышленность, а элемент а₂₂ = 2,1 - сколько трудовых ресурсов потребляет сельское хозяйство.

Рассмотрим следующую задачу: пусть предприятие выпускает продукцию трех видов: P₁, P₂, P₃ и использует сырье двух типов: S₁ и S₂. Нормы расхода сырья характеризуются матрицей:

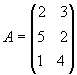
где каждый элемент а_ij (i = 1,2,3; j = 1,2) показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой С = (100 80 130), стоимость единицы каждого типа сырья (ден. ед.) - матрицей столбцом:

Рассмотрев задачу, получили: затраты 1-го сырья составляют S₁ = 2·100 + 5·80 + 1·130 = 730 ед. и 2-го - S₂ = 3·100 + 2·80 + 4·130 = 980 ед., поэтому матрица-строка затрат сырья S может быть записана как произведение:

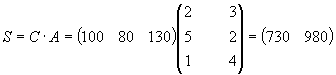
Тогда общая стоимость сырья Q = 730·30 + 980·50 = 70900 ден. ед. может быть записана в матричном виде: Q = S·B = (CA)B = (70900).

Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу:

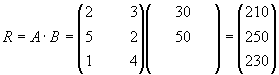
а затем общую стоимость сырья:

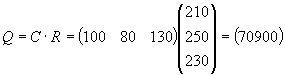
На этом примере мы убедились в выполнении ассоциативного закона произведения матриц: (СА)В = С(АВ).

Проанализировав использования матриц в экономике, мы пришли к выводу, что достоинства матриц состоят в том, что они используют широкий набор стратегически значимых переменных; указывают направление движения ресурсов. Среди недостатков этого инструмента: не обеспечивает реальных рекомендаций по разработке специфических стратегий; по ней невозможно определить сферы бизнеса, которые готовы стать победителями. Также матрицы позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.