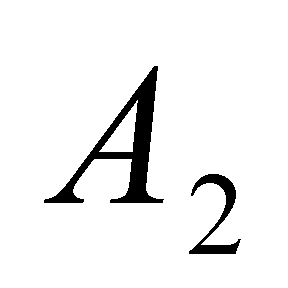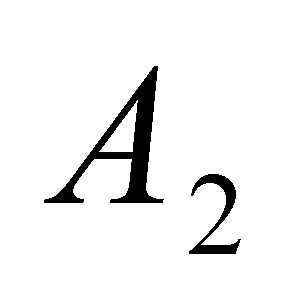Дулепов Е.Г., Ефремова А.Н.
Россия, Братский государственный
университет
Теорема как инструмент анализа логической состоятельности
утверждений
Предлагается инструмент
анализа логической состоятельности утверждений (знаний) в форме теоремы ![]() и приводятся методики
его использования для решения прикладных задач. В теореме через
и приводятся методики
его использования для решения прикладных задач. В теореме через ![]() обозначено общее
знание об объекте исследования, через
обозначено общее
знание об объекте исследования, через ![]() – заключение,
следствие, вывод, а через
– заключение,
следствие, вывод, а через ![]() – обобщенная посылка
или гипотеза.
– обобщенная посылка
или гипотеза.
Утверждение, истинность
которого доказана при условии ![]() предлагается считать логически
состоятельным. Таким условием может выступать, в частности, выполнение
полученного после формализации некоторого текстового документа в форме закона, договора, заявления, или его
истинности. Показано, что введение в структуру теоремы переменных и постоянных
величин делает ее не разовым, а постоянно действующим компьютерным
инновационным инструментом исследования.
предлагается считать логически
состоятельным. Таким условием может выступать, в частности, выполнение
полученного после формализации некоторого текстового документа в форме закона, договора, заявления, или его
истинности. Показано, что введение в структуру теоремы переменных и постоянных
величин делает ее не разовым, а постоянно действующим компьютерным
инновационным инструментом исследования.
Ключевые слова: логическая состоятельность утверждения, обобщенная посылка
теоремы, общее знание об объекте исследования.
Введение. Теорема
– математическое утверждение, истинность которого устанавливают или опровергают
с помощью доказательств.
Теоремы
логики высказываний доказуемы [1], отсюда следует возможность построения
универсального алгоритма доказательства теорем и преобразования последнего в
инструмент анализа логической состоятельности утверждений. Структура теоремы как инструмента
исследования и ее программная реализация частично изложены в [2,3].
Для
доказательства теорем в логике
высказываний чаще всего используют отношение порядка, которое существует между
причиной и следствием. Со времен Аристотеля отношение порядка, как более общее,
чем отношение эквивалентности, в форме правила вывода под латинским названием modus ponens широко использует современная логика и математика.
Теорема
может устанавливать существование различных бинарных отношений между двумя утверждениями ![]() и
и ![]() , в частности, отношений эквивалентности и порядка. Действительно,
существование двух теорем – прямой
, в частности, отношений эквивалентности и порядка. Действительно,
существование двух теорем – прямой ![]() и обратной
и обратной ![]() означает
существование отношения эквивалентности
означает
существование отношения эквивалентности ![]() , а существование одной из теорем
, а существование одной из теорем ![]() или
или ![]() – отношения
порядка.
– отношения
порядка.
Понятие
или знание о предмете можно рассматривать как множество признаков данного
предмета, однозначно выделяющих его из множества других предметов. Заметим,
признак отдельного предмета называют свойством, а признак, связывающий
несколько предметов – отношением.
Понятие
в форме множества не имеет истинностной оценки, однако имеет ее – в форме
тождественно-истинного логического произведения, сомножителями которого
являются тождественно-истинные выражения, утверждающие все эти признаки [4]. Такую
форму представления знаний в дальнейшем будем считать основной.
Постановка задачи. Рассмотрим структурную организацию теоремы как инструмента решения
прикладных задач и перечислим методики решения некоторых из их.
Теорема представляет собой
умозаключение в форме истинного условного предложения «если все посылки
или гипотезы f1, …, fk истинны, то истинным будет и заключение
или вывод fзак»:
f1 , … , fk ![]() fзак .
fзак .
Поскольку все
посылки в теореме истинны, то их
можно заменить одной
обобщенной
посылкой fоп , fоп = f1 ![]() …
…![]() fk , тогда теорема примет вид
fk , тогда теорема примет вид
fоп ![]() fзак
.
fзак
.
В отличие от импликации fоп ![]() fзак
в
теореме fоп
fзак
в
теореме fоп ![]() fзак посылка
fзак посылка ![]() , откуда следует, что область существования
теоремы fоп
, откуда следует, что область существования
теоремы fоп ![]() fзак – это область истинности обобщенной посылки
fоп .
fзак – это область истинности обобщенной посылки
fоп .
В рассматриваемом ниже универсальном
алгоритме доказательства теорем логики высказываний, каждая из функций f1 , …,
fk, fзак зависит от одного и того же набора
аргументов, часть которых может быть фиктивными. Если через ЕОП и ЕЗАК обозначить
области истинности fоп
и fзак , то критерий G существования
теоремы fоп ![]() fзак
будет означать выполнение условий (fоп
fзак
будет означать выполнение условий (fоп ![]() 0) и (fоп
0) и (fоп![]() fзак ) или условия (ЕОП
fзак ) или условия (ЕОП ![]() Ø)
Ø)![]() (ЕОП
(ЕОП ![]() ЕЗАК ), задаваемых предикатами:
ЕЗАК ), задаваемых предикатами:
G=(
fоп ![]() 0)&( fоп
0)&( fоп ![]() fзак) или G= (ЕОП
fзак) или G= (ЕОП
![]() Ø)
Ø)![]() (ЕОП
(ЕОП ![]() ЕЗАК ).
ЕЗАК ).
Универсальный алгоритм предполагает
выполнение следующих условий:
1. Определение набора всех попарно
различных аргументов функций для fоп
и fзак и вычисление
их совершенных ДНФ (СДНФ);
2. Вычисление
значения критерия G существования теоремы по формулам
G=(
fоп ![]() 0)
0)![]() ( fоп
( fоп ![]() fзак) или G
= (ЕОП
fзак) или G
= (ЕОП ![]() Ø)
Ø) ![]() ( ЕОП
( ЕОП ![]() ЕЗАК
).
ЕЗАК
).
Докажем,
например, логическую
состоятельность утверждения в форме известной
с древности сложной конструктивной дилеммы
![]() .
.
Решение.
1. Определяем набор (![]() ) аргументов дилеммы и СДНФ функций
) аргументов дилеммы и СДНФ функций
![]()
![]() ,
, ![]()
СДНФ![]()
СДНФ![]() ;
;
2. Определяем множества ЕОП
, ЕЗАК :
ЕОП ![]() Ø, ЕЗАК
=
Ø, ЕЗАК
=![]() и
и
вычисляем значение истинности
критерия G:
G=( fоп ![]() 0)
0)![]() ( fоп
( fоп ![]() fзак)
fзак)![]() или
или
G=( ЕОП ![]() Ø)
Ø)![]() (ЕОП
(ЕОП ![]() ЕЗАК ) =
ЕЗАК ) =
=(ЕОП
![]() Ø)&
Ø)&![]() .
.
Вывод:
логическая
состоятельность дилеммы доказана, так как ![]()
Компьютерное решение по
программе ![]() показано на рис. 1. В первой строке решения приведена
запись дилеммы на языке программирования, связь между логическими операциями и
символам языка устанавливает табл. 1.
показано на рис. 1. В первой строке решения приведена
запись дилеммы на языке программирования, связь между логическими операциями и
символам языка устанавливает табл. 1.
Таблица 1
|
И |
ИЛИ |
НЕ |
ЕСЛИ ТО |
Разделитель « |
|
& |
| |
! |
> |
; |
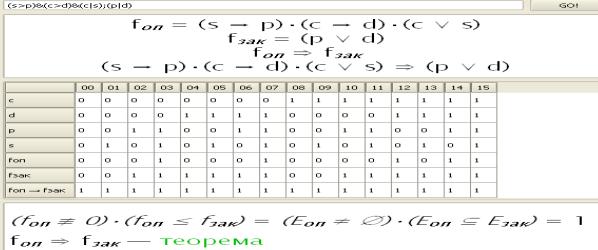
утверждение ![]() , программа
, программа ![]()
решение:![]()
Рис. 1 – Утверждение
дилеммы
Для построения инструмента
анализа логической состоятельности утверждений обобщенную посылку fоп в утверждении fоп ![]() fзак выразим через общее
знание
fзак выразим через общее
знание ![]() о предмете и гипотезу
о предмете и гипотезу
![]() , тогда утверждение будет иметь вид
, тогда утверждение будет иметь вид
![]()
В результате процедуры формализации
утверждения о гипотезах, общих знаниях и заключениях переводятся на язык
алгебры логики [2].
Гипотеза ![]() и заключение
и заключение ![]() в утверждении – величины
переменные, определяемые внешними причинами, например рынком, а общее знание о
предмете
в утверждении – величины
переменные, определяемые внешними причинами, например рынком, а общее знание о
предмете ![]() – величина
постоянная, она может быть определена логическим законом, договором, заявлением
и записана в форме решения логического уравнения
– величина
постоянная, она может быть определена логическим законом, договором, заявлением
и записана в форме решения логического уравнения ![]() или утверждена
теоремой
или утверждена
теоремой ![]() .
.
Вывод:
введение в структуру теоремы переменных и постоянных величин делает ее не разовым, а постоянно
действующим компьютерным инновационным инструментом исследования.
Покажем работу теоремы как
компьютерного инструмента при решении
следующих прикладных задач с помощью программы [3]:
1. Мониторинг коммерческого
договора;
2. Упрощение формул функций
алгебры логики;
3.
Выявление свойств функций и отношений между функциями.
Результаты решения прикладных задач
Задача №1. Мониторинг коммерческого договора:
Если курс доллара высок ![]() , то товар следует продавать в Китае
, то товар следует продавать в Китае ![]() , в противном случае
, в противном случае ![]() , товар следует
продавать в Братске»
, товар следует
продавать в Братске» ![]() . Договор – это общее знание:
. Договор – это общее знание: ![]() =
=![]() =
=![]()
![]() =
=![]()
![]() = 1.
= 1.
Cокр ДНФ Мин ДНФ
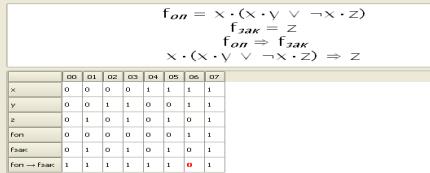
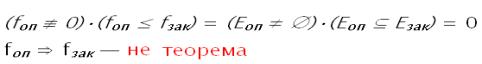
утверждение ![]() , программа
, программа ![]() , решение:
, решение:
договор будет нарушен, так как он предполагает продажу товара не в Китае, а
в Братске
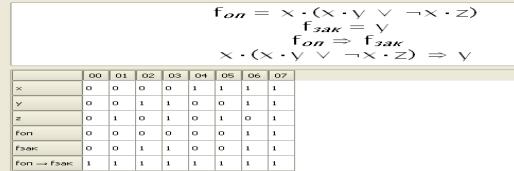
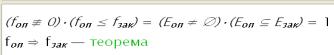
утверждение ![]() , программа
, программа![]() , решение:
, решение:
договор будет выполнен, так как он
предполагает продажу товара в Китае
Рис. 2 – Компьютерный
мониторинг договора
Компьютерное решение задачи
для ![]() и
и ![]() показано на рис. 2,
оно устанавливает выполнение или логическую состоятельность договора
показано на рис. 2,
оно устанавливает выполнение или логическую состоятельность договора ![]() .
.
Упрощение формул функций алгебры логики.
Необходимость решения подобных задач
возникает при мониторинге текстовых
документов после их формализации и при синтезе цифровых схем.
Рассмотрим компьютерное упрощение формул
функций алгебры логики
путем удаления лишних сомножителей, не равных единице в произвольных логических произведениях, и слагаемых, не
равных нулю в произвольных логических суммах.
Для выявления лишних
сомножителей в произведении и лишних слагаемых в сумме можно использовать
универсальный алгоритм доказательства и опровержения утверждений профессора
Дулепова Е.Г. [4]:
1. Если ![]()
![]()
![]() – теорема, то слагаемое
– теорема, то слагаемое ![]() –
лишнее;
–
лишнее;
2. Если ![]()
![]() – теорема, то сомножитель
– теорема, то сомножитель ![]() –
лишний.
–
лишний.
Задача
2. В логической сумме ![]() определить являются
ли лишними слагаемые
определить являются
ли лишними слагаемые ![]() и
и ![]() .
.
Компьютерные решения задачи показаны на рис. 3.

утверждение![]() , программа
, программа![]() , решение:
, решение: ![]() , слагаемое
, слагаемое ![]() - нелишнее
- нелишнее
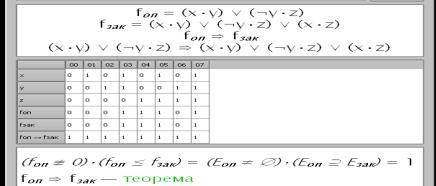
утверждение![]() , программа
, программа![]() , решение:
, решение:
![]() , слагаемое
, слагаемое ![]() - лишнее
- лишнее
Рис. 3 – Компьютерное
упрощение логической суммы ![]()
Задача
3. В произведении ![]() определить являются
ли лишними сомножители
определить являются
ли лишними сомножители ![]() и
и ![]() .
.
Компьютерные решения задачи показаны на рис. 4.
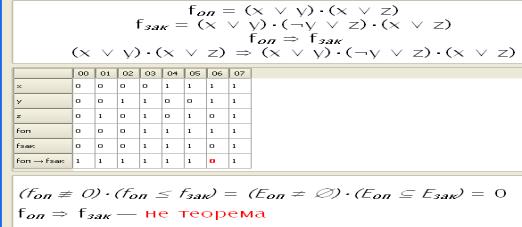
Утверждение ![]() ,
,
программа![]() ,
,
решение: ![]() , сомножитель
, сомножитель
![]() - нелишний.
- нелишний.

утверждение![]() ,
,
программа ![]() ,
,
решение: ![]() , сомножитель
, сомножитель
![]() - лишний.
- лишний.
Рис. 4 – Компьютерное
упрощение логического произведения ![]()
Выявление свойств функций и отношений
между функциями.
Бинарные
отношения эквивалентности ![]() между
между ![]() функциями
функциями ![]() и
и ![]() означают
существование двух теорем – прямой
означают
существование двух теорем – прямой ![]() и обратной
и обратной ![]() , а отношения порядка – только одной из теорем
, а отношения порядка – только одной из теорем ![]() или
или ![]() .
.
Как следует
из решений задач 3 и 4, пары функций ![]() и
и ![]() ,
, ![]() и
и ![]() связаны отношением порядка, а пары функций
связаны отношением порядка, а пары функций ![]() и
и ![]() ,
, ![]() и
и ![]() – отношением
эквивалентности.
– отношением
эквивалентности.
Задача 4. Установить является ли функция ![]() самодвойственной?
самодвойственной?
Решение. Функция ![]() является
самодвойственной, если она равна двойственной по отношению к ней функции
является
самодвойственной, если она равна двойственной по отношению к ней функции ![]() , то есть если
, то есть если ![]()
![]()
Компьютерное решение показано на рис. 5.

Утверждение
![]()
![]()
программа ![]()
решение: ![]()
![]()
Рис. 5 – Компьютерное
установление самодвойственности
Выводы
1. Теоремы логики высказываний доказуемы,
отсюда следуют возможности построения
универсального алгоритма для
доказательства теорем и преобразования его в инструмент анализа логической
состоятельности утверждений.
2. Понятие, представленное в форме множества,
не имеет истинностной оценки, однако в форме тождественно-истинного логического
произведения, сомножителями которого являются тождественно-истинные выражения,
утверждающие все эти признаки оно имеет ее.
3. Введение в структуру теоремы
переменных величин в виде гипотезы и
заключения, определяемых, например, рынком, и постоянной величины,
представляющей собой общее знание, например, в форме некоторого закона,
договора, заявления делает теорем не разовым, а постоянно действующим
компьютерным инновационным инструментом
исследования;
Литература:
1. Gentzen K. Untersuchungen
über das logische Dchlissen, Math. Zeitschrift, 1934 – 1935. T. 39.
2. Дулепов
Е.Г., Ефремова А.Н. Структура и возможности
универсального алгоритма
доказательства теорем, // Системы. Методы. Технологии: научный
периодический журнал № 2(10). – Братск:
ГОУ ВПО «БрГУ», 2011. C.71–73.
3. Свидетельство о
государственной регистрации программы для ЭВМ “Анализ логической состоятельности
договора» (AnCont v. 1.00) / Витковский
С.Л., Дулепов Е.Г., Кравченко Е.В.
Заявка № 2013610966. Зарегистрировано в Реестре программ для ЭВМ 9 января 2013
г.
4. Е.Г. Дулепов. Теоретические
основы вычислительной техники: Монография,
Братс. гос. унт. – Братск, 2008.–236с: ил.– Библиогр. 14 назв. – Рус. – Деп. в
ВИНИТИ. 04.07.2008, № 578 – В2008.