Математика / 3. Теория вероятностей и математическая статистика

к.ф.-м. н. Калжанов М.У.

Костанайский государственный университет

имени А.Байтурсынова

Измерение форм законов распределения при образовании композиций

Особенность законов распределения случайных величин как результатов измерения погрешности приборов и состоит в их большом разнообразии. Это обусловлено тем, что общая погрешность результата измерения или прибора определяется из ряда составляющих.

В том случае, если составляющие рассматривать как случайные величины, то суммирование погрешностей сводится к суммированию случайных величин. Относительно суммирования случайных величин законы их распределения меняют форму.

Закон распределения суммы независимых случайных величин , имеющих распределения р₁х и р₂х, называются композицией и выражается интегралом свертки:

Измерение формы законов распределения при образовании композиций происходит следующим образом:

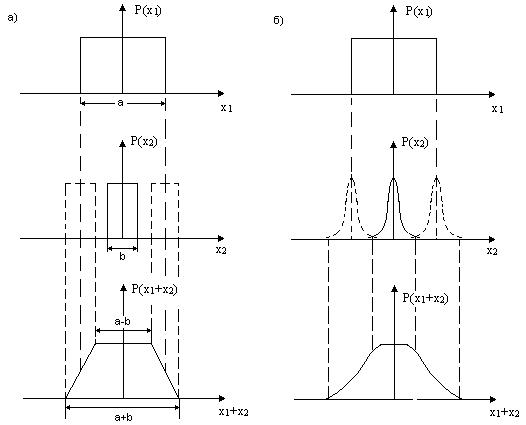
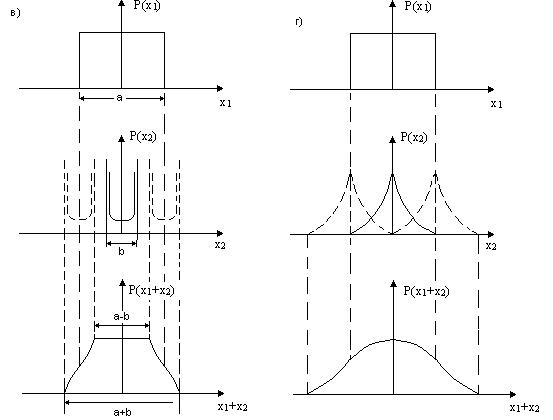
Рис.а) при суммировании двух равномерно распределенных погрешностей с шириной распределения а > в результирующая погрешность имеет распределение в виде трапеции с верхним основанием а-в и нижним а+в. Данную деформацию можно представить как размывание резко ограниченных хвостов более широкого распределения (шириной а) на величину протяженности в менее широкого распределения.

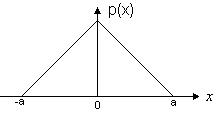
Композиция двух одинаковых (с шириной а) равномерных распределений является треугольной.

при –а ≤ х ≤ 0

= при 0 ≤ х≤ а

0 при –а > x; x >a

Это так называемое распределения Симпсона. Этот закон распределения характерен для случайных погрешностей цифровых измерительных приборов, в которых измеряемая величина преобразуется в пропорциональный ей интервал времени Т_сч, называемый временем счета. Измерение этого интервала выполняется с помощью счетных импульсов стабильного генератора, имеющих заданный период следования Т_с. Положение счетных импульсов относительно интервала Т_сч является случайным, соотношение между Т_сч и Т_с является также случайным, следовательно максимальные погрешности этих величин равны, т.е. а₁=а₂ => закон распределения треугольный.

Рис.б) Подобным же образом формируется композиция равномерного и нормального распределений, только подъем и спад по краям результирующего распределения проходит по кривой интегрального закона нормального распределения.

Рис.в) Композиция равномерного с шириной а распределения и арксинусоидального с шириной в представляет собой криволинейную трапецию с верхним основанием а-в и нижним а+в и спадами по кривым интегрального закона аrcsin- распределения.

Рис.г) Композиция равномерного и распределения Лапласа (двустороннее экспоненциальное) имеет длинные, полого спадающие «хвосты» кривой результирующего распределения.

Реальный масштаб кривых на рисунках а-г определяется каждый раз тем, что площадь под любой из кривых плотности распределения должна быть равна 1.

Литература :

1. Вентцель А.Д. Курс лекций по случайным процессам. М., Наука, 1982.

2. Вентцель Е.С., Овчаров А.В. Прикладные задачи теории случайных процессов. М., Наука, 1992.

3. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов. М., Наука, 1972.