АВТОТРАНСПОРТНОЕ ПРЕДПРИЯТИЕ КАК МНОГОКАНАЛЬНАЯ СИСТЕМА С НЕОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ

Гарькина И.А., Карев М.Н.

Пензенский государственный университет архитектуры и строительства

Ниже автотранспортное предприятие рассматривается как n-канальная система с неограниченной очередью. Поток поступающих в систему заявок имеет интенсивность l, а поток обслуживаний – интенсивность m. Необходимо определить предельные вероятности состояний системы и показатели ее эффективности.

Система может находиться в одном из состояний S₀, S₁, S₂,...,S_k,..., S_n
(S₀ – заявок нет, каналы свободны, S₁ – занят один канал, остальные свободны, S₂ – заняты 2 канала, остальные свободны,... , S_n – заняты все каналы, а очереди нет, S_n+r – заняты все каналы, r заявок в очереди). Соответствующий граф приводится на рис.1.

Рис.1

Интенсивность потока обслуживания, переводящего систему из одного состояния в другое (справа налево), возрастает от m до nm по мере увеличения числа заявок от 0 до n (соответственно увеличивается число каналов обслуживания). При числе заявок, большем n, интенсивность потока обслуживаний сохраняется и равна nm. При < 1 предельные вероятности существуют. Если ³ 1, очередь растет до бесконечности. Предельные вероятности состояний n-канальной системы с неограниченной очередью определятся в виде:

,

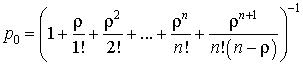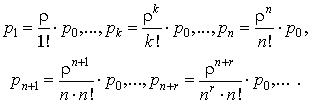
Легко показать:

– вероятность того, что заявка окажется в очереди P_оч;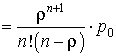

– среднее число занятых каналов ;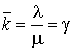

– среднее число заявок в очереди Z_оч,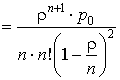

– среднее число заявок в системе Z=Z_оч+r.

Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе определятся по формулам Литтла. Для системы с неограниченной очередью при r < 1 любая заявка, пришедшая в систему, будет обслужена, то есть вероятность отказа =0. Относительная пропускная способность N=1, абсолютная пропускная способность равна интенсивности входящего потока заявок, то есть L=l.

В качестве иллюстрации рассмотрим работу билетной кассы автовокзала с интенсивностью потока пассажиров l=81 человек в час и средней продолжительностью обслуживания кассиром одного пассажира t_об=2 мин. С учетом l=81/60=1,35 (1/мин) имеем 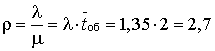. Очередь не будет возрастать до бесконечности при <1, то есть при Таким образом, минимальное количество кассиров n_min=3. Найдем характеристики обслуживания при n= n_min=3.

Вероятность того, что у кассы нет пассажиров

,

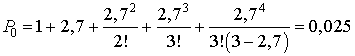то есть в среднем 2,5 % времени кассиры будут простаивать. Вероятность того, что у кассы будет очередь, равна:

P_оч=.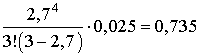

Среднее число пассажиров в очереди Z_оч=.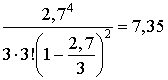

Среднее время ожидания в очереди T_оч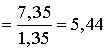 мин.

Среднее число покупателей у кассы Z=7,35+2,7=10,05.

Среднее время пребывания пассажиров у кассы .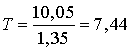

Среднее число кассиров, обслуживающих пассажиров, .

Доля занятых обслуживанием кассиров .

Абсолютная пропускная способность кассы L=1,35 (1/мин) или 81 пассажир в час.

Характеристики обслуживания при других значениях n приводятся в таблице

Характеристика обслуживания	Число кассиров n
	3	4	5	6	7
Вероятность простоя кассиров Р0	0,025	0,057	0,065	0,067	0,067
Среднее число покупателей в очереди Tоч	5,44	0,60	0,15	0,03	0,01
Относительная величина затрат Cотн	18,54	4,77	4,14	4,53	5,22

Минимальные затраты будут достигнуты при n=n_опт=5.