Педагогические науки/ 5. Современные методы преподавания

Канд. пед. наук, Школа О.В.

Національний педагогічний університет імені М.П. Драгоманова, Київ, Україна

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ДОВЕДЕННЯ ТА АНАЛІЗУ

ТЕОРЕМИ ЛІУВІЛЛЯ В СТАТИСТИЧНІЙ ТЕРМОДИНАМІЦІ

У розпорядженні викладача курсу теоретичної фізики сьогодні достатньо різноманітної навчально-методичної літератури як вітчизняних, так і зарубіжних авторів. Незважаючи на методичну цінність існуючих видань, необхідність удосконалення методики викладання навчального курсу за сучасних умов модернізації вищої педагогічної освіти в контексті європейських вимог, посилення уваги до якості фундаментальної і професійної підготовки майбутніх учителів фізики є цілком очевидною. З пасивного споживача знань студент має перетворитися на активного їх творця, оскільки справді фундаментальним є саме особистісне знання. Досвід засвідчує, що курс теоретичної фізики взагалі, а термодинаміки і статистичної фізики зокрема, є таким, що важко засвоюється, оскільки відрізняється високим рівнем формалізації основних понять, законів і теорій та відповідним рівнем математичного апарату. При цьому зменшення обсягу аудиторних годин, зміщення акцентів навчального навантаження студентів у бік самостійної роботи стають певними перешкодами на шляху якісного засвоєння основних/ключових питань навчального курсу. До числа останніх, зокрема, можна віднести й теорему Ліувілля про збереження фазового об’єму, яка відіграє важливу роль у класичній статистиці. У цьому контексті метою статті є короткий аналіз авторської методики доведення та аналізу фізичної сутності теореми Ліувілля в курсі термодинаміки і статистичної фізики, що має важливе професійно-педагогічне значення в підготовці майбутнього вчителя фізики.

Статистична фізика є одним з розділів теоретичної фізики, який вивчає специфічні властивості макроскопічних систем, що складаються з величезної кількості частинок (молекул, атомів, електронів, фотонів, фононів тощо). Саме велика кількість частинок призводить до появи нових закономірностей поведінки таких систем – статистичних законів, які мають імовірнісний характер, принципово не зводяться до динамічних законів і втрачають сенс при переході до систем з малим числом частинок.

Основане завдання статистичної теорії зводиться, по суті, до встановлення зв’язку між властивостями окремих частинок та параметрами, що характеризують макросистему в цілому. Для статистичної теорії є очевидним, що хаотичний рух частинок та взаємодія їх між собою і зовнішнім середовищем призводить до того, що як динамічні характеристики окремих частинок системи, так і її макропараметри у кожний момент часу мають випадкові значення. Тому для розв’язання основного завдання статистичної теорії необхідно ввести функцію розподілу за відповідними станами і в подальшому, на основі фізично обґрунтованих припущень, встановити явний вигляд цієї функції для різного класу макроскопічних систем [5, с. 120].

Для введення функції розподілу в статистичній фізиці, зазвичай, розглядається фазовий простір, у якому вимірами є три узагальнені координати та відповідні їм три узагальнені імпульси . Систему з частинок, таким чином, можна повністю описувати величинами. Кожна точка в такому просторі має координат і відображає певний мікроскопічний стан системи /її фазу/. Унаслідок теплового руху частинок значення та з часом змінюються, при цьому змінюються й мікроскопічні стани системи. У статистичній фізиці рух системи описують рівняннями Гамільтона:

; ; , (1)

де функція виступає механічною енергією системи.

Згідно статистичних уявлень Гіббса рух окремої частинки, як відомо, описують точними законами динаміки, проте через невизначеність початкових умов розрахувати стан досліджуваної системи для певного моменту часу ми не можемо, оскільки кожному її мікростану відповідає певна ймовірність. Тому замість однієї реальної можна розглядати деяке уявне число аналогічних систем (фазовий ансамбль систем), кожна з яких буде перебувати в одному з можливих для досліджуваної системи мікроскопічному стані. При цьому будемо користуватися основною гіпотезою про рівнорозподіл мікроскопічних станів системи, вважаючи, що остання може з однаковою ймовірністю потрапити до будь-якого елементарного об’єму фазового простору. Якщо кожній системі фазового ансамблю за допомогою певної функції розподілу приписати ту чи іншу ймовірність, то уявлення про фазовий ансамбль допоможе визначити термодинамічну ймовірність будь-якого макроскопічного стану досліджуваної системи. Такий фазовий ансамбль, де стан кожної системи характеризують певною ймовірністю, називають статистичним ансамблем Гіббса (САГ). Іншими словами, уявлення про фазовий простір та САГ безпосередньо приводить нас до статистики [3, с.23].

Системи, що складають САГ, можуть бути розподілені у фазовому просторі взагалі різноманітно. При цьому точки, що їх зображують, матимуть вигляд деякої об’ємної “багатомірної хмари”, межі якої взагалі можуть бути спрямовані у нескінченність. Число систем у будь-якому елементарному об’ємі фазового простору, очевидно, буде пропорційним величині цього об’єму: , де величина визначає розподіл систем у фазовому просторі (вона показує, яке число систем ансамблю /мікростанів/ припадає на одиницю фазового об’єму). Імовірність перебування однієї системи у фазовому об’ємі можна представити так:

, (2)

де - густина ймовірності /вона має зміст функції розподілу ймовірностей системи за її мікростанами/, знаходження якої виступає основним завданням статистичної фізики [1, с.21].

Однак перед встановленням загального вигляду функції розподілу , необхідно розглянути як змінюється з часом елемент фазового об’єму /це важливо з’ясувати, оскільки ймовірність перебування системи в елементі фазового об’єму пропорційна його величині, а останній зміщується та змінюється з часом/. Якщо досліджувана система є замкненою, тобто підпорядковується рівнянням Гамільтона (1), то виявляється, що число точок (мікростанів системи) в одиниці об’єму фазового простору під час руху лишатиметься сталим, тобто сукупність фазових точок поводить себе у фазовому просторі як “пружна рідина”. У цьому й полягає зміст так званої теореми Ліувілля про збереження фазового об’єму. На наш погляд, при викладенні основ статистичної фізики не можна задовольнятись лише доведенням цієї теореми, оскільки з неї під час аналізу можна одержати надзвичайно важливі результати, зокрема, про те, що всі можливі функції розподілу можна замінити єдиним розподілом – за енергією. Для того, щоб у цьому переконатись розглянемо один з можливих варіантів доведення та аналізу теореми Ліувілля [6, с.39].

Припустимо, що протягом тривалого часу ми спостерігаємо за системою, яка є малою часткою великої замкненої системи. Поділимо вказаний проміжок часу на малі однакові інтервали . У фазовому просторі системи відмітимо точки, які відповідають її станам у моменти, які відстоять на один від одного. Сукупність отриманих точок розподілиться у фазовому просторі з густиною, яка буде пропорційною в кожній точці значенню функції розподілу . Розглянемо поведінку сукупності фазових точок, які зображують ці системи ансамблю та перебувають у певному елементі об’єму фазового простору: . Унаслідок руху кожної точки за фазовою траєкторією форма цього елементу фазового простору з часом буде змінюватися взагалі довільно, проте його величина при цьому лишатиметься сталою. Докажемо цю теорему.

Сукупність фазових точок (систем ансамблю) з часом переходить з одного об’єму фазового простору в інший. Виділимо у будь-який момент часу об’єм , в якому буде перебувати згідно (2) систем ансамблю. Через деякий час ці системи переходять в об’єм з густиною розподілу . Тоді, очевидно, , оскільки маємо такі ж системи, які спочатку були в об’ємі , а потім змістилися в об’єм . Іншими словами, сукупність фазових точок не може виникати та зникати, також як не можуть виникати та зникати самі системи ансамблю. Ці міркування змушують нас розглядати “процеси втікання та витікання” фазових точок в об’єми як рух “фазової рідини”, до якого можна застосувати відоме рівняння безперервності у так званій диференціальній формі, яке являє собою закон збереження загального числа частинок (у даному випадку – фазових точок) статистичного ансамблю:

. (3)

Узагальнюючи операцію дивергенції на багатомірний -простір, отримаємо: [у нашому випадку ], де , а координати збігаються з узагальненими координатами та імпульсами системи. Похідні та виступають компонентами “вектору швидкості” фазових точок. Рівняння безперервності для газу фазових точок матиме вигляд: 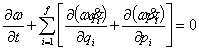. Продиференціюємо рівняння та згрупуємо члени:

.

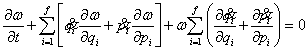Перші два доданки являють собою повний диференціал функції , тому останнє рівняння можна переписати: 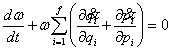. Згідно формули (1) для другого доданку маємо: . Отже, другий член у попередньому рівнянні обертається в нуль. Звідси отримаємо:

або . (4)

Рівняння (4) означає, що функція статистичного розподілу є сталою вздовж будь-якої фазової траєкторії у - просторі. Таким є зміст теореми Ліувілля. Враховуючи рівняння Гамільтона (1), формулу (4) можна переписати інакше: , де - скобки Пуассона [2, с.27]. Отже, для фазової густини ймовірності маємо рівняння Ліувілля:

. (5)

Формулу (5) використовують у вирішенні принципових питань статистичної теорії нерівноважних процесів, де з неї отримують спрощені рівняння з меншим числом незалежних змінних, які можна розрахувати практично. Проаналізуємо теорему Ліувілля більш детально.

1). Рівняння (4) означає, що під час руху вздовж фазової траєкторії густина числа фазових точок не змінюється. При цьому в різних місцях фазового простору густина розподілу точок може різнитися і змінюватися з часом, тобто взагалі . Однак з (4) виходить, що повної зміни з часом не відбувається, тобто . Зазначимо, що для ізольованої системи у стані термодинамічної рівноваги згідно (4) всі мікростани, що належать фазовій траєкторії, рівноймовірні.

2). Оскільки число фазових точок під час руху у фазовому просторі завжди зберігається, маємо: . Згідно (4) , звідки виходить, що . Цей результат можна сформулювати як принцип збереження елементарного фазового об’єму (за Гіббсом): під час руху точок у фазовому просторі елементарні об’єми лишаються сталими і можуть змінюватися тільки за формою, тобто деформуватися, зберігаючи при цьому свою величину. Аналогічним чином рухається з місця на місце бджоляний рій. Отже, сукупність фазових точок поводить себе у фазовому просторі як “пружна рідина”, іншими словами, “газ фазових точок” стиснути неможливо.

3). Якщо для будь-якого моменту часу ймовірність перебування фазової точки (системи ансамблю) у певному елементі об’єму простору відома, то вона буде відомою і для будь-якого іншого моменту. Унаслідок цього стає можливим замість початкових умов, які використовують в механіці, прийняти статистичне припущення Больцмана про рівноймовірність всіх станів системи, які зображуються елементами (клітинками) фазового простору рівного об’єму.

За допомогою теореми Ліувілля можна доказати попереднє припущення про пропорційність числа систем (точок) у певному фазовому об’ємі величині цього об’єму. Якщо б величина фазового об’єму не зберігалася, говорити про пропорційність ймовірності перебування системи у певному об’ємі його величині не можна. Але, оскільки, сталість фазового об’єму та густини тепер доказана, то завжди чим більший фазовий об’єм обираємо за умов сталої густині, тим більше число систем у ньому буде перебувати.

4). Згідно (4) повний диференціал густини розподілу фазових точок завжди дорівнює нулю, хоча частинна похідна взагалі різниться від нуля. Розглянемо тепер окремий випадок, коли , який відповідає стаціонарному рухові фазових точок: скільки точок входить до даного фазового об’єму за одиницю часу, стільки ж з нього виходить. Очевидно, ця умова відповідає рівноважному стану систем ансамблю, тому можна говорити, що ансамбль перебуває у стані статистичної рівноваги, коли фазова густина скрізь не залежить від часу. У статистичній фізиці розглядаються саме такі системи. Отже, умова виступає одночасно й самою загальною умовою статистичної рівноваги. Густина розподілу в цьому випадку є функцією тільки координат фазового простору: .

5). Якщо , то згідно виразу (4) виходить: 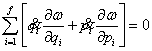. З урахуванням рівнянь (1), маємо: 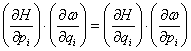. Функція Гамільтона виступає інтегралом руху, тобто величиною, яка з часом не змінюється. Густина розподілу систем ансамблю за умов статистичної рівноваги також не залежить від часу, тобто теж виступає інтегралом руху. Можна припустити, що залежить тільки від . З останнього рівняння видно, що таке припущення можливе. Дійсно, якщо , маємо співвідношення:

.

Отримане рівняння є справедливим для будь-якої диференційованої функції . Таким чином, зроблене припущення є законним. Це дає можливість вирішувати в загальному випадку основне завдання фізичної статистики, тобто знаходити розподіл систем за енергіями. Отже, густина розподілу систем не залежить від часу, вона залежить лише від енергії системи ; зміна величини фазового об’єму при цьому виключається. Все це змушує припустити, що для макросистем, які перебувають у стані статистичної рівноваги, існує деякий універсальний розподіл за енергіями. Дж.Гіббс знайшов цей розподіл у 1901 р. і назвав його канонічним.

Підсумовуючи, зазначимо, що багаторічний досвід викладання автором курсу термодинаміки і статистичної фізики в педагогічному університеті підтверджує ефективність пропонованої методики доведення й аналізу теореми Ліувілля, про що свідчать високі навчальні результати студентів з розв’язування відповідних задач на практичних заняттях, так і під час підсумкового модульного контролю.

Література:

1. Ансельм А. И. Основы статистической физики и термодинамики / А. И. Ансельм. – М. : Просвещение, 1973. – 423 с.

2. Венгер Є. Ф. Основи статистичної фізики і термодинаміки / Є. Ф. Венгер. – К. : Вища школа, 2004. – 255 с.

3. Гиббс Дж. Термодинамика. Статистическая механика / Дж. Гиббс ; отв. ред. Д. Н. Зубарев. – М. : Наука, 1982. – 584 с.

4. Королюк С.Л. Основи статистичної фізики та термодинаміки / С. Л. Королюк, С. В. Мельничук, О.Д. Валь. – Чернівці : Книги ХХІ, 2004. – 347 с.

5. Мороз І. О. Теоретико-методичні засади вивчення термодинаміки і статистичної фізики в педагогічних університетах : монографія / І. О. Мороз. – Харків : ТОВ “Діса плюс”, 2012. – 382 с.

6. Школа О. В. Основи термодинаміки і статистичної фізики : навч. посібник / О. В. Школа. – Донецьк : Юго-Восток, 2009. – 374 с.