Васильев Иван
Анатольевич
Санкт-Петербург, ЦНИИ
РТК, нач. лаб., к.т.н
Шагающий мобильный робот: траектории движения стопы
В предыдущих статьях описывалась решение обратной
кинематической задачи и решение проблем с конфигурацией подстилающей
поверхности. Теперь рассмотрим траекторию движения стопы в цикле шагания. Как
было сказано выше, для комфортного движения удобно считать маятник двигающимся
свободно. Поэтому в режиме опоры нога не сможет обеспечить прямолинейное
движение «стопы». Пусть на этом этапе движение происходит по эллиптической
траектории – нелинейность можно будет компенсировать шарниром качания «таза».
На рисунке 1 показана траектория движения «стопы» без учёта компенсации «таза».
Так как в момент контакта с опорной поверхностью нога предполагается
выпрямленной (т.е. расстояние от шарнира качания «бедра» до стопы равно a+b+c),
то требуется, чтобы эта прямая пересекалась с требуемой траекторий «стопы» как
касательная.
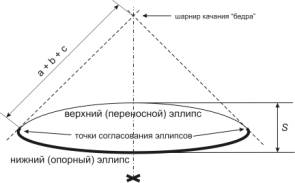
Рис. 1. Траектория
движения стопы
Угловой коэффициент касательной к эллипсу, заданному
параметрически, как известно, выглядит так:
где r и R – малый и большой
радиусы эллипса,
– угловой параметр
эллипса.
Следовательно, можно составить систему уравнений:
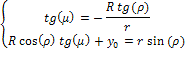
где 
– угловой
коэффициент касательной;
а второе уравнение это касательная к эллипсу.
Подставляя первое уравнение во второе и упрощая, получаем
решение:
Шаг характеризуется двумя параметрами: длина и высота. Если
длину мы учитываем как двойной радиус нижнего (опорного) эллипса (рис. 1), то
высоту шага (на рис. 1 обозначена S)
надо задавать в уравнениях, в которых согласуются два эллипса.
Здесь надо вспомнить, что в точках согласования касательные
к обоим эллипсам проходят через шарнир качания «бедра», что резко упрощает
нахождение решения.
Итак, найдём сначала касательную к эллипсу, проходящую через
точку (0, у0). Напишем уравнение точки пересечения прямой (
) и эллипса (
) :
где 
угловой коэффициент прямой;
ордината шарнира.
Угловой коэффициент касательной равен производной в точке
касания:
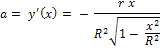
Отсюда получаем решение для двух точек касания:
(2)
Если пытаться находить верхний эллипс как совпадающий с
нижним эллипсом по производным в точках касания, то получаются решения
циклопических размеров. Поэтому произведём операцию, обратную вышеприведённой:
найдём эллипс, который имеет те же касательные и проходит через точку А (см.
рисунок 1).
Из этих соображений получаем три уравнения и три
неизвестных: оба радиуса и смещение эллипса по вертикали:
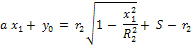
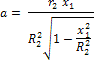
где 
– параметры
касательной прямой;
- радиусы верхнего
эллипса;
- смещение верхнего
эллипса по ординате;
– точка пересечения
эллипсов (найдена в формуле (2)).
Отсюда находим параметры верхнего эллипса:
Здесь горизонтальный радиус эллипса получается автоматически
верным, так как смещение по оси ординат (
) нами определено, а смещение по абсциссе – нет.
Следовательно, и верхний эллипс симметричен относительно оси ординат.
Заключение.
В заключение можно сказать, что многоногий шагающий робот
планируется разработать в ближайшее время и на нём будут использованы идеи,
приведённые в данной статье. Так как мобильные транспортные средства имеют
ограниченную энерговооружённость, то оптимизация энергетических расходов на
движение механизмов движителя является определяющей.
Дальнейшие исследования предполагают произвести динамический
расчёт шагающего движителя.
Литература
1.
И.А. Васильев, А.М. Ляшин.
Классификация и аналитическое решение обратной кинематической задачи для
шестизвенных манипуляторов. // «Искусственный интеллект», №3 – 2004;
2.
I.Vasilyev, A.Lyashin. Classification and analytical solution for
inverse kinematical problem for 6-DOF manipulators. // Труды конференции
«Mechatronics & Robotics ‘04» Aachen – Germany, 2004
3.
В.В. Белецкий. Двуногая ходьба. М.,
«Наука» - 1984.
4.
В.М. Зациорский, А.С. Аруин, В.Н.
Селуянов. Биомеханика двигательного аппарата человека. М., «Физкультура и
спорт» - 1981
5. В.П. Воробьев. Атлас анатомии человека. Т. 1. М., МедГИз – 1938.