Математическая модель динамики тоннеля глубокого заложения, подкрепленного двухслойной обделкой, при транспортных нагрузках

Технические науки/2. Механика

К.т.н. Гирнис С.Р., д.т.н. Украинец В.Н.,

Павлодарский государственный университет, Казахстан

Изучение динамики тоннелей при действии транспортных нагрузок (нагрузок от движущегося внутритоннельного транспорта) методом математического моделирования приводит к краевым задачам механики деформируемого твердого тела. Как показывают расчеты [1], с увеличением глубины заложения тоннеля эффект динамического воздействия транспортной нагрузки на земную поверхность снижается, и при глубине около четырёх его характерных поперечных размеров становится несущественным. В этом случае при решении транспортной задачи земную поверхность можно не учитывать и рассматривать сооружение как тоннель глубокого заложения (заглубленный тоннель). С библиографий, касающейся математического моделирования таких тоннелей при различных нагрузках и воздействиях, можно ознакомиться в монографиях [1,2]. Впервые модельная для заглубленного тоннеля транспортная задача о действии движущейся осесимметричной нормальной нагрузки на однородную цилиндрическую оболочку в упругой среде рассматривалась в работе В.М. Львовского, В.И. Онищенко, В.И. Пожуева [3]. Аналогичные исследования для двухслойной оболочки (с тонким внутренним и толстым наружным слоями) проведены в [4]. В настоящей работе построена математическая модель динамики заглубленного тоннеля, подкрепленного двухслойной круговой обделкой с толстым внутренним и тонким наружным слоями, под воздействием транспортной нагрузки.

В качестве расчетной схемы тоннеля рассмотрим бесконечно длинную круговую цилиндрическую полость радиусом , расположенную в линейно-упругом, однородном и изотропном пространстве. Полость подкреплена двухслойной оболочкой, наружным слоем которой является тонкостенная оболочка толщиной , а внутренним – толстостенная оболочка с радиусом внутренней поверхности . В силу малости толщины наружного слоя можно принять, что он контактирует с толстым слоем и окружающим массивом вдоль своей срединной поверхности. Контакт между слоями оболочки, а также контакт между оболочкой и окружающим её массивом будем полагать либо жёстким, либо скользящим при двусторонней связи в радиальном направлении. Условимся внутренний слой оболочки называть несущим слоем, а наружный – ограждающим слоем. По внутренней поверхности оболочки в направлении ее оси с постоянной скоростью (меньшей, чем скорости распространения волн сдвига в несущем слое и массиве) движется нагрузка .

Так как рассматривается установившийся процесс, то картина деформаций стационарна по отношению к движущейся нагрузке. Поэтому для решения задачи можно ввести подвижную цилиндрическую систему координат , связанную с нагрузкой.

Для описания движения ограждающего слоя воспользуемся классическими уравнениями теории тонких оболочек

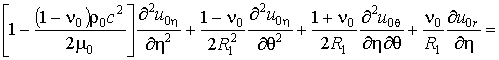
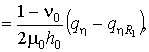
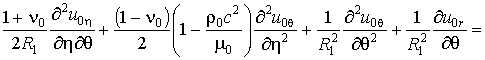
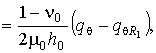(1)

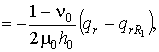
где , , – перемещения точек срединной поверхности ограждающего слоя в направлении осей цилиндрической системы координат , , ; , – составляющие реакции несущего слоя и массива (j = h, q, r); , – компоненты тензора напряжений в несущем слое и массиве; – соответственно коэффициент Пуассона, модуль сдвига и плотность материала ограждающего слоя; – оператор Лапласа.

Для описания движения несущего слоя и массива используем динамические уравнения теории упругости

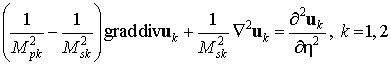. (2)

Здесь и в дальнейшем индекс k=1 относится к массиву, а k=2 – к несущему слою; – числа Маха; , – скорости распространения волн расширения – сжатия и сдвига в массиве и несущем слое; , – модули сдвига, – коэффициенты Пуассона, – плотности, – векторы смещений точек массива и несущего слоя.

Выражая векторы смещений через потенциалы Ламе

, (3)

преобразуем уравнения (2) к виду

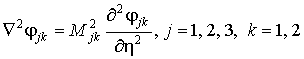, (4)

где .

Выразим компоненты напряжённо-деформированного состояния (НДС) массива и несущего слоя через потенциалы j_jk.

Компоненты вектора u_k (3):

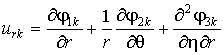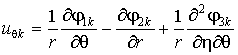, (5)

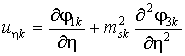где .

Используя закон Гука и соотношения (5), получаем выражения для компонент тензора напряжений

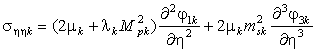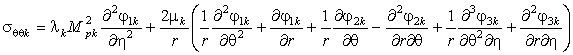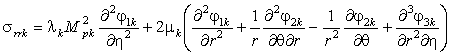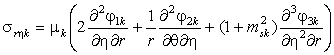, (6)

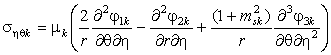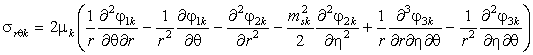Применив к (4) преобразование Фурье по , находим

, (7)

где – двумерный оператор Лапласа, , .

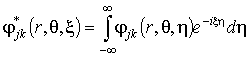Применив к (5), (6) преобразование Фурье по , можно получить выражения для трансформант перемещений и напряжений () в цилиндрической системе координат как функции от .

Так как скорость движения нагрузки меньше, чем скорости распространения волн сдвига в несущем слое и массиве, то , и решения (7) можно представить в виде:

- для массива

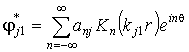, (8,а)

- для несущего слоя

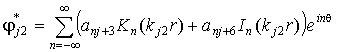. (8,б)

Здесь , ; – функции Бесселя первого и второго рода от мнимого аргумента, – неизвестные коэффициенты, подлежащие определению.

Подставляя (8,а), (8,б) в выражения для трансформант перемещений и напряжений , можно получить новые выражения для и с неизвестными коэффициентами , для определения которых следует воспользоваться граничными условиями.

Применив к (1) преобразование Фурье по и разлагая функции перемещений точек срединной поверхности ограждающего слоя в ряды Фурье по , для -го члена разложения получим

(9)

где

;

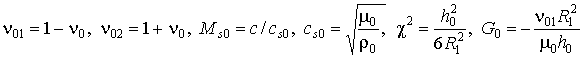, , ; – коэффициенты разложения в ряды Фурье по угловой координате .

Разрешая (9) относительно , , , находим

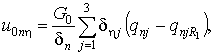
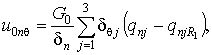(10)

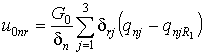Здесь

для q_nj и индекс j = 1 соответствует индексу h, j = 2 – q, j = 3 – r.

Граничные условия можно представить в следующем виде:

а) при жестком сопряжении слоев оболочки:

- в случае скользящего контакта оболочки с массивом

при , , , ,

при , ,

- в случае жёсткого контакта оболочки с массивом

при , ,

при , ;

б) при скользящем контакте слоев оболочки:

- в случае скользящего контакта оболочки с массивом

при , , , , , ,

при , ,

- в случае жёсткого контакта оболочки с массивом

при , , , ,

при , .

Здесь , .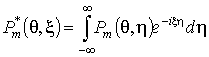

Разлагая в ряды Фурье по угловой координате q и приравнивания коэффициенты рядов при , получим бесконечную систему линейных алгебраических уравнений для определения коэффициентов. После определения коэффициентов , применяя обратное преобразование Фурье, можно вычислить компоненты напряженно-деформированного состояния массива и оболочки. При этом для вычисления интегралов Фурье можно использовать любой численный метод, если определитель полученной для конкретных граничных условий системы уравнений не обращается в ноль. В общем случае для любых аналитическое исследование затруднительно. Численные исследования в задачах о движущейся вдоль оси подкреплённой полости осесимметричной нормальной нагрузке в упругом пространстве [4] показали, что может существовать дозвуковая критическая скорость , при которой в двух точках

При существуют четыре особые точки , в которых

В этих случаях, как доказано в [4], нарушены условия единственности решения, что можно трактовать как неустойчивость. При переходе через появляется класс решений, содержащий незатухающие гармонические поверхностные волны. Амплитуда этих волн зависит от действующей нагрузки, постоянна вдоль оси и экспоненциально затухает при .

При для любых . В этом случае допустимо прямое и обратное преобразование Фурье и полученные соотношения решают поставленную задачу.

Литература:

1. Украинец В.Н. Динамика тоннелей и трубопроводов мелкого заложения под воздействием подвижных нагрузок. – Павлодар: НИЦ ПГУ им. С. Торайгырова, 2006. – 123 с.

2. Ержанов Ж.С., Айталиев Ш.М., Алексеева Л.А. Динамика тоннелей и подземных трубопроводов. – Алма-Ата: Наука, 1989. – 240 с.

3. Львовский В.М., Онищенко В.И., Пожуев В.И. Установившиеся колебания цилиндрической оболочки в упругой среде под действием подвижной нагрузки //Сб.: Вопросы прочности пластичности. – Днепропетровск, 1974. – С. 98-110.

4. Алексеева Л.А., Украинец В.Н. критическая скорость движущейся нагрузки в тоннеле, подкрепленном двухслойной оболочкой//Изв. АН СССР. Механика твердого тела. – 1987. – № 4. – С.156-161.

Работа выполнена при поддержке гранта 0898/ГФ2, 0112РК02221 МОН РК.