Технические науки/2. Механика

D.tech.scien. Artamonova E.N., Grigorieva E.V.

Saratov State Technical University n.a. Gagarin Y.A., Russia

Modeling of destruction of polymeric materials

In this paper we propose a mathematical model of destruction (the relations connecting parameters of efficiency at the time of fracture characteristics material), based on the relationship of both these approaches to allow for the dependence of the limiting critical conditions at which the destruction, the time of stress, temperature environmental exposure, exposure, etc. This is especially typical for polymers [1]. An examination of these experimental data one can draw conclusions that should be taken into account when constructing the mathematical correlations for the conditions of fracture:

Mechanical properties and the process of destruction of polymer materials substantially depend on time and operating conditions.

Destruction is a two-stage process. At the first stage the degradation of the properties of the material, the accumulation of damage, microcracks occur. The stage ends at a time when the merger of microdamage formed macroscopic crack. This moment is short-lived and by their physical nature is a loss of stability of equilibrium microdefects.

Because of the irreversibility of the process of destruction is determined not only the current values of parameters characterizing it, but the entire prior history change of these parameters.

Because of the private nature of the experimental data on the effect of medium on behavior of plastic the composition of the general mathematical for all materials the phenomenological description of fracture based on mechanical ideas due to the difficulties and serious shortcomings. Therefore it is necessary and the molecular interpretation of macroscopic changes in the material. Thus, the phenomenological theory of time dependence as would provide a common framework, which must fit the theory of material behavior, and that put a detailed mechanical theory of change of macroscopic and microscopic properties of the polymer. This need arises in the interpretation of the parameters of the phenomenological equation, allowing you to identify not only the common features, as well as the difference between the materials.

Because of significant time effects for polymers the process of their destruction more difficult than traditional materials, the phenomenon of viscous and brittle fracture occur simultaneously. Fracture criterion in this case must take into account the achievement σ, ε of the instantaneous and destructive values σ р, ε р, at the time tразр., and their dependence on the development of degradation of material properties ω (t).

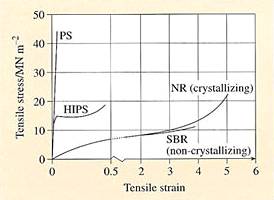
Figure 1.

Analysis of experimental data (Fig.1) suggests characteristics of the temperature dependence of relaxation processes and fracture for viscoelastic polymers with the same value of energy activation for each material.Both aspects of the strength of polymers depend on the local structural changes that primarily can be linked with the process of accumulation of damage, education grid hairline cracks. Combining different approaches to describing these processes, i.e. formulation of a general mathematical theory of deformation and fracture of polymers depends on the study of the relationship of deformation, destruction and action of strain, temperature, aggressive factors in the whole time interval of operation of the element.

According the survey of the literary sources for the analyzing of long-term durability of materials and elements made of them two alternative approaches are basically exist: mechanical (benchmarking) and kinetic.

According the first approach we model the generalized condition for material destroying:

Ф (θ1, θ2, θ3 ) = Ф р.

Here Ф - the functional is some combination of the components of the stress or strain. The functional Ф depends on the accepted theory strength or given empirically and then the functional contains parameters determined experimentally.

Ф = ∫dV [1/2 ρu iu i– λ/2 ∂ui/∂xi ∂uj/∂xj - µ/2( ∂ui/∂xj ∂ui/∂xj + ∂ui/∂xj ∂uj/∂xj)].

1.The strain tensor can be represented as a sum of tensors of elastic deformation of inelastic deformation:

ε ij = ε ij¹ + ε ij².

2. For description the strain state and fracture in the framework of a generalized model of inelasticity is necessary to consider the history of deformation of the sample depends on the loading path and on time. For different loading paths for the processes of varying duration results will be different.We give a physical explanation of the above stated hypothesis.

References:

1. Suvorova J.V., Ohlson N.G., Alexeeva S.I. An approach to the description of time-dependent materials //Materials and Design, Vol.24. Issue 4, June 2003.- P.293-297.