Комолов В.М.,  канд. физ.-мат.  наук  Латынин Ю.М.

Украинская инженерно-педагогическая академия. г. Харьков

 

Кривые Персея: геометрическая структура

 

Введение. Кривые Персея − алгебраические линии 4-го порядка. Они являются линиями пересечения поверхности тора плоскостями, параллельными его оси. В декартовой системе координат уравнение, которое описывает эти кривые, имеет вид [1,2]:

                                                   (1)

где R − радиус производящей окружности тора; d − расстояние центра производящей окружности от начала координат; p − расстояние секущей плоскости от начала координат; (х,у) − система координат в секущей плоскости.

Уравнения, описывающие кривые Персея, при планиметрическом способе получения и системе координат (х,у) имеют следующий вид [1]:

              .             (2)

Здесь точки F(m,0), F1(-m,0) − фокусы кривых Персея, с,с1 − заданные константы.  Из (2) при с=0 получают овалы (линии) Кассини; при с= 0 и  с1= m4 −  лемнискату Бернулли, при с1= m4 –лемнискату Бута.

Рис.5. Дельтоида

 
 

Представление различных типов кривых в комплексной форме позволяет вскрыть их внутреннюю структуру, установить взаимосвязь между ними

Основная часть. I. Овалы (линии) Кассини.

Произведем  в (2)  стандартные переобозначения: с1= а4  и с=0, получим:

               .                              (3)

  В полярных координатах:

         .               (4)

Форма кривых зависит от отношения а/m. Рассмотрим случай, когда а>m. Введем обозначение          a2/m2 = ch(2η), т.к  a/m>1 , a4/m4 −1 =sh2(2η).        (5)

Тогда .             (6)

Так как           , то

         ,                                    (7)

причем, поскольку  а>m, то в (4), (7) берется только знак (+). Учитывая, что       . Далее используем формулу, которая является аналогом соответствующего  соотношения в теории функций комплексного переменного.

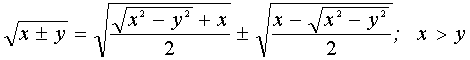                            (8)

Т.к.                 

Примем                                             (9)

Тогда          

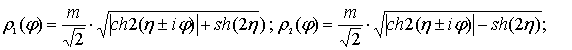     (10)

Таким образом, в полярной системе координат при a≥m  каждый овал Касссини представляет собой суперпозицию двух замкнутых кривых, являющихся обобщенными четырехлепестковыми розами [3]. Оси декартовых координат служат осями симметрии этих кривых. Исследуем их поведение.

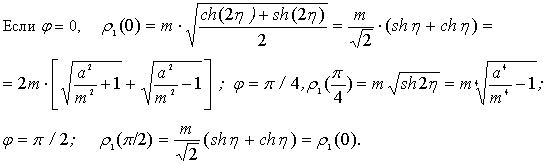 (11)

Аналогично, для тех же углов ρ2:

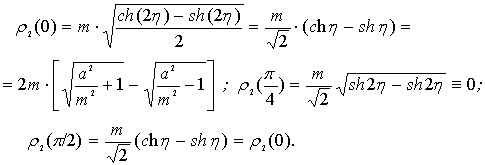               (12)

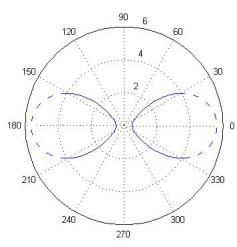
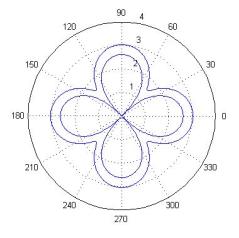
Анализ показывает: семейство роз, описываемых соотношением ρ1=ρ1(φ) при росте параметра a/m (a>m) увеличивается в размерах, а семейство роз, описываемых ρ2=ρ2(φ) – наоборот неограниченно убывает (см. рис. 1,2). Для интервалов углов  -π/4 ≤φ≤ π/4 и (3/4)π ≤φ≤ (5/4)·π   линия Кассини описывается суммой                                                              (13)

В  интервале углов   π/4 ≤ φ ≤ (3/4)·π и (5/4)π ≤ φ ≤ (7/4)·π   линиям Кассини соответствует разность                                     (14)

Рис.1

Рис.2

 

 

 

 

 

 

 

 

 

II. Лемниската Бернулли.  Полагая в (2) с=0, c1= m4 , получают уравнение кривой  в виде:

                                                                     (15)

При этом отношение величин а/m = 1, (sh(2η)=0)  и в полярной системе координат                      (16)

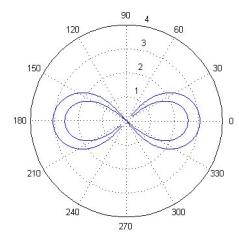
Угол   φ  изменяется в пределах  -π/4≤φ≤ π/4 , (3/4)π≤φ≤(5/4)π; лемниската Бернулли есть частный случай овала Кассини и ее также можно отнести к группе обобщенных роз [3]. Как следует из (10) при   а/m=1.

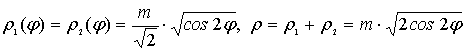                            (17)

При а/m→1, составляющие овалов Кассини ρ1, ρ2 сближаются и в пределе совпадают, образуя лемнискату Бернулли.

III. Овалы Кассини, а<m. Примем как и в [1] a2/m2 = sin(2α). Тогда уравнение (4) можно записать в виде

                                                 (18)

Так как  a < m, то sin(2α) <1 и  α < π/4. Из (18) следует, что при изменении угла φ от 0 до α каждому его значению будет соответствовать два действительных значения ρ±(φ):

    .                               (19)

  При φ=0                                           (20)

При  возрастании φ от 0 до α    убывает, а − наоборот, возрастает.

Рис.3 

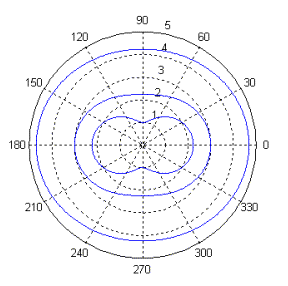
При φ=α == т.е овал Кассини состоит из двух замкнутых линий − овалов, каждый из которых находится внутри лепестка лемнискаты Бернулли (рис. 3). Будем называть этот тип линий − «малый» овал.

Покажем, что каждый «малый» овал имеет внутреннюю структуру. С этой целью снова используем (8) для преобразования (19). В этом случае

                          (21)

Тогда    ;   где          (22)

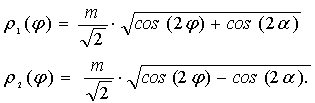                                                          (23)

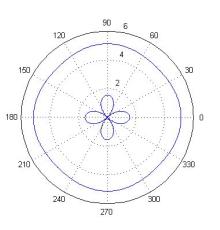
Из анализа этих кривых вытекает, что каждая из них есть лепесток обобщенной розы с несовпадающим угловым раскрывом. «Малый» овал ρ1 имеет угол раскрыва (π − 2α), второй ρ2 − угол раскрыва 2α. На рис. 4  изображены кривые составляющих    ρ1 ,  ρ2  , когда  2α=80 º.

Также установлено, что каждый «малый» овал состоит из двух отрезков дуг. Крайняя (удаленная от центра) часть овала равна:

                                           (24)

Другая часть овала, расположенная ближе к началу координат, равна

                                              (25)

Рис.4. ρ1(φ) – внешний лепесток,  

     ρ2(φ) – внутренний лепесток

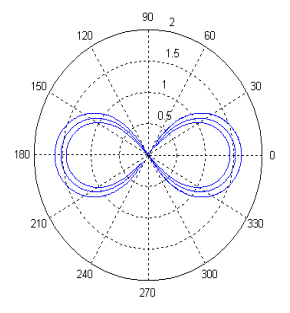
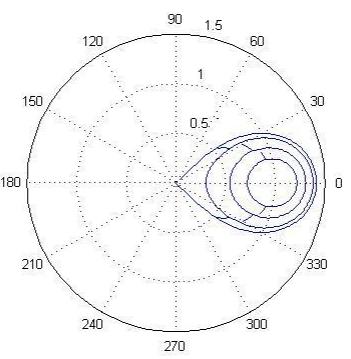
Рис.5. --- ρ1(φ)+ ρ2 (φ);         

           —ρ1(φ)−ρ2 (φ)

 

 

 

 

 

 

 

 

 

 

При φ=±α  одна дуга кривой переходит в другую, при этом  ρ1=mcos(2α) и ρ2 =0 (см. графики рис.5, где изображены кривые «малых» овалов). Таким образом, лемниската Бернулли есть граничная кривая, которая разделяет две области, в каждой из которых имеется отличная от другой внутренняя структура. Общим является то, что основу каждой структуры составляют обобщенные розы [3].

IV. Бута лемниската – плоская алгебраическая кривая 4-го порядка. Ее уравнение в декартовой системе координат совпадает с (2) при с1 = m4:

                                 (26)

H:\But2.bmp

Рис.6  Эллиптический тип  

        лемнискаты Бута

         H:\But4.bmp

                   Рис.7. Гиперболический тип

                             лемнискаты Бута

 

Здесь также m>0 − фокусное расстояние лемнискаты Бута, с − заданная константа. Различают эллиптическую и гиперболическую  лемнискаты Бута.

Эллиптический тип характеризуется наличием изолированной особой точки в начале координат, гиперболический − имеет в начале координат узловую точку (см. рис.6,7). Рассмотрим каждый тип лемнискаты Бута отдельно.

Эллиптический тип: c >2m2 . В полярной системе координат из (26)

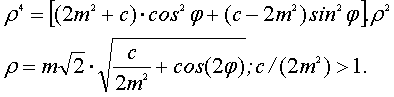                                 (27)

Обозначим  c/(2m2)=ch(2u).       Тогда:

                 (28)

Это есть замкнутая кривая, оси координат являются осями симметрии. При φ=0

                

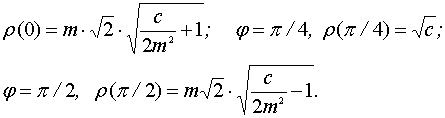
Гиперболический тип: с < (2m2) . Из (26)

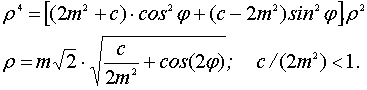                                       (29)

 Обозначим  с/(2m2 ) = cos(2α).          Тогда:

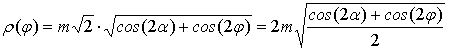                            (30)

Эта кривая может быть отнесена к обобщенной двухлепестковой розе, причем угол раскрыва каждого лепестка  равен (π−2α). Следует также указать, что кривая, описываемая уравнением (30), с точностью до постоянного множителя совпадает с одной из составляющих кривых «малого» овала, а именно ρ1(φ) - (23). Таким образом, лемниската Бута гиперболического типа является составляющей овалов Кассини.

Выводы:  Кривые Персея (овалы Кассини, лемнискаты Бута и Бернулли,) имеют внутреннюю геометрическую структуру, основу которой составляет суперпозиция обобщенных роз.

Список литературы:

1. Савелов А.А. Плоские кривые. Систематика, свойства, применения. Справочн. руководство. - М.: Гос изд. физ.-мат литературы, 1960.- 294 с.

2. Математическая энциклопедия: гл. ред. И.М. Виноградов, М.: Советская энциклопедия, 1984, т.1-5.

3. Комолов В.М., Латынин Ю.М. Розы  как составляющие трохоидальных кривых. Materials of the X1 International scientific and practical сonference «Modern european science,-2015», Vol.9, Mathematics, Physics…, Sheffield. Science and Education LTD.- P.32-38