Математика/5. Математическое моделирование

Пряжнікова К.В., к.э.н. Бєлкіна І.А.

Національний гірничий університет, Україна

Моделювання динаміки надходження руди на збагачувальну фабрику

Доставка руд з кар’єру на дробарно-збагачувальний переділ відбувається безперервно. Але цей процес має імпульсний періодичний характер, який пояснюється організацію доставки сировини залізничним транспортом. Відповідно до існуючої організації виробничого процесу на гірничо-збагачувальних комбінатах, у вигляді імпульсного процесу можна представити транспортування руди не лише з кар’єрного складу на дробарну фабрику, але і переміщення її між будь-якими іншими ланками виробництва.

Кожен залізничний состав безперервно циркулює по ланках «кар’єр-дробарна фабрика». Тому процес відвантаження руди одним, виділеним залізничним составом має свій період та тривалість. Період надходження руди дорівнює T і визначається довжиною і станом залізничних шляхів, а також технічними характеристиками транспортного та навантажувального обладнання.

На Рис. 1.1 схематично зображено імпульсну функцію подачі руди на дробарну фабрику.

Q(t)

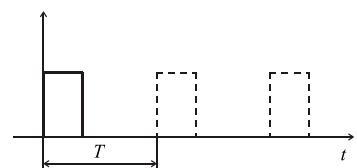
Рис. 1 – Імпульсна функція подачі руди на збагачувальну фабрику

Розглянемо більш докладно одиничну поставку руди на дробарну фабрику. За допомогою коефіцієнтів комплексного ряду Фурье знаходимо значення n-ної амплітуди спектра, згідно до номеру поставки руди [1]:

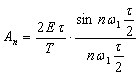, (1)

де Е – амплітуда прямокутних імпульсів;

τ – тривалість імпульсу;

Т – період функції;

У рамках даного дослідження будемо розглядати дробарну фабрику як аперіодичну стійку ланку з запізненням, тож згідно з [2] передаточна функція і АЧХ дробарної фабрики матимуть наступний вигляд:

(2)

(3)

де p – оператор Лапласа;

t₁ – постійна часу;

t₃ – період запізнення початку перехідного процесу;

k₁, k₂ – коефіцієнти перетворення відповідно для аперіодичної складової і складової запізнення.

Відповідно до роботи [3], передаточна функція і АЧХ для бункера матимуть вигляд:

, (4)

, (5)

де T_б – постійна часу бункера.

Гірничо-збагачувальний комбінат слід розглядати як систему, яка складається з послідовно з’єднаних ланок: кар’єру, дробарної фабрики, бункеру та збагачувальної фабрики. Згідно до теорії автоматичного керування [4] передаточна функція послідовно з’єднаних ланок дорівнює добутку передаточних функцій окремих ланок:

(6)

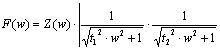(7)

За допомогою зворотнього перетворення Фурье знаходимо функцію часу f(t) з комплексної функції частоти F(w):

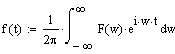(8)

Кількість руди R, що проходить через дробарну фабрику та бункер може бути розрахована, як визначений інтеграл функції f(t). Графічно ж представляє собою площу фігури, зображеної на графіку:

(9)

Функція часу f(t) показує динаміку надходження однієї поставки руди на збагачувальну фабрику, що дає змогу керувати надходженням кількості руди в момент часу.

Література

1. А. Анго Математика для электро- и радиоинженеров М., 1965г. 780 с.

2. Справочник по обогащению руд. Подготовительные процессы / Под ред. О.С. Богданова, В.А. Олевского. – М.: Недра, 1982. – 366 с.

3. Потапов В.Д. Имитационное моделирование производстввенных процессов в горной промышленности / В.Д. Потапов, А.Д. Яризов. – М.: Высшая школа, 1981. – 191 с.

4. Іванов А.О. Теорія автоматичного керування: Підручник/ А.О.Іванов. – Дніпропетровськ: НГУ, 2003. – 250с.