УДК 532:536.24;533.9

Божанов Е.Т., Ибраимкулов А.М., Касымбекова М.Т.

Казахский Национальный Технический Университет имени К.И.Сатпаева, Казахстан, Алматы

Математическая модель расчета выпучивания тонкостенной многослойной конструкции под действием ударного импульса, присдвиговом деформировании площади контакта, когда сила контактного воздействия сосредоточенная под нагрузкой, о конструкция закреплена

Постановка задачи

В качестве мишени рассмотрим тонкостенную многослойную конструкцию длиной – L, толщиной – h, шириной – b, с переменными параметрами поперечного сечения, лежащую на обобщенном упругом основании типа Коссера ([1] – [2]).

Пусть на поверхность в конструкции действует критический импульс в виде неравномерной поперечной силы произвольной эпюры. При этом размеры площадии контакта взаимодействующих тел и форма критический деформации зависит от эпюры неравномерной поперечной силы.

Ударный импульс производится в центре плоскости мишени в начале координатной системы, в зоне контакта происходят относительные удлинения, смещения деформации.

Матемтическую модель взаимодействующих тел в зависимости дифференциального уравнения изгиба серединной оси поперечного сечения возьмем в виде [3] – [4]:

(1) (1)

Сделаем замену переменной

(2) (2)

подставляя (2) в (1) получим:

(3)

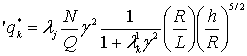
Общее решение (3) представляется в виде

(4)

Где – какое-нибудь частное решение дифференциального уравнения (3), которое очень легко определяется в зависимости от вида правой части.

– общее решение однородного уравнения.

(5)

Так как коэффициент 2В – намного меньше чем модуль Юнга, то коэффициент 0С1. При этом приполучим модель Б-2, конструкция лежащихся на основании

(6)

типа Винклера.

Характеристическое уравнение дифференциального уравнения (5) имеет вид

(7)

Корни характеристического уравнения комплексно-сопряжённыепри 0С1

,

, (8)

,

Общее решение однородного дифференциального уравнения (5) имеет вид

(9)

в зависимости от физико-механических свойств материала конструкции – С.

В частности, таблица №1

С
0
0,05	0,695	0,70694	-0,708	-0,707
0,09	0,685	0,706	-0,730	-0,7065
0,11	0,6804	-0,7063	-0,735	-0,7062
0,13	0,676	-0,7064	-0,741	-0,7059
0,14	0,673	-0,705	-0,743	-0,706
0,16	-0,670	0,7056	-0,747	0,7054
0,17	0,667	0,705	-0,752	-0,7055
0,18	0,664	0,7051	-0,754	0,7048
0,19	0,662	0,7049	-0,757	0,7045
0,2	0,660	0,7047	-0,7597	0,7042
0,3	-0,788	0,703	0,638	-0,7019
0,4	-0,8177	0,695	0,6176	-0,698
0,5	-0,848	0,686	0,598	-0,694
1,0	0,494	-0,654	-1,094	-0,54

Постоянные интегрирования однородного дифференциального уравнения определяются из граничных условии конкретной задачи.

Характеристическое уравнение дифференциального уравнения (6) имеет вид

(10)

Корни также комплексно-сопряженные (таблица №1 при). Следовательно, общее решение однородного дифференциального уравнения (6) имеет вид

,(11)

В качестве примера рассмотрим изгиб тонкостенной конструкции под действием ударного импульса в центре координат, когда сила контактного воздействия сосредоточенная под нагрузки, а конструкция шарнирно и скользящее закреплена на расстоянии – L.

1.1 Изгиб тонкостенной конструкции под действием ударного импульса в центре координат, когда сила контактного воздействия сосредоточенная под нагрузки, а конструкция шарнирно закреплена на расстоянии – L.

В данном случае, граничные условия есть

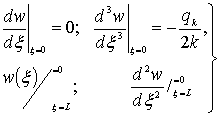(12)

общее решение

(13)

Подставляя (13) в граничные условия (12), определим произвольные интегрирования а затем их значения подставляя в общее решение (13) получим:

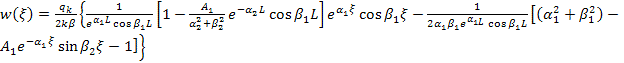, (14)

где, (15)

(16)

где , (17)

Уравнения (14) – (17) решены на ЭВМ при следующих данных:

: , , , ;

: , , , ;

;

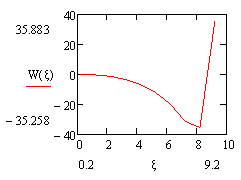
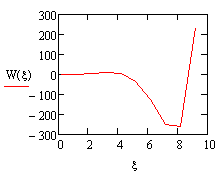
график 1, график 2

В частности,

В зоне области константа ударного импульса с конструкцией изгиб осуществляется по аналогии модели конструкции, лежащей на основании типа Винклера по формуле

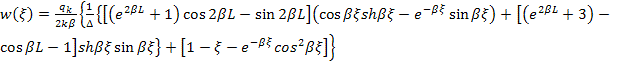, (19)

где ,, , (20)

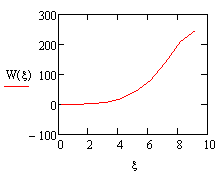
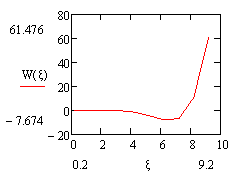
график 3

график 4

1.2 Изгиб тонкостенной конструкции под действием ударного импульса центре координат, когда сила контактного воздействия сосредоточенная под нагрузкой, а конструкция скользящее закреплена на расстоянии – L.

В данном случае, граничные условия есть

,

, , (21)

А общее решение

+

, (22)

Подставляя (22) в граничные условия (21), определим произвольные постоянные интегрирования а затем их значения подставляя в общее решение (22) получим:

(23)

где , (24)

Уравнения (23) – (24) решены на ЭВМ при следующих данных:

: , , , ;

; (25)

В частности

В зоне области константа ударного импульса с конструкцией изгиб осуществляется по аналогии модели конструкции, лежащей на основании типа Винклера по формуле

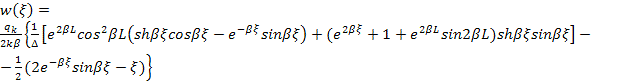,(26)

где,,.(27)

Выводы:

1) На графиках 1-4 приведены линии возможных микротрещинматериалови какое возможное разрушение вызывает ударный импульс при сдвигом деформировании площадки контакта.

2) Предварительное награждение поперечного сечения площади контакта (внутреннее критическое напряжение в долях 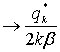) повещают коэффициент динамичности, а внешнее нагруженные наоборот уменьшает.

3) Существенное влияние на величину возмущения оказывает величина и степени комплексной податливости площади контакта

,

где - податливость, -релаксированный модуль упругости, комплексная жидкость,

4) Коэффициент потери энергии определяется 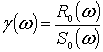где, - постоянный множитель силы внутреннего трения,-амплитуда упругого напряжения.

Литература

1. С.Н.Соколов, «Круглая пластинка на обобщенном упругом основании, Инженерник сборник», т. 2, 1952 г.

2. А.Р.Кер, «Упругие и вязкоупругие модели основании», «Прикладная механика», 1964 г.

3. Е.Т.Божанов, Ж.С.Ержанов, «Исследование проблем устойчивости упругих тел, гибких пластин и оболочек и их приложения», «Қазақстанжоғарғымектебі», Алматы 2001 г., 300с.

4. В.З.Партон, «Механика разрушения от теории к практике», Москва, Наука, 1990 г., 239с.