Физика/5.геофизика

Prof. B.D. Khristoforov.

Institute Dynamics of Geospheres RAS. Moscow. E-mail:khist@idg.chph.ras.ru

Dynamic viscosity of solids in ultra - wide range of the
deformations time

Introduction

Many rheological models of rocks and various materials are considered
viscosity coefficient η constant or a function of temperature. In our tests on the
loading by blasts and the impacts of porous rock salt, limestone, marble, textolyte was observed linear increase in viscosity in the range η = 10⁴ - 10⁹ Pas at deformation for the time τ = 10^-7 - 10^-2 sec [1,2]. These data were supplemented by values of η,
obtained with the comprehensive and axial compression of limestone on the press in the study of creep [3], from geophysical estimations of continental drift [4], after the lifting of the Scandinavian Peninsula from goes glacier of 9000 years ago [5] and the displacements of mascons on the bottom of the lunar seas [6]. At times the
deformation τ = 10^-7 - 10¹⁷ sec (up to 4,5 10⁹ years old) for the investigated materials was obtained linear empirical relation η ≈ Gτ, where G is close to the shear modulus. This relationship was confirmed by analysis of the generalized model for
multi-component solid of Fought and consistent with the model for highly viscous
liquids [7].

Below are the results of research the viscosity to a wider range of hard bodies. Rheological processes at motion of dislocations in crystals were considered. On 3 orders of magnitude increased times deformation, elastic modulus and external
pressures. The previous data and methods for determining viscosity were correct. The results may be useful in the construction of geophysical models and mathematical modeling of dynamic processes in the lithosphere and mantle using rheological
models [8, 9].

Analysis of experimental data

The values of the viscosity coefficient η were determined in a wide range of
deformation time τ for loads close to destroying under explosive and impact loading of various materials from literature and author data. Various methods of determine η were applied depending on the conditions of deformation. Viscosity at the nano scale ~ 10^-9 m and τ ~ 10 ^{- 10} - 10 ^{- 8} sec being determined by dynamic braking of
dislocations in crystals [11, 12] by the formulas

η = αB/b²N_m ; τ = B/2Gb²N_m (1)
where B = 0,001 – 0,01 Pasec - viscous braking coefficient of the dislocation,
b ≈ 0,2 – 0,3 nm and N_m ≈ 10⁹ m^-2 Burgers vector describing the displacement of the moving dislocations and its density per unit area, α < 1 - constant. Viscosity η = 30 and 50 in crystals Nacl at times of relaxation for dislocations τ = 1,3 and 1,9 nsec are presented in [11]. The coefficient viscosity of metals Al and Be in the elastoplastic region [12] are presented in Table 1. Coefficient of viscosity η defined by the relaxtion time of dislocations τ = B/2Gb²N_m. I am determined coefficient η₁ on time τ₁ rise of the shock front by the formula
η = τ²ρC³/5,8х (2)
where G, ρ, C, u - shear modulus, density, longitudinal sound velocity and mass
velocity substance.

Table 1. Results determine the viscosity at blast loading of Al and Be [12].

Materials	ρ, kg/m^3	P, MPa	G, MPa	τ, nsec	η, Pas	τ1, nsec	η1, Pas	Nm, 10^-10m^-2
АL	2700	1620	32000	6.6	420	250	16000	19
		3250	34000	1.5	100	31	2108	25
		8350	42000	0,6	50	6	504	40
Be	1800	5110	160000	0,41	130	30	9600	3,8
		9840	174000	0,53	185	23	7656	4,5
		15400	184000	0,39	150	11	4048	5,5
		24300	200000	0,18	70	4	1600	7

Table 2 shows the measurements η for rock and porous materials at blast
measurements, where n - the coefficient porosity, P - pressure, σ_s - crushing strength. At τ ~ 10 ^{- 7} - 10 ^{- 4} sec η usually determined by the formula (2) on the rise time τ measured at different distances x in the plane wave compression at blasts and shock. Shock waves with a smeared front were obtained in the phase transitions, elastic - plastic flow and porous materials. When τ > 10 ^{- 4} sec η values obtained at explosive field measurements from the formula (3), where σ external stress, dε/dt - rate of deformation.

η = σ/(dε/dt) = σ/(du/dx) (3)

Table 3 shows the estimates coefficient η from deformation characteristics rocks from [3 - 6].

Table 2. The coefficients viscosity of porous materials at loading by blasts or shocks.

Rocks	ρ, kg/m^3	C, km/s	σs, MPas	P, MPa	G, МПа	τ, 10^-6s	η, 10^4Pas
rock salt, n = 20 %	1730	3,09	22	200-600	5800	1,5-5,4	0,18-1,22
rock salt, n = 13 %	1880	3,61	39	280-710	8100	0,67-4,0	0,09-1,6
rock salt, n = 1,5 %	2130	4,41	92	330-600	13300	0,6-1,5	0,12-0,24
marble, n = 0,4 %	2700	4,3	50	940-2300	20500	0,3-3	0,11-14
limestone, n = 3%	2600	4,4	86	119-187	19600	750-4000	1100-5000
textolite , n = 18%	1340	2,61	150	200	2410	1,5-11	0,09-1,6
Sand, moisture content to 3 %	1500- 1600	0,10 -0,08	-	0,6-0,2	5,2	8600-13000	10 - 20

Table 3. Viscosity η of rocks at large times of deformation τ.

Rock	P, MPa	G, MPa	τ, sec	η, Pas
limestone ρ = 2700 кг/м^3[3]	400	20000	1,9 10^3-1,1 10^7	2,4 10^13-1,9 10^17
Scandinavian peninsula [5]	1000	20000	2,8 10^11	10^19-10^22
Rocks of Earth's crust [4]	500	20000	3,2 10^10-3,2 10^12	10^21-10^25
Cora of Moon, ρ =3400 кг/м^3 [6]	50-200	20000	3,2 10^10-1,4 10^17	10^20-10^29
Earthquakes М>7 [5]	-	45000	7,3 10^6; 0,95 10^8	3,2 10^17; 4,2 10^18

Tables1 - 3 shows the values of viscosity η at the times of deformation
τ ≈ 10^-10 - 10¹⁷ sec in materials, at where shear modulus differ by almost 4 orders of magnitude. Fig. 1 shows the dependence of η/G from t in logarithmic coordinates, which agrees well with their line approximating η/G = τ, for G = 20000 MPa for all data. Noticeable deviation of η/G at τ ≈ 10^-6 - 10^-5 sec from curve fitting due to the dependence of η from pressure and temperature of shock wave, with increasing which η decreases. The best agreement is observed for limestone and sand at the
lowest pressures and temperatures. For short times the deformation characteristic for the development of dislocation viscosity metals practically coincides with viscosity of rocks. Viscosities of metals usually lower than at rock at long times of deformation [11, 12].

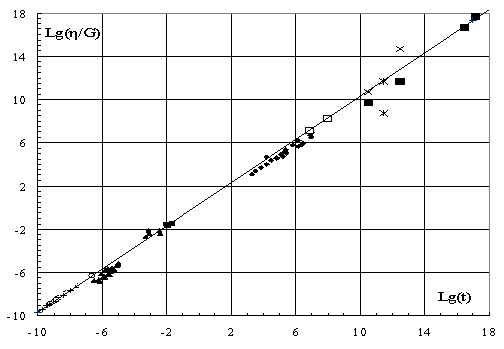
Fig. 1. Dependence η/G from t. Straight line - η/G = τ, at G = 20000 MPa. Direct crosses - Be, great circles Al, rhombis and small circles - marble and limestone, triangles NaCl, small squares - wet sand, rhombis limestone - [3], the stars - Scandinavian peninsula [5], oblique crosses - Earth's crust [4]. Large black squares - lunar rocks [6]. Transparent squares - earthquakes [5].

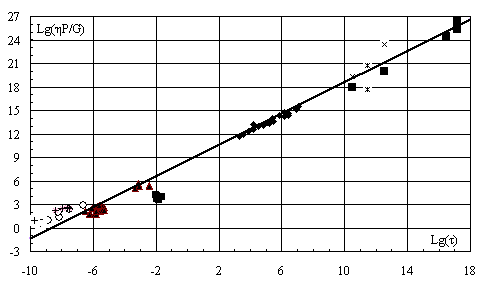
Fig.2. Dependence Lg(ηP/G), (Pas) from Lg (τ), (s) for all date. Legend is as at Figure 1.

Fig. 2 shows the dependence ηP/G from τ for all data. Blasting and shock point for metals lie above and the porous materials point lie below of averaging curve due to the higher temperature in them under a shock compression.

The discussion of results

The experimental data can be approximated by empirical formulas η/G = τ;
η = 4 10⁸(G/P)τ. Similar dependences are observed for viscous liquids and homogeneous materials. For inhomogeneous materials from the generalized model of Fought [2,7], in which time τ establishing strain ε under the tension σ for a slice from a large number of grains (with average values of η and G) increases with increasing viscosity can write

τ = η/G; dε/dt = σ/eη = σ/etG; η = σ/(dε/dt) = etG (4

This implies that the viscosity increases with the time of deformation, elastic modulus and strain rate decrease. This is consistent with the data shown in figures. In the dynamic experiments the viscosity decreases with increasing external load.
Simultaneously grown and strain rate. Apparently, the product of η (dε / dt) ≈ σ is
performed in the entire range of times the deformation at a constant temperature.

In the studied rocks and porous materials viscosity characterizes the dissipation of energy during dynamic deformation due to friction and moving grain. To obtain the dependence η(τ) - absorption coefficient is proportional to the frequency, which is consistent with the principle of geometric similarity. If the viscosity would not be proportional to the loading time, then its associated energy absorption coefficient would be proportional to the square of the frequency of the sound that would violate the law of geometric similarity in blasts.

If the tensors of stress σ_ik and strain u_ik depend on time through the factor e^-iωt, then σ_ik = 2Gu_ik/(1 + i/ωτ), where ω - the frequency of the external force and
τ - relaxation time [7]. When ωτ »1 we obtain the usual expression for the elastic bodies σ_ik=2Gu_ik and when ωτ «1, σ_ik = 2Gτ du_ik/dt = 2ηdu_ik/dt dependence for
liquids with a viscosity η = Gτ. In crystals this are dislocations. In continents are crustal blocks between faults. Probing body perturbations of different frequencies can be determined by their structure characteristic times of establishing equilibrium
deformation τ, where η = Gτ. Over the entire range from dislocations to continents general equation for determining the rheological rocks, porous materials and metals at nano - technologies associated with the common features of their structure may take the form σ_ik = 2ηdu_ik/dt.

Thus, when changes the structure and sizes of bodies, respectively, and changes the time of establishment of equilibrium deformation and strength characteristics of the material. This is consistent with the theory that the relaxation of the shear stress on irregularities leads to the dependence of mechanical properties on the strain rate [8, 10]. Therefore, to simulate the behavior of bodies at different strain rates can be applied very viscous liquids [7] type of rosin, when performed equations (4). Earlier the rosin were using for modeling of blasts processes in geomechanics [10].

This is due to the fact that the deformation processes occur at all levels of the
hierarchy of structure from crystals to continents [8 - 10]. Such a medium can behave as an elastic body at high frequency of the external load, the same medium behaves as a plastic body regardless of its size at low frequency load.

Conclusion.

It were a study of the rheological characteristics of solids in a wide range of times and speeds of deformation 10^-10 - 10¹⁷sek and 10¹⁰ - 10^-17sek^-1 at external loads 1-20000 MPa. The results of data processing of explosive laboratory and at field
experiments, studies of creep, estimates of continental drift, the lifting of the Scandinavian Peninsula glacier 9000 years ago, the recovery time surface at the epicenter of a strong earthquake displacements, mascon displacements at the bottom of the lunar maria, etc. It is shown that in the range of parameters the effective viscosity is proportional of the time of deformation, the elastic moduli and decreases with increasing pressure and velocity of deformation. Effective viscosity is generalized characteristic rheological behavior solids of size from the nanoparticles to the continent because the influence of their structure at different levels on deformity process.

References
1. Khristoforov B.D. Investigation of rock deformation and different materials while changing the strength, speed and time of deformation within a wide range. Physical fields and the dynamics of
interacting geospheres. IDG RAS. Moscow. 2007. P. 123 - 129.

2. Khristoforov B.D. Experimental modeling of impact of space dust and debrison flying vehicles and their components. Cosmic research, 2011, Vol. 49, No.3. P. 263–268.

3. Ryabinin Yu.N., Beresnev B.I., Martinov E.D. Mechanical properties and processes in solids
under high pressure//Journal of geophysical research. 1971. Vol.76. No5. P.1370 - 1375.
4. Goldin S. Destruction of the lithosphere and physical mesomechanics // Physical mesomechanics. Novosibirsk. 2002. 5 (5). P. 5 - 22.

5. Magnitsky V.A. Internal structure and physics of Earthi. Moscow. Nedra. 1965. 379 p.
6. Gilvary J.J. Internal temperature of the Moon // Nature.1969. Dec. 6224. № 5223. P. 968 – 970.
7. Landau L.D., Lifshitz E.M. Theory of elasticity. Moscow. Nauka. GRFML. 1985. 204 p.

8. Sadovsky M.A., Bolhovitinov L.G., Pisarenko V.F. Deformation of geophysical environment and seismic processes. Moscow. Nauka. 1987. 100 p.

9. Nicholaevsky V.N. Elastic - viscous models of tectonic and seismic waves in the lithosphere // Physics of the Earth. Moscow. 2008. No 12. P. 92 - 96.
10. Rodionov V.N., Sizov I.A., Tsvetkov V.M. Basics mechanics of rocks. Moscow. Nauka. 1986. 301 p.

11. Alshin V.I., Indevom V.L. Dynamic braking of dislocations//Progress physical science.
Moscow. 1975. Vol.115 No 1. P. 48 - 84.

12. Ogorodnikov V.A., Tyunkin E.S., Ivanov A.G. Strength and viscosity of metals in a wide range of strain rate // Journal applied mechanics and technical physics. Novosibirsk 1995. Vol. 36. No 3. P. 134 - 140.