к.т.н. Шмидт И.В., д.т.н. Дьяконов А.А.

Южно-Уральский государственный университет, Россия

Постановка задачи теплопроводности

в цикле круглого шлифования

Одним из основных методов обработки при обеспечении точности и качества поверхности является шлифование. Обработка на шлифовальных станках осуществляется по определённому циклу, позволяющему адаптировать производство детали к различным технологическим условиям.

Процесс абразивной обработки является теплонапряженным и сопровождается выделением большого количества тепла в зоне обработки, что нередко приводит к образования различных тепловых дефектов. Поэтому одним из главных ограничивающих критериев при проектировании циклов шлифования является температура в зоне шлифования – предельная прижоговая температура.

Поскольку при расчете бесприжоговых режимов резания критерием является предельная температура в зоне шлифования, то необходимо определить на какой поверхности по глубине поверхностного слоя заготовки рассматривать предельную температуру.

Принятие в качестве критериальной точки на обрабатываемой поверхности на каждом рабочем ходе приведет к работе на заниженных режимах резания, тем самым к снижению производительности процесса. К такому же результату приводит и использование в качестве критерия предельной температуры на поверхности готовой детали. Реально схема снятия припуска с заготовки за цикл шлифования выглядит, как показано на рис. 1. Поэтому более эффективное решение задачи, когда предельную температуру относят к поверхности готовой детали [1]. На самом деле важно, чтобы поверхностный слой готовой детали остался бездефектным.

На первом рабочем ходе на обрабатываемую поверхность выделяется количество тепла, соответствующее принятой подаче, и надо, чтобы температура на границе снимаемого припуска и готовой деталью не превышала предельную (см. рис. 1). Необходимо задать такое количество тепла (скорость радиальной подачи Vs_рад) чтобы температура на поверхности готовой детали не превысила предельную. Но на втором обороте расстояние до готовой детали уменьшилось (уменьшилась величина снимаемого припуска П), следовательно, интенсивность теплового потока Q’ необходимо уменьшить, т.е. пересчитать скорость радиальной подачи Vs_рад для этого оборота заготовки. И так на каждом обороте детали. Тогда актуальной становится задача нахождения закона изменения скорости радиальной подачи Vs_рад от времени, или от номера оборота детали, что будет являться эффективным циклом шлифования.

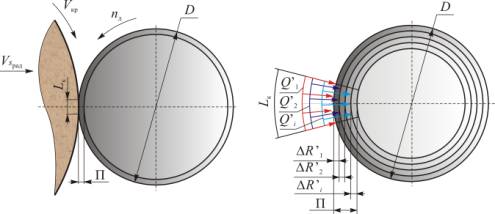
Рис. 1 – Схема снятия припуска при многопроходной обработке
(Vs_рад – скорость радиальной подачи, мм/мин; V_кр – скорость круга, м/с; n_д – скорость вращения детали, мин^-1; D – диаметр заготовки, мм; L_к – длина дуги контакта, мм; П – припуск на обработку, мм; ΔR’₁, ΔR’₂, ΔR’_i – глубина резания на первом, втором, i-ом обороте заготовки, мм; Q’₁, Q’₂, Q’_i – интенсивность теплового источника на первом, втором, i-ом обороте заготовки, Вт/м)

Такой подход к формированию эффективного цикла обработки учитывается в теплофизической модели процесса круглого шлифования с радиальной подачей.

Рассмотрим круг радиуса R, теплоемкости c на единицу объема, дж/(мм³·К); теплопроводностью q, дж/(мм·с·К). Круг представляет собой цилиндр единичной высоты с теплоизолированными торцами.

Поскольку в процессе обработки с поверхности заготовки снимается припуск равный двойной глубине резания на каждом обороте заготовки, то в каждый момент времени действительный размер круга равен R + ∆R’, где ∆R’ – глубина резания.

На круг действует тепловой источник мощностью Q’, Дж/мм²·с·К при прохождении точки на поверхности круга зоны резания (дуги контакта) с угловой скоростью ω’, рад/с. За пределами действия теплового источника с обрабатываемой поверхности происходит теплоотдача с коэффициентом μ’, Дж/м²·с·К, внутри круга – с коэффициентом ν’, Дж/мм³·с·К.

Получаем двумерную постановку задачи теплофизики с расчетной схемой, представленной на рис. 2.

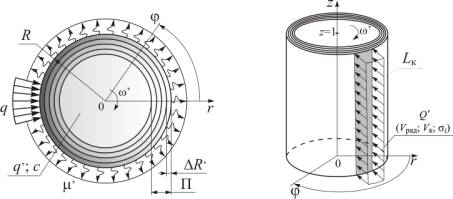
Рис. 2. Расчетная схема

Уравнение теплопроводности для данной схемы примет вид:

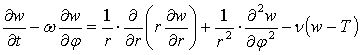, (1)

где w=w(r’, τ) – температура, град.; ; r’ – расстояние от центра круга, мм; τ – время, с; ; , мм²/с; φ – угол в неподвижной системе координат; ; T – температура окружающей среды, град.

Начальные условия: температура принимается равной температуре окружающей среды:

, (2)

где r – полярный радиус (r≤1); φ – полярный угол.

Краевые условия:

, (3)

где ; ; .

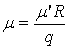Таким образом, в двумерной схеме получаем задачу в виде уравнения теплопроводности и совокупности краевых условий второго и третьего рода, т.е. смешанную краевую задачу для уравнения (1).

Работа выполнена при финансовой поддержке Гранта Президента РФ № МК-873.20014.8.

Литература:

1. Анельчик, Д.Е. Циклы бездефектной обработки на шлифовальных станках / Д.Е. Анельчик //Металлорежущие станки; Респ. межвед. науч.-техн. сб. – 1989. – Вып. 17. – С. 68–71.