Отраслевое машиностроение-3

Корчак Н.Н.

Андреев А.А.

Подольский государственный аграрно-технический университет

Вычисление сил сопротивления рабочих почвообрабатывающих органов при их движении в почве

Все существующие почвообрабатывающие рабочие органы выполняют функциональные объязаности в процессе своего движения. Имея конечные размеры и самые различные геометрические формы, они неизбежно подвержены действию сил сопротивления со стороны почвы, что приводит, во-первых, к изменению характера движения и, во-вторых к диссипации энергии. В предлагаемой работе рассматриваются вопросы, связанные с вычислением сил сопротивления.

Моделируем почву средой с вязкостью η. Среда является однородной по высоте обрабатываемого слоя (предполагается, что глубина обрабатываемого слоя намного больше всех других, встречающихся в дальнейшем рассмотрении размеров). Рабочий орган без потери общности может быть смоделирован упругим, вертикальным цилиндрическим стержнем (нулевая модель). В процессе своего поступательного движения в почве он возбуждается в следствии возникновения фрикционных автоколебаний, которые являются высокочастотными, поперечными относительно оси стержня и осуществляются в плоскости поступательного движения (предполагается, что стержень имеет продольную плоскость симметрии, чем исключаются из рассмотрения изгибно-крутильные колебания). Вихри Кармана являются низкочастотными и возбуждают поперечные вынужденные колебания как относительно оси стержня, так и относительно направлению движения. Затухание колебаний Кармана гораздо слабее, чем вынужденных фрикционных автоколебаний.

Действительно:

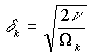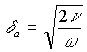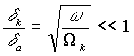; ; (1)

Здесь ν – кинематическая вязкость почвы;

δ – глубина проникновения;

ω и Ω_k – частоты фрикционных установившихся автоколебаний и колебаний Кармана (рис.1).

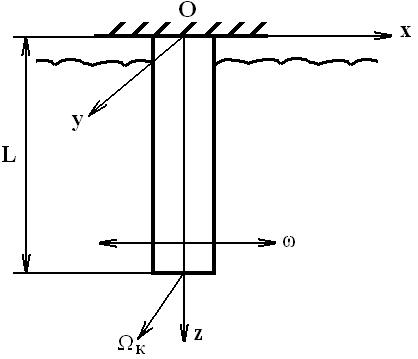
Рис. 1. Схематическое изображение цилиндрической консоли для вычисления силы трения

Более точный анализ требовал бы рассмотрения суммарного колебания, траекторией каждой точки которого является фигура Лиссажу. При сделанных предположениях уравнение Навье-Стокса превращается в уравнение типа одномерного уравнения теплопроводности [2]:

(2)

Решение, удовлетворяющее условию V=U при x=0:

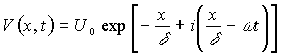(3)

где - скорость колебания цилиндра.

Полная диссипируемая в единицу времени энергия равна:

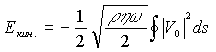(4)

где - интеграл, взят по всей поверхности колеблющегося тела;

ρ – плотность почвы;

Вычисления показывают, что диссипация энергии связана только с вещественной частью Е_кин. Эту часть силы сопротивления называют диссипативной.

Для цилиндра радиусом R (R>>δ) распределение скорости обтекаемой в поперечном направлении почвы даётся выражением:

(5)

где - внешняя нормаль к цилиндрической поверхности. Отсюда можно получить тангенциальную скорость на поверхности цилиндра:

(6)

Для получения (6) введены полярные координаты в поперечном сечении цилиндра. Несложные вычисления (4) с учётом (6) дают:

(7)

Это выражение для диссипативной части энергии позволит определить погонную силу сопротивления:

(8)

Безусловно, учёт конкретной геометрической формы рабочего органа, учёт зависимости u(z), которая следует из решения задачи [3] о поперечных колебаниях консоли, других неучтённых эффектов, значительно усложняет расчёт силы трения (модели более высоких уравнений). Следует отметить также, что большое различие кармановской частоты и ω позволяет рассматривать “расцеплённые”, независимые уравнения.

Литература:

1. Lamb H. Hydrodynamics. – Cambridge, 1932

2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Гидродинамика, т. 6. – М., Наука, 1988;

3. Бидерман В. Л. Прикладная теория механических колебаний. – М., Высшая школа, 1972.