О минимальных фигурных комплексах

О минимальных фигурных комплексах

к.ф.-м.н. доц. В.И. Евсеев

Казанский (Приволжский) федеральный университет,

Казань, Россия, кафедра прикладной информатики

УДК 681.32

1. Логические фигуры.

Логические фигуры представляют собой соединенные в определенной последовательности (склеенные) квадратные клетки одного размера. По количеству, которые содержат фигуры, мы будем их подразделять на следующие виды:

– 1 клеточные фигуры (униады) 2 набора по 2 фигуры,

– 2 клеточные фигуры (диады) 2 набора по 2 фигуры,

– 3 клеточные фигуры (триады), 4 набора по 2 фигуры.

– 4 клеточные фигуры (квадриады), 2 набора по 5 фигур,

– 5 клеточные фигуры (пентимы), 2 набора , 12 фигур,

– 6 клеточные фигуры (гексимы) , 1 набор, 35 фигур,

– 7 клеточные фигуры (септимы), 1 набор, 112 фигур.

Фигуры больших размерностей нами еще не изучены.

Одно, двух и трех клеточные фигуры с читаются малыми, четырех и пяти клеточные – средними, шести и семи клеточные – большими. Комплексы состоят из различных сочетаний фигур, взятых из указанных наборов.

Все фигуры располагаются на прямоугольном поле, которое мы будем называть полигоном. Рассматриваемые на полигоне фигуры назовем фигурным комплексом, при этом обычно указывается его фигурное содержание с указанием видом фигур и их количества по этим видам.

2. Основные виды полигонов.

Полигон по своей сути представляет собой прямоугольную матрицу, расположенную на плоскости. Конечно, можно рассматривать и пространственные полигоны, но это требует специальных методов, такие полигоны будут нами изучены в будущем. Целью настоящих заметок является – познакомить читателей с методами фигурного логического анализа на самых простых моделях полигонов.

Полигон мы будем обозначать греческой заглавной буквой с указанием в скобках типа той матрицы. Простейшим полигоном умы считаем следующий:

, который содержит три строки и четыре столбца:

В дальнейшем мы будем предполагать фиксацию расположения полигона на плоскости, указанную в наименовании. Полигон называется полным, или правильно покрытым, если на каждой его клетке расположена некоторая клетка некоторой фигуры, аналогично и фигурный комплекс называется полным, если он полностью покрывает заданный полигон. Напомним, что само покрытие называется правильным, если все расположенные на полигоне фигуры полностью покрывают его и не имеют пересечений. В данной статье мы будем рассматривать только правильные покрытия уже построенного полигона . Полигон может допускать усечение, когда из него исключаются некоторые клетки. Обычно это бывают угловые диагональные клетки, например, на построенном полигоне возможно исключение верхней правой диагональной клетки, что отмечается жирной точкой в виде левого верхнего индекса в обозначении полигона . У этого полигона 11 рабочих клеток. Также можно исключить две клетки – края главной диагонали, тогда получится полигон . Если исключаются какие-то произвольные клетки, то они указываются в фигурных скобках после обозначения полигона.

3. Виды малых фигурных комплексов

Мы будем обозначать фигурные комплексы латинской буквой с указанием в квадратных скобках типов фигур и их количества.

Рассмотрим основные случаи построения малых фигурных комплексов на минимальном полигоне.

По количеству типов фигур комплексы могут однотипные, двухтипные и т.д.

Рассмотрим основные частные случаи на этом полигоне.

1. Однотипные комплексы.

1.1. Фигурный комплекс .

1.2. Фигурный комплекс .

2. Двухтипные комплексы.

2.1. Фигурный комплекс .

2.2. Фигурный комплекс .

3. Трехтипные фигурные комплексы.

3.1. Фигурный комплекс .

Остальные возможности требуют большей размерности исходного полигона, и мы их рассмотрим в своих последующих работах. Конечно, возможны и другие сочетания фигур, здесь приведены наиболее популярные, которые мы постепенно будем рассматривать в цикле предполагаемых статей, а в дальнейшем, возможно, а в монографии по этой теме, когда будет накоплен достаточный для этого объем материала.

4. Расположение фигур на полигоне.

Уравнения фигур зависят от их расположения. При этом нужно учитывать принятую за исходную позицию фигуры, ее симметрии, а также реальный вид, полученный с помощью преобразований из этого исходного вида. Мы будем применять два основных вида преобразований фигур: повороты на (против часовой стрелки) и зеркальную симметрию фигуры . Таким образом, в общем случае возможны восемь различных случаев расположения, которые мы обозначим малыми буквами латинского алфавита, При этом первые четыре буквы (a, b, c, d) характеризуют исходную позицию фигуры, которая строго фиксирована, и ее пошаговые повороты.

Буквы с пятой по восьмую (e, f, g, h) определяют соответственно позицию исходной фигуры после ее зеркальной симметрии и последующие повороты фигуры, уже подвергшейся симметрии. Наличие симметрий уменьшает число возможных позиций фигуры на полигоне, но их число всегда четное (2, 4, 8). При этом, естественно, изменяются и логические формулы этих фигур.

5. Позиции и формулы триад.

Триады являются малыми логическими фигурами. Их всего две, поэтому у нас есть возможность сразу рассмотреть их позиции и соответствующие формулы. Начнем изложение с одноклеточной фигуры . Ее изображение не зависит от позиции:

Хотелось бы сделать предварительное замечание, что ей соответствуют бинарные логические операции первой группы (уровня), которые описаны в монографии автора [2], стр. 14, табл. 1.

Двухклеточная фигура имеет две основные позиции – горизонтальную:

(а)

и вертикальную:

(b)

Фигура . Она исходно предполагается расположенной горизонтально.

Этот вид изображается схемой:

(а)

Фигура . Она получается из исходной поворотом на против часовой стрелки:

(b)

Фигура имеет диагональную симметрию, поэтому у нее четыре различных позиции. Перечислим их.

Фигура . Она имеет исходную позицию

(а)

При повороте на получаем следующую позицию

(b)

При следующем повороте имеем

(с)

Последний поворот приводит к результату:

(d)

Теперь опишем формулы этих фигур с учетом их реальных позиций.

Построение логической формулы фигуры начинается с создания основного элемента – зерна, определенного фигурой и прямоугольной рамки, состоящей их нулевых элементов. Так, для униады получаем реальную формулу матрицы:

0	0	0
0	1	0
0	0	0

Здесь «1» в центре характеризует саму фигуру (зерно, состоящее из одной клетки), а кайма представляет собой прямоугольную рамку, содержащую только нули. Поэтому находится ее логическая матрица


	0	1	0
0	0	0	0
1	0	1	0
0	0	0	0

Сразу же получается логическая формула для этой фигуры

Аналогично, для диады находим две формулы, соответствующие ее возможным позициям. В случае горизонтальной позиции строится сначала матричная форма с двумя зернами и каймой:

0	0	0	0
0	1	1	0
0	0	0	0

Затем конструируется логическая матрица горизонтальной диады:



	0	1	0	1
0	0	0	0	0
1	0	1	1	0
0	0	0	0	0

Значит, формула этой диады такова

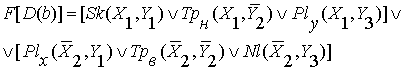
Таким же методом строится формула второго типа диады в случае ее вертикального расположения.

Поэтому мы ограничимся только результирующей формулой:

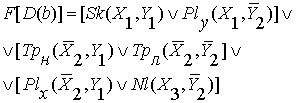
Теперь перейдем к формулам триад.




	0	1	0	1	0
0	0	0	0	0	0
1	0	1	1	1	0
0	0	0	0	0	0

Для фигуры получаем матрицу, позволяющую построить ее формулу.

Значит, получаем формулу этой фигуры:

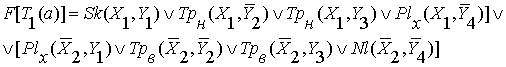Последующие строки заполнены нулями, что соответствует общей лжи , мы не будем указывать их в матрице и самой формуле.

В случае вертикального расположения этой фигуры ее матрица принимает следующий вид


	0	1	0
0	0	0	0
1	0	1	0
0	0	1	0
1	0	1	0
0	0	0	0

Значит, ее формула:

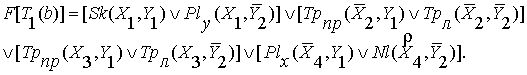
Аналогично, для исходной позиции второй фигуры получим матрицу



	0	1	0	1
0	0	0	0	0
1	0	1	1	0
0	0	1	0	0
1	0	0	0	0

Так находится формула этой фигуры:

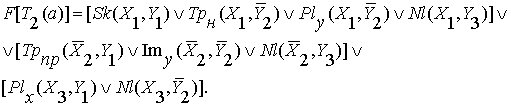
Вторая позиция этой фигуры характеризуется матрицей



	0	1	0	1
0	0	0	0	0
1	0	1	0	0
0	0	1	1	0
1	0	0	0	0

Поэтому ее формула такова:

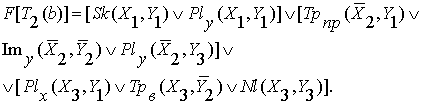
Матрица третьей позиции второй фигуры имеет вид


	0	1	0
0	0	1	0
1	1	1	0
0	0	0	0

Следовательно, формула этой фигуры:

Четвертая позиция этой фигуры определяется матрицей


	0	1	0
0	1	1	0
1	0	1	0
0	0	0	0

Так находится формула этой фигуры:

6. Полигон однотипного комплекса триад.

В качестве вывода по этим схемам строим уравнение самого комплекса триад . Его полигон имеет вид:

Надо сказать, что здесь имеется несколько вариантов решения, поэтому в каждом случае вид комплекса и его формула будут как-то различаться. Такие дополнительные решения мы будем называть изотопами фигурного комплекса.

Для построения формулы этого комплекса, отметим, что

Теперь остается подставить полученные формулы для самих фигур в формулу комплекса.

[].

Можно сделать вывод, что для любой возможной композиции фигур, составляющих некоторый комплекс, находится определяемая таким способом формула.

В качестве обобщения полученных результатов укажем на возможность применения «универсальных структурных матриц» размерности ( , которые отражают структуру логической формулы в каждом случае. Так, для униады получаем матрицу размерности (3,3), которая имеет вид:

Для горизонтальной диады структурная матрица имеет размерность (3,4):

Вертикальная диада имеет структурную матрицу размерности (4,3) :

7. Позиции и формулы квадриад.

Квадриады состоят из четырех исходных клеток, из всего 5 фигур. Нас будет интересовать логическая основа этой игровой структуры.

Сначала найдем все возможные позиции каждой из квадриад. Первая из фигур имеет исходное вертикальное расположение, а так как у нее две оси симметрии, то она имеет только две позиции:

а) вертикальная позиция

b) горизонтальная позиция

Вторая фигура квадриад не имеет никаких симметрий, поэтому у нее восемь различных позиций. Первые четыре из них получаются как исходная и ее повороты на .